Общие сведения. Наряду с сериальными закономерностями в спектрах существуют определенные закономерности и в распределении интенсивностей между спектральными линиями

Наряду с сериальными закономерностями в спектрах существуют определенные закономерности и в распределении интенсивностей между спектральными линиями дублетной, триплетной и в общем случае мультиплетной структуры. Эти закономерности также объясняются законами квантовой механики.

Под интенсивностью 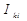спектральной линии, соответствующей переходам между уровнями k и i, понимается мощность излучения, пропорциональная излучению единицы объема источника

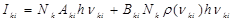, (1)

где 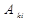– вероятность спонтанных переходов; 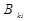– вероятность индуцированных переходов; 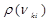– плотность излучения, отнесенная к единичному интервалу частот. В случае свечения газового разряда (за исключением лазеров) индуцированные переходы не играют существенной роли, поэтому, пренебрегая индуцированным излучением, при условии, что явления самопоглощения и диффузии (рассеяния) излучения в пределах излучающего объема отсутствуют, для интенсивности спектральных линий имеем

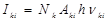. (2)

Следует отметить, что в газовых лазерах, наоборот, индуцированные переходы играют доминирующую роль, поэтому спонтанное излучение можно не учитывать.

В квантовых системах закон распределения частиц по энергиям имеет вид

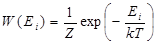, (3)

где нормирующая постоянная 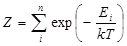(суммирование производится по всем состояниям); 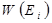– вероятность того, что какой- либо атом находится на энергетическом уровне 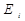. При постоянной температуре в активной излучающей среде устанавливается определенное распределение частиц по энергетическим уровням. При термодинамическом равновесии это распределение возникает и поддерживается как результат взаимодействия вещества с полем теплового излучения. Число частиц в единице объема среды, одновременно имеющих одну и ту же внутреннюю энергию, т. е. находящихся в одном из состояний, соответствующих данному энергетическому уровню, называется населенностью энергетического уровня. Населенности энергетических уровней определяются распределением Больцмана. Для простых невырожденных энергетических уровней распределение Больцмана имеет вид

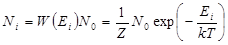. (4)

В этой форме распределение Больцмана наиболее часто встречается в литературе. Если в квантовой системе существует несколько вырожденных энергетических уровней, то в таком, более общем, случае распределение частиц по энергиям незначительно видоизменяется. Поскольку каждый вырожденный энергетический уровень представляет собой несколько «слившихся» невырожденных уровней, то вероятность 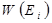и населенность 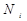вырожденных уровней должны быть пропорциональны числу совмещенных простых уровней, т. е. статистическому весу 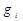(степени или кратности вырождения) данного энергетического уровня. В этом случае формула (3) приобретает вид

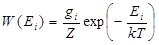, (5)

где

.

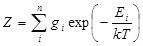В общем случае распределение частиц по энергетическим уровням описывается функцией

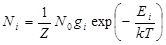. (6)

Сумма населенностей всех энергетических уровней равна коли­честву частиц N₀ в рассматриваемом ансамбле. В соответствии с рас­пределением Больцмана в основном состоянии с энергией E₁ при термодинамическом равновесии находится наибольшее число частиц (атомов, молекул), а населенности верхних возбужденных энергети­ческих уровней уменьшаются с ростом энергии уровня E_i; по экспо­ненте.

Отношение населенностей двух уровней в состоянии термоди­намического равновесия определяется следующим выражением:

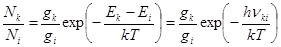. (7)

Для простых невырожденных уровней, т.е. когда 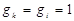, соотношение (7) принимает более простую форму:

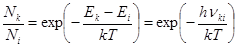. (8)

Равновесие системы является динамическим, в ней непрерывно происходят переходы с выделением и поглощением энергии. Поглощая энергию, частицы переходят из основного состояния в одно из возбужденных. Через некоторый промежуток времени частица самопроизвольно под действием внутренних возмущений возвраща­ется в основное состояние. Среднее время нахождения частицы в возбужденном состоянии называется временем жизни т. Для боль­шинства возбужденных состояний время жизни составляет 10^-6 – 10^-9с. Возбужденные состояния с большим временем жизни (10^-3 – 1с и более) называют метастабильными. Время жизни частицы в метастабильном состоянии значительно больше, чем частиц с другими возбужденными уровнями, т. е. при возбуждении квантовой системы на метастабильных уровнях происходит «накопление» частиц, иначе говоря, возможно увеличение населенности сверх равновесной. Изолированная система частиц, находящаяся в любом состоянии, отличающемся от распределения Больцмана для данной температуры, неравновесна. Такая система путем перераспределения энергии самопроизвольно перейдет в новое состояние термодинамического равновесия. Процесс перехода системы в состояние равновесия называется релаксационным.

Для многих квантовых систем процесс релаксации можно описать затухающей экспоненциальной функцией 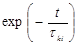. Постоянная времени затухания 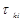называется временем релаксации между уровнями E_k и E_i. Если релаксация частиц с уровня k происходит одновременно на несколько уровней или под действием нескольких различных причин и отдельные составляющие релаксационного процесса не зависят друг от друга, то общую постоянную релак­сации 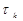для уровня k можно выразить через постоянные t_1, t₂, …, t_n, характеризующие различные релаксационные процессы, одновременно протекающие в системе

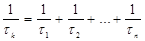. (9)

Общий релаксационный процесс может быть количественно охарактеризован экспоненциальным множителем вида 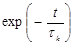. В оптическом диапазоне частот основным механизмом релаксации являются столкновения и cамопроизвольные (спонтанные) переходы. Сопоставляя найденные из опыта интенсивности спектральных линий, характеризующих то или иное состояние, с законом равновесного распределения (7), можно проверить факт выполнения условия термического равновесия в системе или обнаружить случаи отклонения от равновесия.

С учетом выражения (6) для интенсивности спектральных линий имеем

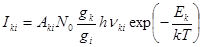. (10)

Отношение интенсивностей двух спектральных линий, возникающих при переходах k ® i, l® m,

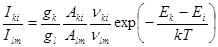. (11)

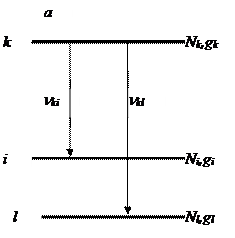
Отношение интенсивностей двух спектральных линий с общим верхним уровнем, возникающим при переходах k ® i, k ® l (рис. 1, а) дается выражением

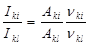. (12)

В этом случае отношение интенсивностей определяется лишь отношением атомных постоянных (вероятностей переходов) и частот линий. Заменяя 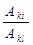через отношение сил осцилляторов 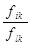или эйнштейновских коэффициентов , по формулам

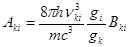; (13)

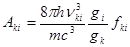(14)

выражение (2) можно представить в виде

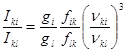и 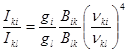, (15)

где g_i и g_k статистический вес соответственно i-го и l-го энергетических уровней.

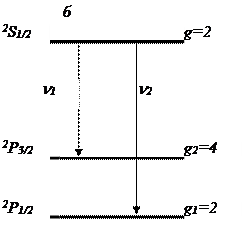
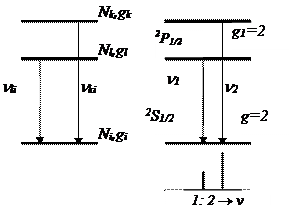
Примером соотношения указанного вида может служить выражение для отношения интенсивностей спектральных линий сериального дублета резкой серии щелочных элементов. Сериальный дублет резкой серии (рис. 1, б)

n = n p ²P_1/2,3/2 – n' s ²S_1/2

имеет простой верхний уровень ²S_1/2 и двойной нижний уровень ²P_1/2 и ²P_3/2. Для достаточно узкого дублета . Тогда

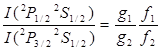. (16)

По данным измерений аномальной дисперсии, для таких дублетов f₁/f₂= 1. Принимая во внимание, что при отсутствии вырождения 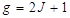, получим

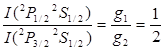. (17)

Таким образом, для ²P_1/2,3/2 ²S_1/2 интенсивности его компонент относятся как статистические веса дублетного уровня.

Для широкого дублета надо принимать во внимание зависимость от частоты n и пользоваться формулой (2). Сравнение формул (5) и (7) показывает, что для узких дублетов вероятности спонтанных переходов ²S_1/2 ® ²P_1/2 и ²S_1/2 ® ²P_3/2 относятся как А₁: А₂ = g₁: g₂ = 1: 2. В силу этого соотношения в дублетах второй побочной серии длинноволновая компонента вдвое интенсивнее коротковолновой.

		Рис. 2. Схемы уровней для двух спектральных линий с общим нижним уровнем (а) и уровней дублета главной серии Na I (б)
			Рис. 3. Схемы уровней энергии диффузной серии дублетов

Случай двух спектральных линий с общим нижним уровнем, возникающим при переходах k ® i и l ® i, отражен на рис. 2, а. Отношение интенсивностей спектральных линий равно

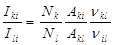, (18)

или

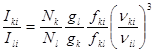. (19)

В данном случае отношение интенсивностей определяется не только отношением вероятностей переходов (или сил осцилляторов) и частот линий, но и отношением концентраций атомов на верхних уровнях 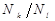. В зависимости от условий возбуждения заселенность верхних уровней может оказаться различной, поэтому отношение 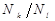может принимать различные значения. Следовательно, никаких общих выводов об отношении интенсивности этих линий сделать нельзя. Лишь в частном случае равновесного заселения уровней k и l по закону Больцмана

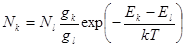, (20)

и формула (19) примет вид

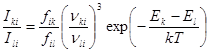. (21)

Рассмотрим отношение интенсивностей спектральных линий дублета главной серии щелочных элементов (рис. 2, б). Сериальный дублет главной серии

n = n s ²S_1/2 – n' p ²P_1/2,3/2.

Для достаточно узкого дублета приближенно

n_ki : n_li » 1, .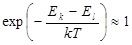

Следовательно,

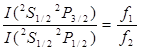. (22)

По измерениям аномальной дисперсии для дублетов главной серии отношение f₁ : f₂ » 2:1, откуда

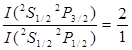. (23)

В данном случае отношение интенсивностей составляющих дублета равно отношению статистических весов дублетного уровня. В силу соотношения (13) в дублетах главной серии коротковолновая компонента вдвое интенсивнее длинноволновой.

Между двумя рассмотренными случаями (дублеты с общим верхним и общим нижним уровнями) имеется существенное различие. Для дублета с общим верхним уровнем пропорциональность отношения интенсивностей его компонент отношению статистических весов определяется лишь законами внутриатомных процессов и, следовательно, не зависит от условий возбуждения. Для дублета же с общим нижним уровнем отношение интенсивностей его компонент зависит от условий возбуждения. Оно равно отношению статистических весов лишь при равновесном распределении атомов по уровням, т. е. при равновесном тепловом возбуждении.

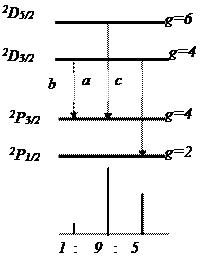
Правило интенсивностей обобщается также для случая, когда и начальные и конечные уровни сложные. Рассмотрим отношение интенсивностей спектральных линий первой побочной (диффузной) серии дублетов (рис. З): нижние уровни ³P_1/2,3/2 имеют статистический вес 2 и 4, верхние уровни ³D_3/2,5/2 – 4 и 6. В силу правила отбора при переходах между уровнями возникают три линии - a, b, c, интенсивности которых I(а) :I(b):I(c) = 9 : 1 : 5.

Если линии возникают при комбинировании между двумя сложными уровнями, то суммарные интенсивности линий при слиянии верхних (или нижних) уровней в один общий относятся как статистические веса соответствующих нижних (или верхних) уровней (правило сумм Доргело-Бюргера).

В общем случае для мультиплетов относительные интенсивности линий определяются через квантовые числа L, S и J по приведенным формулам.

Переход L ® L:

;

;

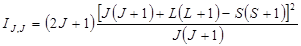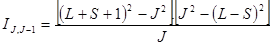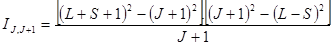
Переход L ® L-1

;

;

.

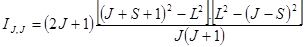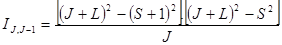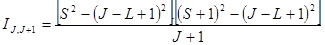Формулы справедливы для случая нормальной [L - S]-связи между моментами для узких мультиплетов при равновесной заселенности верхних уровней.