Общие сведения. Одна из важнейших закономерностей строения атомных спектров – их сериальная структура

Одна из важнейших закономерностей строения атомных спектров – их сериальная структура. Сериальные закономерности представляют собой яркое проявление квантовых свойств излучающих атомных систем. Линии линейчатого спектра атомов газа, находящегося при низком давлении, могут быть объединены в определенные, закономерно построенные группы – так называемые серии. Длины волн всех линий, принадлежащих к одной и той же серии, связаны между собой. Сериальные закономерности в наиболее простой форме проявляются в спектре одноэлектронного атома водорода, для которого они и были открыты впервые.

Рассмотрим атом водорода и сходные с ним ионы (модель так называемого водородоподобного атома), т. е. предположим, что имеется атомная система, состоящая из ядра с зарядом Ze и одного электрона с зарядом – е, где Z – порядковый номер элемента в периодической системе.

Кулоновская сила f взаимодействия между ядром и электроном играет роль центростремительной силы, равной для круговой орбиты

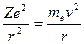, (1)

где 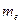- масса электрона; r – радиус орбиты.

В электрическом поле ядра электрон обладает потенциальной энергией

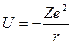. (2)

Полная энергия электрона равна сумме потенциальной и кинети­ческой энергий. С учетом (1) и (2) и знаков в этих выражениях

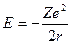. (3)

Согласно представлениям классической электромагнитной тео­рии, вращающийся по орбите электрон возбуждает вокруг себя пе­ременное электромагнитное поле, распространяющееся в простран­стве со скоростью света. Иначе говоря, ускоренно движущийся электрон при своем движении вокруг ядра должен излучать и вслед­ствие этого терять часть энергии. Таким образом, согласно клас­сической механике, энергия электрона все время уменьшается. Из формулы (3) следует, что меньшему значению энергии (с учетом зна­ка) соответствует меньший радиус. В результате электрон должен «упасть» на ядро. Из формулы (1) следует, что с уменьшением радиу­са орбиты скорость движения электрона возрастает, т. е. период обращения уменьшается. Это должно привести к непрерывному уве­личению частоты излучаемых электромагнитных волн, и атом дол­жен излучать непрерывный (сплошной) спектр. Однако в действитель­ности атом – устойчивая система и может излучать лишь линейча­тый спектр. Выход из создавшегося противоречивого положения был предложен Бором.

Теория водородоподобного атома. Основываясь на гипотезе Планка о квантовом характере излучения и поглощения, Бор сфор­мулировал законы, описывающие состояние и движение электронов в атоме в виде определенных постулатов, которые дают объяснение экспериментальным данным. Постулаты эти таковы.

1. Электрон в атоме может вращаться только по строго опреде­ленным стационарным орбитам, радиусы которых определяются из условия

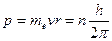, (4)

где p – момент импульса электрона; n – главное квантовое число, принимающее целые положительные значения 1, 2, … и определяющее принадлежность электрона к той или иной орбите; h – постоянная Планка. Все другие орбиты «запрещены». Таким образом Бор постулировал, что энергия электрона в атоме может принимать строго определенные дискретные значения ,…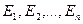

2. Двигаясь по стационарным орбитам, электрон не излучает и не поглощает электромагнитных волн.

3. Излучение происходит лишь при переходе электрона из ста­ционарного состояния с большим значением энергии 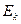в другое стационарное состояние с меньшим значением энергии 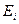. При этом излучается квант энергии (фотон) строго определенной частоты. Излучение атома монохроматично, и частота его определяется фун­даментальным соотношением (условие частот Бора)

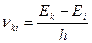, (5)

где 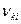- энергия излученного фотона.

Из соотношения (5) следует, что излучение происходит при пере­ходе электрона с внешних орбит на внутренние. Если же электрон переходит с внутренних орбит на внешние, то энергия поглощается.

Вычислим радиусы стационарных орбит и полную энергию электрона в водородоподобном атоме. С учетом (1) и условия квантования Бора (4) имеем для значений радиусов стационарных орбит и энергий стационарных состояний соответственно

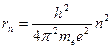; (6)

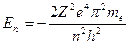. (7)

Из формулы (7) следует, что квантовое число n определяет энергию электрона в атоме, так как остальные величины остаются постоянными.

В общем случае атомная система, состоящая из ядра и одного электрона, переходя из стационарного состояния, характеризуе­мого главным квантовым числом 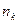, в состояние с главным кванто­вым числом 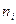, испускает по условию частот Бора спектральные линии с частотами

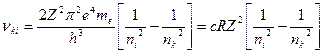, (8)

где постоянная величина

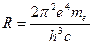(9)

называется постоянной Ридберга.

Так как по определению, в терминах волновых чисел 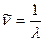, имеем

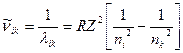. (10)

Этот закон – один из самых точных в физике. Из него прежде всего и следует, что все линии спектра могут быть объединены в се­рии. Серией называется совокупность спектральных линий, описы­ваемых формулой (10) при 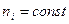, т. е. серия возникает при пе­реходе электрона с вышележащих орбит на орбиту с заданным кван­товым числом .

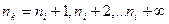Формулу (10) можно представить в виде

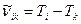, (11)

где 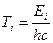, 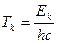- сериальные термы, пропорциональные значениям энергии атома с точностью до некоторой аддитивной постоянной. В связи с этим приобретает физический смысл и постоянная Ридберга R – это число, пропорциональное энергии атома в основном состоянии.

В спектр испускания водорода входит несколько серий, расположенных в различных областях спектра:

а) серия Лаймана – крайняя ультрафиолетовая область

,

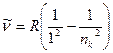где , ;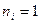

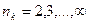б) серия Бальмера – видимая и близкая ультрафиолетовая области

,

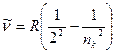где , ;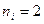

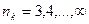в) серия Пашена – инфракрасная область спектра

,

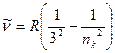где , ;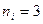

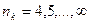г) серия Брэккета – инфракрасная область спектра

,

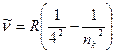где , ;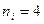

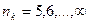д) серия Пфунда – инфракрасная область спектра

,

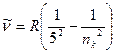где , .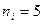

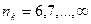Схема энергетических уровней атома водорода и соответствующих переходов показана на рис. 1. Как видно из рисунка, головными линиями каждой серии являются линии, частоты которых могут быть рассчитаны по формуле

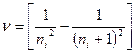. (12)

Заштрихованные переходы соответствуют границе серии и определяются формулой (8), если в ней 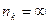, т.е. их частота выразится в виде

.

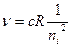Особый интерес представляет определение граничной серии Лаймана 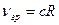, что следует из сериальной формулы при 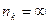. Зная частоту граничной линии Лаймана, можно определить энер­гию, необходимую для отрыва электрона от атома водорода, нахо­дящегося в нормальном, или в основном, состоянии с 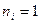. Эта энергия называется энергией ионизации и вычисляется по формуле

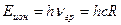. (13)

Для водородоподобного атома

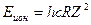. (14)

Таким образом, зная значения констант h, с, R и е, можно вычислить энергию ионизации водородоподобного атома по формуле (14).

Следует подчеркнуть, что имеются различия между экспериментально найденным значение постоянной Ридберга и теоретическим значением, что видно из следующих данных : R_т = 109737,303 см^-1; R = 109677,581 см^-1. Расхождение объясняется тем, что при выводе формулы (13) ядро водородоподобного атома считалось неподвижным, то есть имеющим бесконечно большую массу. В действительности же ядро имеет конечную массу. С учетом этого в результате взаимодействия движущегося электрона с ядром (протоном) происходит движение обеих частиц вокруг общего центра инерции атома. В формулу для постоянной Ридберга вместо массы электрона т_е войдет приведенная масса 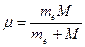, где M - масса ядра. Следовательно, энергия стационарного состояния и по­стоянная Ридберга должны зависеть от массы ядра

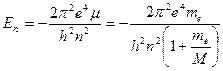, (15)

то есть

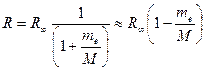, (16)

где 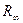- постоянная Ридберга, вычисленная в предположении бесконечно тяжелого ядра.