Общие сведения. Известно, что движение заряженной частицы в пространстве в присутствии электрического и магнитного полей определяется силой Лорентца:
Известно, что движение заряженной частицы в пространстве в присутствии электрического и магнитного полей определяется силой Лорентца:
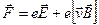 , (1)
, (1)
где 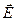 - напряженность электрического поля;
- напряженность электрического поля; 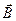 - индукция магнитного поля;
- индукция магнитного поля;  и e – скорость и заряд частицы соответственно.
и e – скорость и заряд частицы соответственно.
Анализ выражения (1) показывает, что при произвольной ориентации векторов 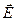 ,
, 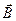 и
и  первый член в правой части (1) будет определять величину проекции вектор скорости
первый член в правой части (1) будет определять величину проекции вектор скорости  на направление вектора напряженности электрического поля
на направление вектора напряженности электрического поля 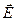 , а второй член в правой части (1) – величину проекции вектора скорости
, а второй член в правой части (1) – величину проекции вектора скорости  на направление, ортогональное вектору индукции магнитного поля
на направление, ортогональное вектору индукции магнитного поля 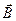 . Траектория движения частицы при этом будет иметь вид некоторой винтовой линии.
. Траектория движения частицы при этом будет иметь вид некоторой винтовой линии.
В данной работе предлагается использовать особенности движения заряженных частиц в присутствии полей для определения удельного заряда электрона 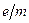 .
.
Рассмотрим частный случай для параксиального пучка электронов, когда векторы напряженности электрического поля и индукции магнитного поля коллинеарны, причем оба поля однородны. Допустим, что электрон имеет направление вектора скорости, составляющее угол α с направлением векторов 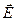 и
и 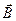 . В силу параксиальности пучка будем считать, что угол α мал. Скорость электрона можно разложить на две составляющие: тангенциальную
. В силу параксиальности пучка будем считать, что угол α мал. Скорость электрона можно разложить на две составляющие: тангенциальную  , направленную вдоль направления полей, и нормальную, перпендикулярную направлению полей (рис. 1). При этом тангенциальная составляющая скорости определяется формулой
, направленную вдоль направления полей, и нормальную, перпендикулярную направлению полей (рис. 1). При этом тангенциальная составляющая скорости определяется формулой
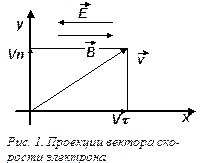
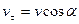 ,
,
а нормальная составляющая – формулой
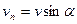 .
.
Как следует из вышесказанного, в данной комбинации полей величина тангенциальной составляющей скорости электрона будет определяться электрическим полем, а величина нормальной составляющей – магнитным.
Поскольку угол между векторами  и
и 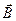 равен
равен 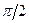 , векторное произведение, представляющее второй член правой части (1) сведется к выражению
, векторное произведение, представляющее второй член правой части (1) сведется к выражению
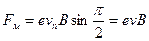 . (2)
. (2)
Так как магнитная составляющая силы Лорентца  выражается векторным произведением, то вектора
выражается векторным произведением, то вектора 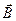 ,
,  ,
,  ортогональны и электрон под действием силы
ортогональны и электрон под действием силы  будет двигаться по окружности, радиус которой можно определить, если учесть, что сила
будет двигаться по окружности, радиус которой можно определить, если учесть, что сила  является центростремительной силой:
является центростремительной силой:
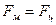 ;
; 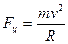 ;
; 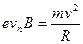 ,
,
откуда
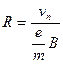 ;
; 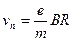 . (3)
. (3)
Период обращения электрона по этой окружности можно определить из выражения
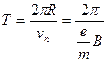 , (4)
, (4)
которое показывает, что период не зависит от радиуса R. Наличие электрической составляющей силы Лоренца приведет к тому, что в направлении векторов 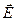 и
и 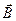 движение электрона будет равноускоренным (или равнозамедленным в зависимости от направления вектора
движение электрона будет равноускоренным (или равнозамедленным в зависимости от направления вектора 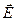 ) и в целом траектория электрона будет представлять винтовую линию с переменным шагом (рис. 2, а). В том случае, если движение электрона происходит в неоднородном магнитном поле, будет изменяться и радиус кривизны траектории (рис. 2, б). В отсутствие электрического поля шаг винтовой линии, описывающей траекторию электрона будет постоянным (рис. 2, в). Величина шага, определяемая выражением
) и в целом траектория электрона будет представлять винтовую линию с переменным шагом (рис. 2, а). В том случае, если движение электрона происходит в неоднородном магнитном поле, будет изменяться и радиус кривизны траектории (рис. 2, б). В отсутствие электрического поля шаг винтовой линии, описывающей траекторию электрона будет постоянным (рис. 2, в). Величина шага, определяемая выражением
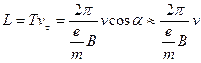 , (5)
, (5)
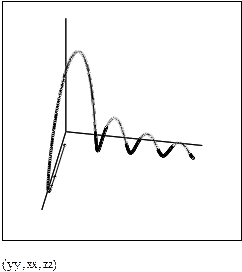


Рис. 2. Траектория электрона в параллельных электрическом и магнитном полях. Поля направлены вдоль оси oZ. Верхний левый график - неоднородное магнитное поле, однородное электрическое поле; верхний правый график - однородное магнитное поле, неоднородное электрическое поле; нижний график - однородное магнитное поле, электрическое поле отсутствует, из которого видно, что для параксиального пучка шаг винтовой линии не зависит от угла между векторами скорости и индукции магнитного поля, то есть электроны, вышедшие из одной точки (предположим, что эта точка расположена на оси oZ) после одного оборота вновь сфокусируются в точке на этой же оси на расстоянии L. Если каким-либо независимым методом определить скорость электронов, то выражение (2) можно использовать для определения удельного заряда электрона 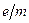 .
.
Дата добавления: 2015-02-25; просмотров: 713;
