Общие сведения. Фотоэлектрическим эффектом называется возникновение или изменение электрического тока в цепи под действием свет

Фотоэлектрическим эффектом называется возникновение или изменение электрического тока в цепи под действием свет, падающего на один элемент этой цепи. В настоящее время различают три рода фотоэффекта:

· внешний фотоэффект - фотоэлектронная эмиссия с поверхности тел, помещенных в вакуум или газ и освещаемых светом;

· фотопроводимость кристаллов - появление под действием света добавочных электронов проводимости внутри полупроводника, что ведет к уменьшению сопротивления облучаемого светом тела;

· фотоэффект запирающего слоя - возникновение под действием света, падающего на границу металл-полупроводник, электродвижущей силы, вызывающей появление или изменение тока в цепи.

В настоящей лабораторной работе предлагается изучить некоторые закономерности внешнего фотоэффекта, которые имеют особое значение для понимания квантовых представлений о природе света.

Внешний фотоэффект на поверхности металла был впервые обнаружен в 1887 году Герцем при изучении условий возникновения искрового разряда в резонаторах, при помощи которых он исследовал распространение открытых им электромагнитных волн.

В 1888 - 1890 годах профессор Московского университета А.Г.Столетов провел обширное исследование фотоэлектронной эмиссии.

Многочисленные исследования испускания электронов поверх­ностью металла (фотокатодом) под действием падающего на нее потока световой энергии привели к выводу следующих основных законов внешнего фотоэффекта.

1. Сила фотоэлектрического тока насыщения, а следовательно, и количество фотоэлектронов, вылетающих в единицу времени с единицы поверхности фотокатода, при освещении монохроматиче­ским светом пропорционально величине интенсивности падающего излучения, если при изменении интенсивности спектральный состав излучения остается неизменным (закон Столетова), т. е.

, (1)

где k — коэффициент пропорциональности, характеризующий чувст­вительность данной поверхности к свету.

2. Максимальная энергия фотоэлектронов и их скорость не за­висят от интенсивности падающего на фотокатод излучения и явля­ются функцией частоты падающего монохроматического света: они линейно растут с увеличением частоты падающего излучения (закон Эйнштейна).

3. Число фотоэлектронов, вылетающих в единицу времени с единицы поверхности, при постоянной интенсивности излучения увеличивается с ростом частоты падающего излучения.

Перечисленные законы внешнего фотоэффекта не объясняются классической электродинамикой. Фотоэффект принадлежит к числу явлений, в которых обнаруживаются корпускулярные свойства света. Поэтому теоретическое объяснение количественных закономерностей фотоэффекта в современной физике можно дать только на основе квантовых представлений о свете, т. е. сущность фотоэффекта вскрывается квантовой теорией излучения.

Согласно квантовой теории света, все тела излучают или поглощают световую энергию не непрерывно, а отдельными порциями – квантами света (фотонами). Интерференция и дифракция свидетельствуют о том, что световые излучения обладают и волновыми свойствами. Поэтому каждому кванту энергии может быть приписана определенная частота. Энергия одного кванта пропорциональна частоте колебаний и равна

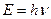(2)

где h - постоянная Планка; n - частота падающего монохроматического света. Энергия светового кванта, упавшего на поверхность вещества, в результате столкновения с электронами поглощается и приводит к «выбиванию» электронов из фотокатода.

Основное уравнение фотоэффекта представляет собой закон сохранения энергии и устанавливает связь межу энергией кванта, вызывающего фотоэффект, работой выхода электронов из металла энергией вылетающего электрона. Уравнение имеет вид

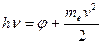, (3)

где m_e – масса электрона; v – максимальная скорость электрона при выходе из поверхности металла; j – эффективная работа выхода. Это выражение называется уравнением Эйнштейна. Следует обратить внимание на то, что даже при монохроматическом освещении энергия фотоэлектронов, вылетающих из фотокатода, оказывается неодинаковой. Фотоэлектроны проходят внутри фотокатода некоторый и притом различный для разных электронов слой вещества и замедляют свое движение, поэтому их энергия уменьшается. Соотношение (3) определяет поэтому кинетическую энергию не всех, а только наиболее быстрых фотоэлектронов.

Закон Эйнштейна непосредственно приводит к представлению о красной границе (пороге) фотоэффекта. Из уравнения (3) следует, что если работа выхода f фотоэлектрона меньше энергии фотона, то величина

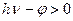и 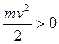, т.е. v > 0.

Для каждого металла должна существовать некоторая минимальная частота света, при которой еще возможен вылет электронов. Эта минимальная частота n₀ определяется из равенства

и . (4)

Для частоты 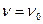энергия фотона такова, что может быть совершена только работа выхода и вылетевший электрон покидает поверхность катода со скоростью, равной нулю.

Для кванта энергии с частотой , т. е. при 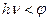, электроны проводимости не могут выйти из катода за счет энергии поглощенного кванта, так как энергия эта недостаточна для преодоления работы выхода, и фотоэффект не наблюдается. Частота, определяемая из выражений (4), дает ту минимальную частоту, при которой возможен фотоэффект, т. е. определяет порог фотоэффекта и называется предельной или граничной частотой фотоэффекта. Длина волны 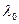, соответствующая предельной частоте 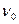и определяемая по формуле

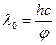, (5)

называется красной границей фотоэффекта. Величина 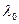зависит от природы вещества, состояния поверхности катода и особенно от наличия пленок адсорбированного газа. Для большинства веществ 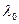лежит в ультрафиолетовой области спектра. Однако у некоторых металлов с малой работой выхода (особенно у щелочных – Na, К, Rb, Cs) наблюдается фотоэффект при видимом свете и красная граница лежит в видимой и инфракрасной областях спектра.

Электроны, вылетевшие из катода фотоэлемента под действием света, обладают определенной кинетической энергией и, достигая анода, создают в замкнутой цепи, доставленной из фотоэлемента и гальванометра, ток. Если между анодом и катодом создать электрическое поле, приложив разность потенциалов, то можно затормозить электроны. Методом задерживающего потенциала обычно пользуются при измерении энергии фотоэлектронов. Те электроны, кинетическая энергия которых удовлетворяет условию , не могут достичь анода. Поэтому при увеличении U анодный ток падает, и при некотором значении разности потенциалов U = U_з (потенциал запирания) даже самые наиболее быстрые фотоэлектроны не могут достичь анода, и анодный ток в цепи прекращается.

Максимальная кинетическая энергия фотоэлектронов связана с задерживающим потенциалом U_з соотношением

. (6)

Экспериментально изучается зависимость электронного тока в фотоэлементе от величины приложенного задерживающего потенциала U_з. Эта зависимость выражается плавной кривой. Практический интерес представляет точка пересечения кривой с осью U = 0, определяющая потенциал запирания (рис. 1). Подстановка (6) в (3) дает

,

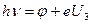или

.

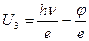Это есть уравнение прямой линии, откуда видно, что задерживаю­щий потенциал U_з зависит от частоты света, падающего на фото­элемент. При экспериментальной проверке уравнения Эйнштейна можно убедиться в том, что величина задерживающего потенциала зависит только от частоты света n, причем линейно (рис. 2).

Если исследовать зависимость задержи­вающего потенциала от частоты света, то можно определить постоянную Планка и работу выхода электронов по формулам ; (7)

(8)

где и задерживающие потенциалы для частот n₁ и n₂. Точка пересечения прямой с осью абсцисс дает численное значение граничной частоты n₀.