Расчет опор воздушных линий электропередачи
4.1 Расчет деревянной П - образной опоры
На П-образную промежуточную опору линии электропередачи, представленную на рисунке 4.1, действует ветер со скоростью «v», направленный параллельно проводам. Кроме того, в результате обрыва одного или нескольких проводов на траверсу действуют силы натяжение проводов Т. Вертикальными силами пренебречь.
Требуется определить:
1) построить эпюры поперечных сил и изгибающих моментов для траверсы и наиболее загруженной стойки;
2) определить максимальные нормальные напряжения в опасных сечениях стойки и траверсы;
3) проверить прочность стойки и траверсы, если допускаемые нормальные напряжения материала опоры [σ] = 12 МПа.
Примечание: траверсу и стойку считать цилиндрическими с диаметром траверсы 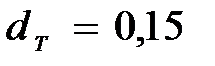 м и диаметрами стоек
м и диаметрами стоек 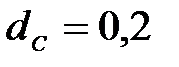 м.
м.
Погонные нагрузки от ветра на траверсу и стойки определить по зависимостям:
- нагрузку на траверсу 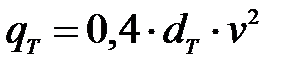 (Н/м);
(Н/м);
- нагрузку на стойки 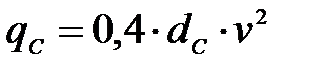 (Н/м).
(Н/м).
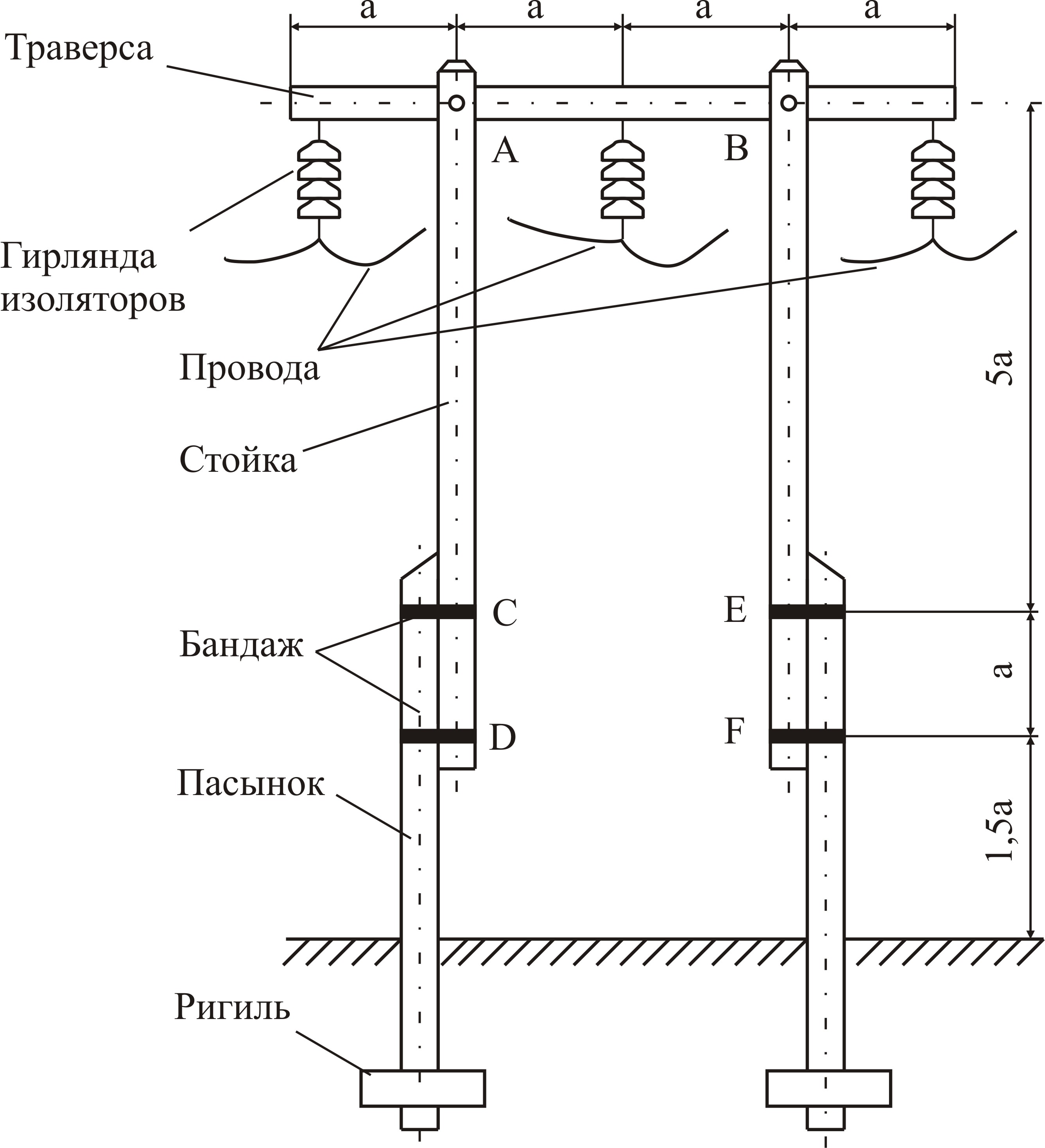
Рисунок 4.1 – Промежуточная П-образная опора
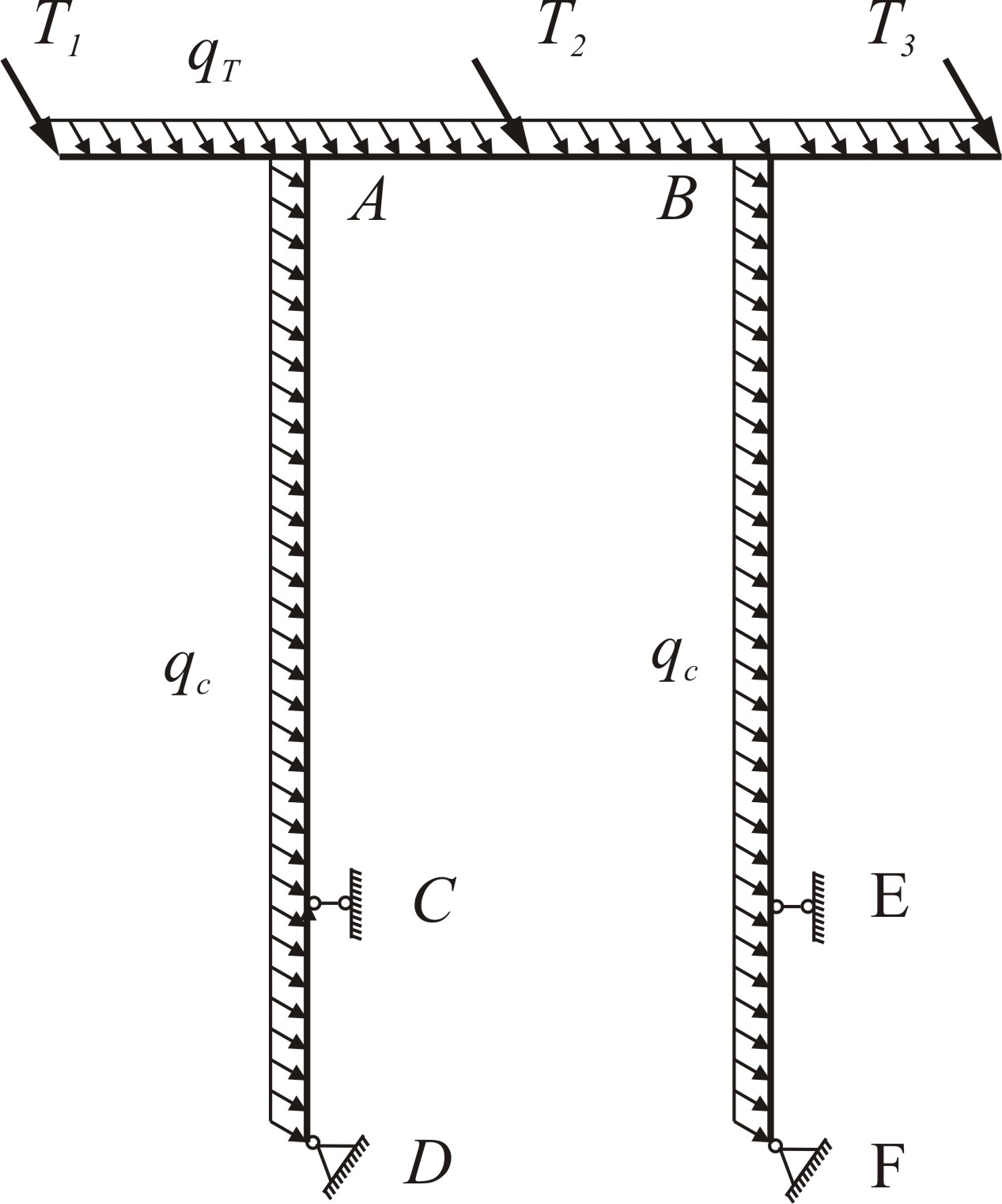
Рисунок 4.2 – Схема загружения опор и траверсы
Материалом, из которой выполнена опора, является дерево.
Деревянные опоры получили наибольшее распространение при строительстве ВЛ, что обусловлено их невысокой стоимостью, достаточно высокой механической прочностью, а также природным круглым сортаментом, обеспечивающим простоту конструкций и наименьшее сопротивление ветровым нагрузкам. Для изготовления деревянных опор применяют сосну, лиственницу и реже ель. Деревянные промежуточные опоры могут быть гибкими, к ним относятся одностоечные и простые П-образные конструкции, или жесткими, имеющими большую жесткость поперек линии, к ним относятся П-образные конструкции с ветровыми связями – раскосами и конструкции анкерных угловых опор.
Траверса и стойки П-образной опоры от ветровой нагрузки (без учета собственного веса) испытывают деформацию плоского или прямого изгиба, при котором в поперечных сечениях стержней под воздействием внешних сил возникают внутренние поперечная сила 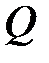 и изгибающий момент
и изгибающий момент 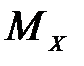 .
.
Для определения положения опасного сечения и численного значения внутренних усилий в нем строят с помощью метода сечений эпюры.
Поперечная сила Q в сечении равна алгебраической сумме проекций всех внешних сил, расположенных по одну сторону сечения, на ось, перпендикулярную геометрической оси балки [9].
Изгибающий момент МX в произвольно выбранном поперечном сечении балки равен алгебраической сумме моментов всех внешних нагрузок, действующих по одну сторону этого сечения относительно поперечной оси сечения.
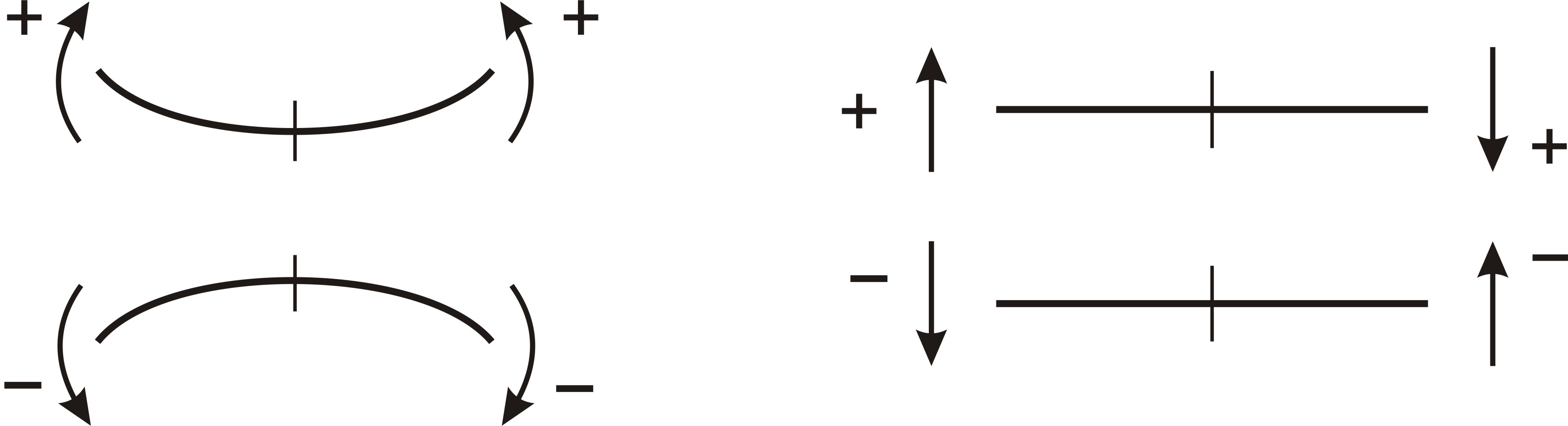
Рисунок 4.3 Рисунок 4.4
В соответствии с рисунком 4.3 при составлении выражения изгибающего момента принято считать моменты внешних сил положительными, если они стремятся сжать верхнее волокно балки и растянуть нижнее, и считаются отрицательными, если стремятся растянуть верхнее волокно и сжать нижнее.
В соответствии с рисунком 4.4, при составлении выражения для поперечной силы, принято считать внешние силы положительными, если они стремятся повернуть оставшуюся часть относительно сечения по ходу часовой стрелки, и, наоборот.
Между интенсивностью распределенной нагрузки 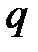 , поперечной силой
, поперечной силой 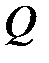 и изгибающим моментом
и изгибающим моментом 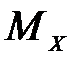 существует дифференциальная зависимость
существует дифференциальная зависимость
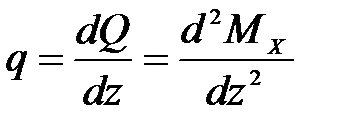 . (4.1)
. (4.1)
Эпюры 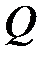 и
и 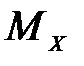 можно строить, предварительно составляя уравнение, выражающие изменения
можно строить, предварительно составляя уравнение, выражающие изменения 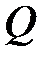 и
и 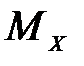 по участкам или без уравнений по характерным точкам, используя следствия из дифференциальных зависимостей между
по участкам или без уравнений по характерным точкам, используя следствия из дифференциальных зависимостей между 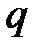 ,
, 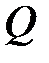 и
и 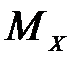 формулы (4.1), а также некоторые положения метода сечения.
формулы (4.1), а также некоторые положения метода сечения.
Основные правила построения эпюр
а) На участке, свободном от распределенной нагрузки ( 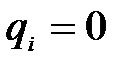 ):
):
1) эпюра 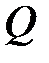 ограничивается прямой параллельной оси линией;
ограничивается прямой параллельной оси линией;
2) эпюра 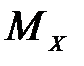 ограничивается прямой наклонной линией.
ограничивается прямой наклонной линией.
б) На участке с распределенной нагрузкой ( 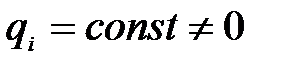 ):
):
1) эпюра 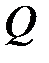 ограничена прямой наклонной линией, наклоном в направлении нагрузки при обходе эпюры слева направо (и наоборот – в противоположном направлении
ограничена прямой наклонной линией, наклоном в направлении нагрузки при обходе эпюры слева направо (и наоборот – в противоположном направлении 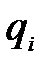 при обходе справа налево), а общее изменение
при обходе справа налево), а общее изменение 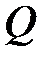 (разница ординат) равно равнодействующей нагрузки на данном участке;
(разница ординат) равно равнодействующей нагрузки на данном участке;
2) эпюра 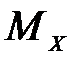 ограничена параболой, выпуклость которой обращена навстречу распределенной нагрузке.
ограничена параболой, выпуклость которой обращена навстречу распределенной нагрузке.
в) В сечениях, где к балке приложена сосредоточенная сила:
1) на эпюре 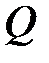 скачок (разрыв линий, ограничивающих эпюру на соседних участках) в направлении действия этой силы (если эпюру обходить слева направо) и на величину этой силы;
скачок (разрыв линий, ограничивающих эпюру на соседних участках) в направлении действия этой силы (если эпюру обходить слева направо) и на величину этой силы;
2) на эпюре 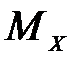 - перелом, направленный острием навстречу силе.
- перелом, направленный острием навстречу силе.
г) В сечении, где к балке приложен внешний сосредоточенный момент (пара сил):
1) на эпюре 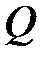 - никаких изменений;
- никаких изменений;
2) на эпюре 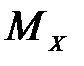 - скачок на величину этого момента – в плюс (+), если момент положительный; в минус – если отрицательный.
- скачок на величину этого момента – в плюс (+), если момент положительный; в минус – если отрицательный.
д) В сечении, где 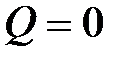 на участке с распределенной нагрузкой, на эпюре М касательная к параболе – горизонтальная, т.е. М имеет относительный экстремум (экстремум положительный, если
на участке с распределенной нагрузкой, на эпюре М касательная к параболе – горизонтальная, т.е. М имеет относительный экстремум (экстремум положительный, если 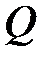 меняет знак с «плюса» на «минус» слева направо, и наоборот).
меняет знак с «плюса» на «минус» слева направо, и наоборот).
е) В сечении, где 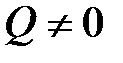 и меняет знак, изгибающий момент экстремален.
и меняет знак, изгибающий момент экстремален.
ж) В крайней шарнирной опоре или на свободном конце консоли, если не приложен внешний сосредоточенный момент, на эпюре изгибающего момента М=0.
Расчет на прочность при плоском поперечном изгибе производят по нормальным напряжениям, так как нормальные напряжения, вызванные изгибающим моментом 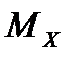 , значительно превосходят касательные напряжения, вызванные поперечной силой
, значительно превосходят касательные напряжения, вызванные поперечной силой 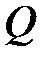 .
.
Условие прочности по нормальным напряжениям для сечения симметричного относительно нейтральной оси имеет вид
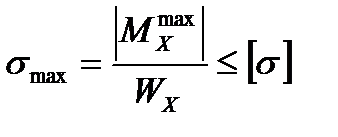 (4.2)
(4.2)
где 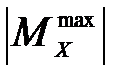 - изгибающий момент в опасном сечении балки;
- изгибающий момент в опасном сечении балки;
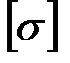 - допускаемое нормальное напряжение материала балки;
- допускаемое нормальное напряжение материала балки;
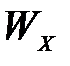 - осевой момент сопротивления поперечного сечения балки.
- осевой момент сопротивления поперечного сечения балки.
Для круглого поперечного сечения
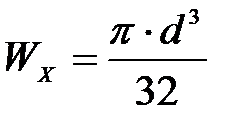 (4.3)
(4.3)
где 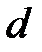 - диаметр поперечного сечения.
- диаметр поперечного сечения.
При проверочном расчете необходимо выяснить соблюдение или несоблюдение условия прочности.
Пример расчета П-образной опоры
На П-образную промежуточную опору линии электропередачи, изображенную на рисунке 4.1, действуют со скоростью 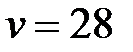 м/с ветер, направленный параллельно проводам. Кроме того, в результате обрыва на траверсу действуют натяжения проводов
м/с ветер, направленный параллельно проводам. Кроме того, в результате обрыва на траверсу действуют натяжения проводов 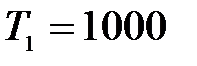 H,
H, 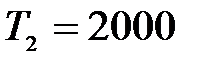 H и
H и 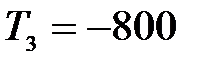 H. Требуется:
H. Требуется:
1) построить эпюры поперечных сил и изгибающих моментов для траверсы и наиболее загруженной стойки;
2) проверить прочность стойки и траверсы, если допускаемое нормальное напряжение материала опоры 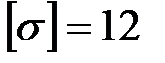 МПа.
МПа.
Решение. В конструкциях на шарнирных опорах при решении любой задачи механики предварительно необходимо определить реакции опор.
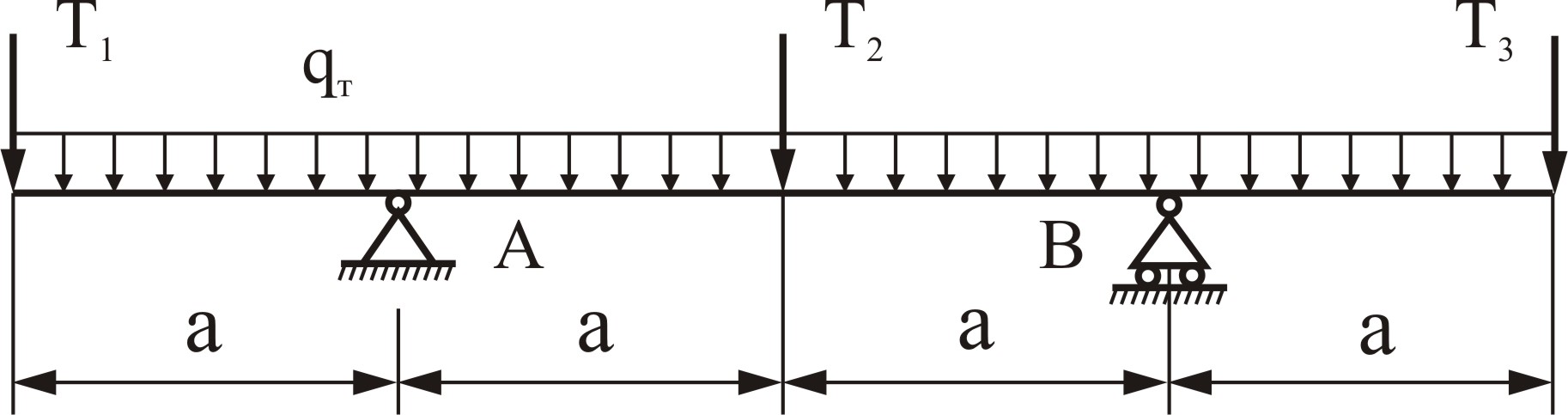
Рисунок 4.5 – Общая расчетная схема траверсы
При составлении индивидуальной расчетной схемы траверсы, представленной на рисунке 4.6, направление силы Т3 меняем на противоположное и в дальнейшем расчете знак «минус» не учитываем.
Погонную нагрузку от ветра на траверсу определяем по выражению
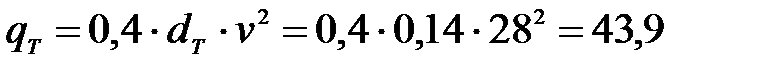 Н/м
Н/м
Погонная нагрузка от ветра на стойки определяем по выражению
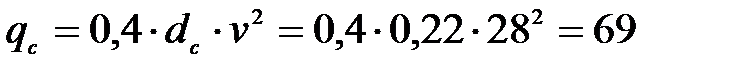 Н/м
Н/м
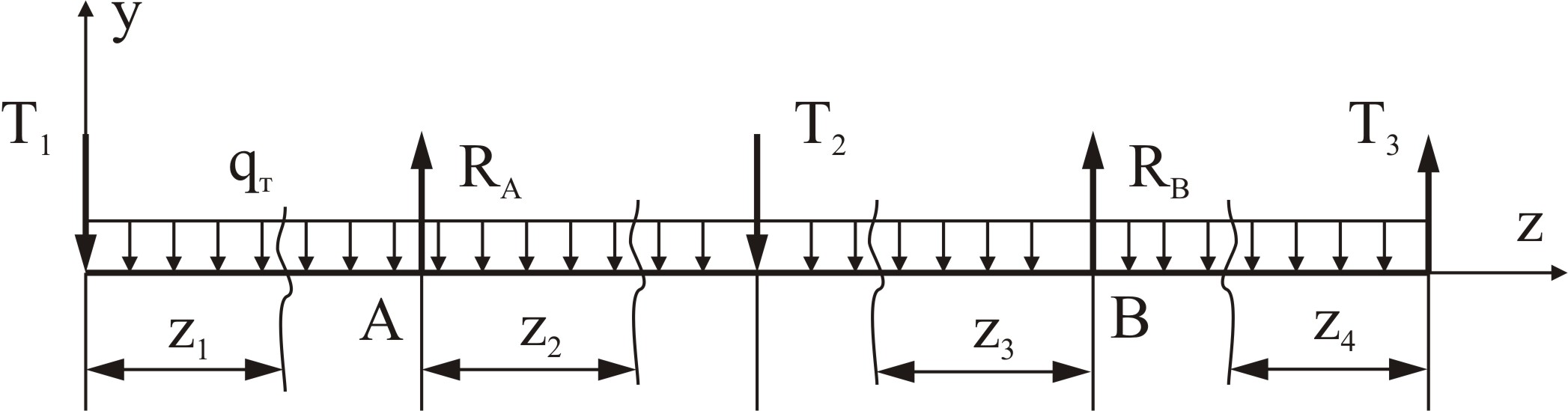
Рисунок 4.6 – Индивидуальная расчетная схема траверсы
Реакции в опорах А и В определим из условий равновесия
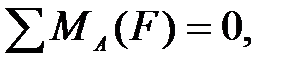
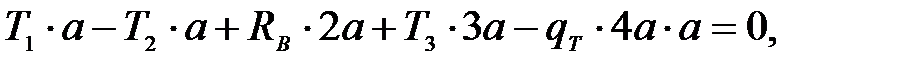
откуда 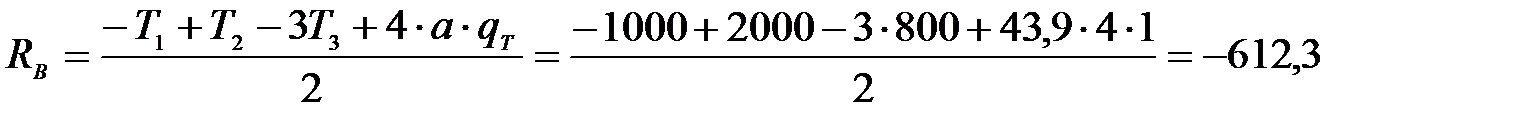 кН.
кН.
Знак «минус» указывает на то, что реакция 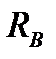 направлена вниз, то есть противоположно ранее принятому.
направлена вниз, то есть противоположно ранее принятому.
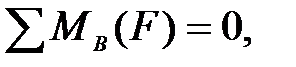
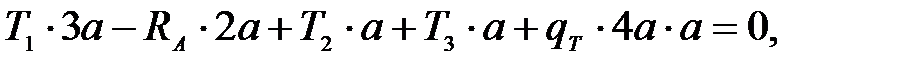
откуда 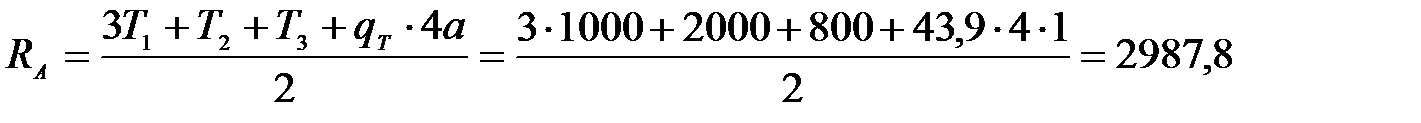 кН.
кН.
Проверим значение найденных реакций. Если равенство соблюдается, то реакции определены верно.
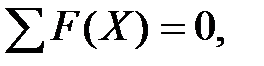
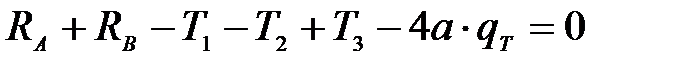 ,
,
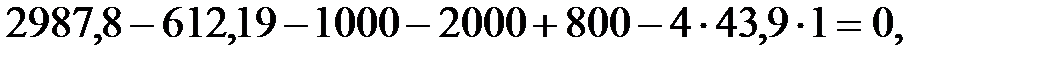
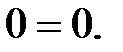
При построении эпюр внутренних усилий и изгибающих моментов пользуемся методом сечений, предварительно разбив балку на участки.
Построение эпюр внутренних усилий для траверсы
1 участок: 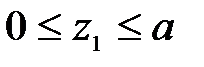
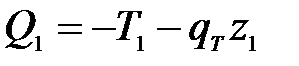 ;
;
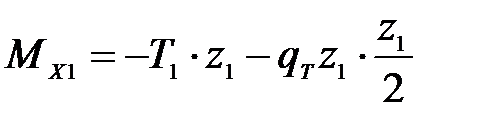 ;
;
при 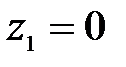 ,
, 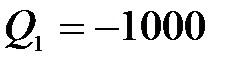 Н,
Н,
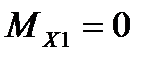 Н·м;
Н·м;
при 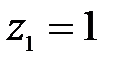 м,
м, 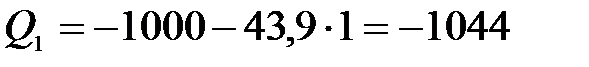 Н,
Н,
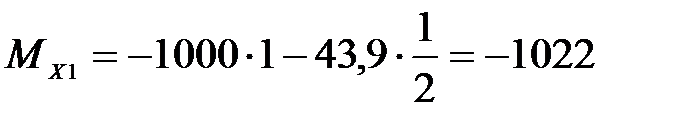 Н·м.
Н·м.
2 участок: 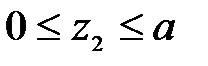
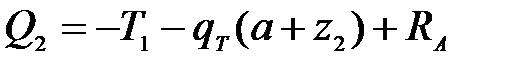 ;
;
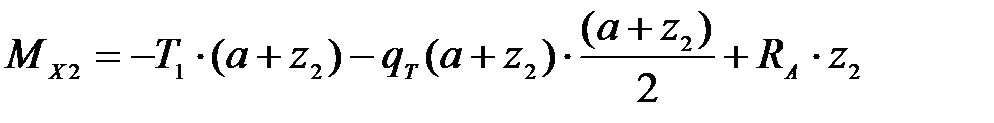 ;
;
при 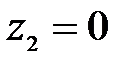 ,
, 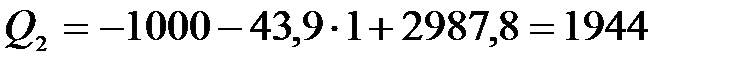 Н,
Н,
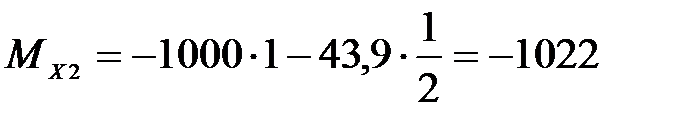 Н·м;
Н·м;
при 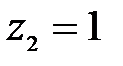 м,
м, 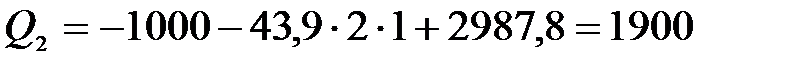 Н,
Н,
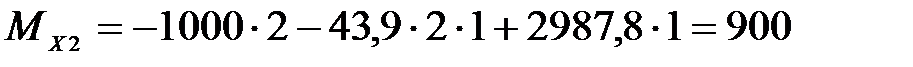 Н·м.
Н·м.
3 участок: 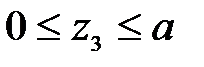
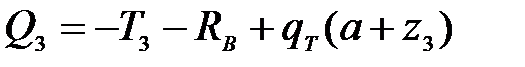 ;
;
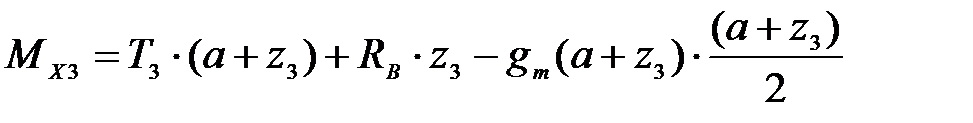 ;
;
при 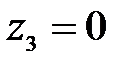 ,
, 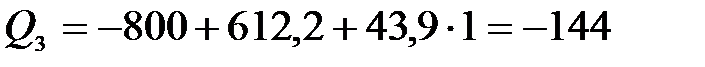 Н,
Н,
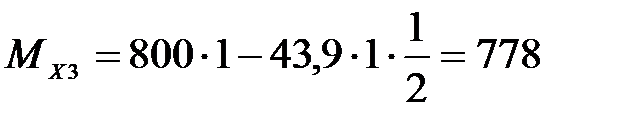 Н·м;
Н·м;
при 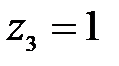 м,
м, 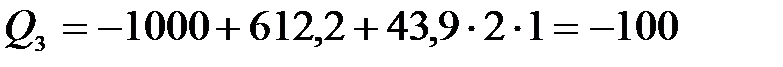 Н,
Н,
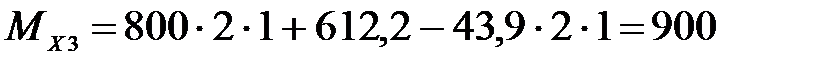 Н·м.
Н·м.
4 участок: 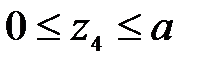
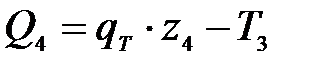 ;
;
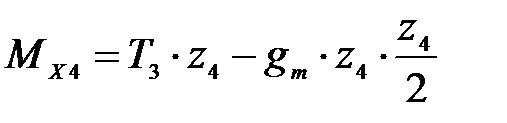 ;
;
при 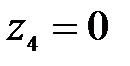 ,
, 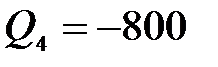 Н,
Н,
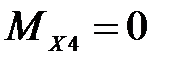 Н·м;
Н·м;
при 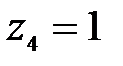 м,
м, 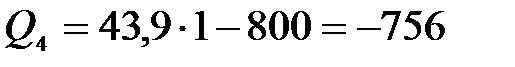 Н,
Н,
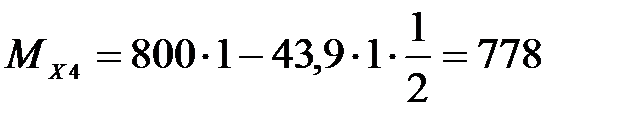 Н·м.
Н·м.
На всех четырех участках поперечная сила  меняется по линейному закону, изгибающий момент
меняется по линейному закону, изгибающий момент 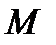 изменяется по закону квадратной параболы. Эпюры поперечных сил
изменяется по закону квадратной параболы. Эпюры поперечных сил 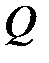 и изгибающий момент
и изгибающий момент 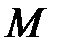 показаны на рисунке 4.7. Сведем результаты вычислений в таблицу
показаны на рисунке 4.7. Сведем результаты вычислений в таблицу
Таблица 4.1
|  ,
Н ,
Н
|  ,
Н ,
Н
| 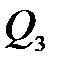 ,
Н ,
Н
| 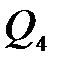 ,
Н ,
Н
| 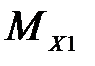 , Н*м , Н*м
| 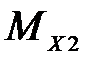 , Н*м , Н*м
| 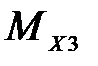 , Н*м , Н*м
| 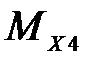 , Н*м , Н*м
|
| -1000 | -144 | -800 | -1022 | |||||
| -1044 | -100 | -756 | -1022 |
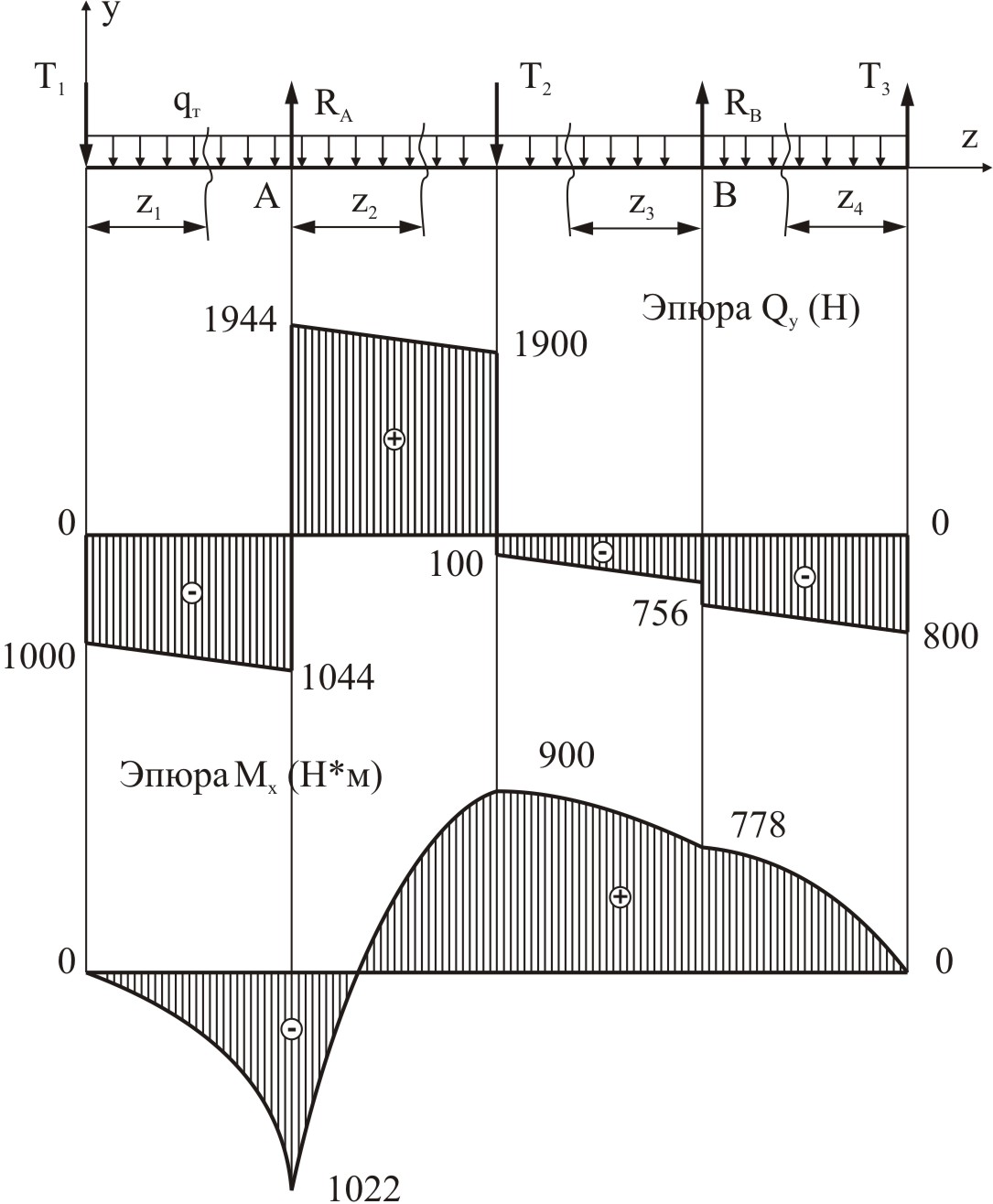
Рисунок 4.7 – Эпюра внутренних усилий траверсы
Построение эпюр внутренних усилий для наиболее загруженной стойки.
Ветровая нагрузка 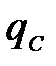 на обе стойки, представленных на рисунке 4.8, одинакова, а реакция
на обе стойки, представленных на рисунке 4.8, одинакова, а реакция 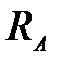 , действующая с траверсы на левую стойку, больше реакции
, действующая с траверсы на левую стойку, больше реакции 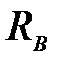 , действующей с траверсы на правую стойку.
, действующей с траверсы на правую стойку.
Кроме того, реакция 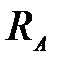 совпадает с направлением ветровой нагрузки, а
совпадает с направлением ветровой нагрузки, а 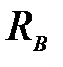 направлена противоположном направлении, поэтому более загруженной является левая стойка.
направлена противоположном направлении, поэтому более загруженной является левая стойка.
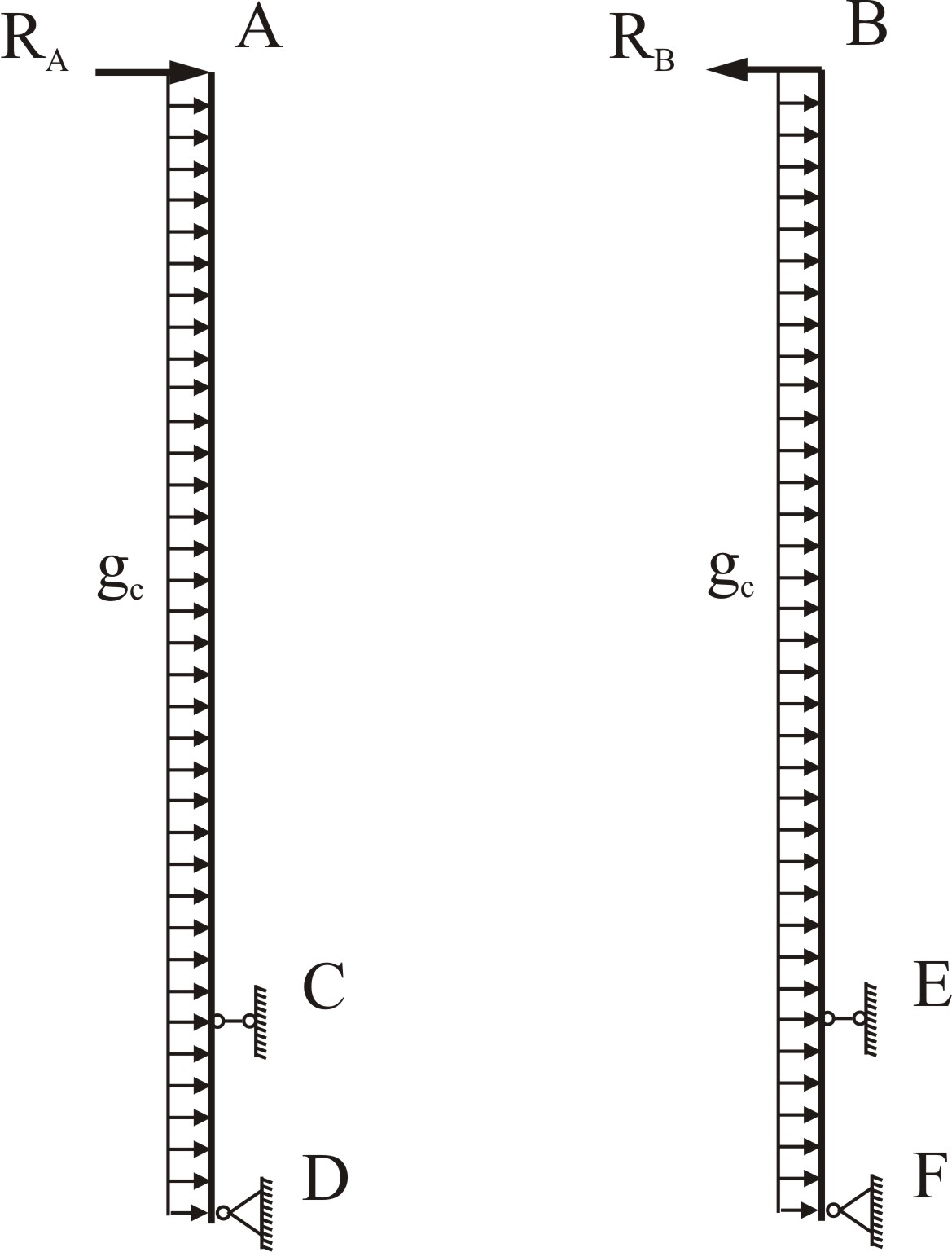
Рисунок 4.8 – Расчетные схемы левой и правой стоек
Действие связей на стойку заменяем их реакциями 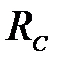 и
и 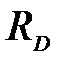 , которые определим из условий равновесия
, которые определим из условий равновесия
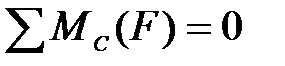 ,
, 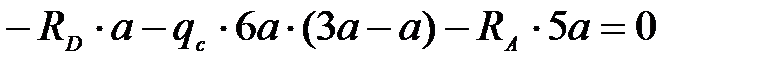 ,
,
откуда 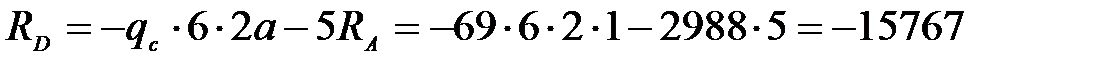 Н.
Н.
Знак «минус» указывает на то, что реакция 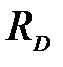 направлена в противоположном направлении ранее принятому.
направлена в противоположном направлении ранее принятому.
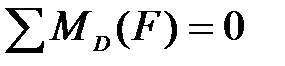 ,
, 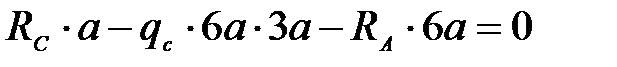 ,
,
откуда 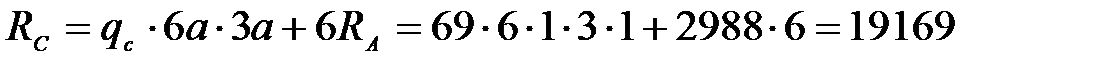 Н.
Н.
Проверим значение найденных реакций. Если равенство соблюдается, то реакции определены верно
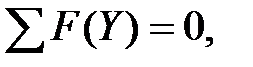
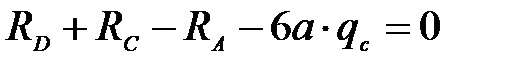 ,
,
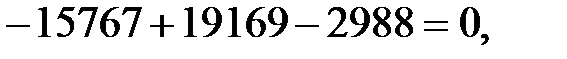
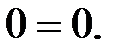
Уравнения внутренних усилий составляем для каждого из участков
Участок СD: 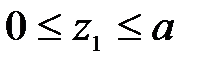
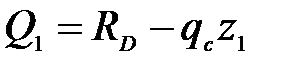 ;
;
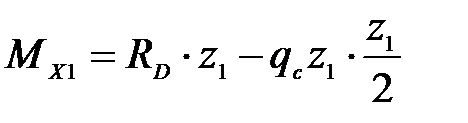 ;
;
при 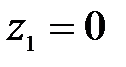 ,
, 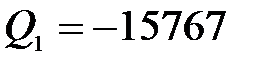 Н,
Н,
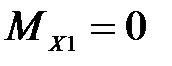 Н*м;
Н*м;
при 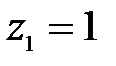 м,
м, 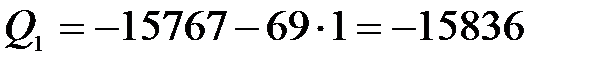 Н,
Н,
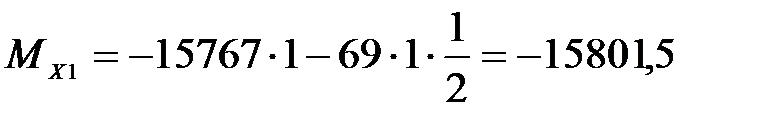 Н·м.
Н·м.
Участок СA: 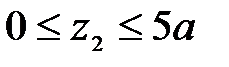
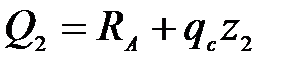 ;
;
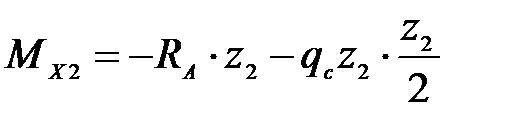 ;
;
при 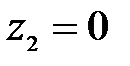 ,
, 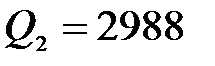 Н,
Н,
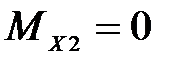 Н·м;
Н·м;
при 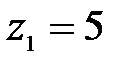 м,
м, 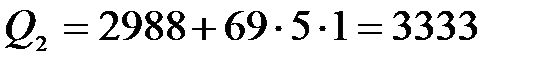 Н,
Н,
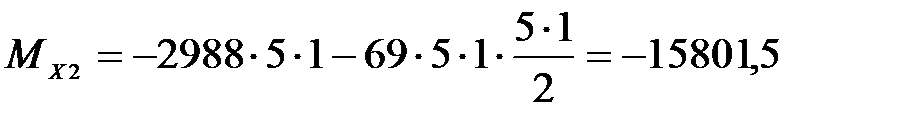 Н·м.
Н·м.
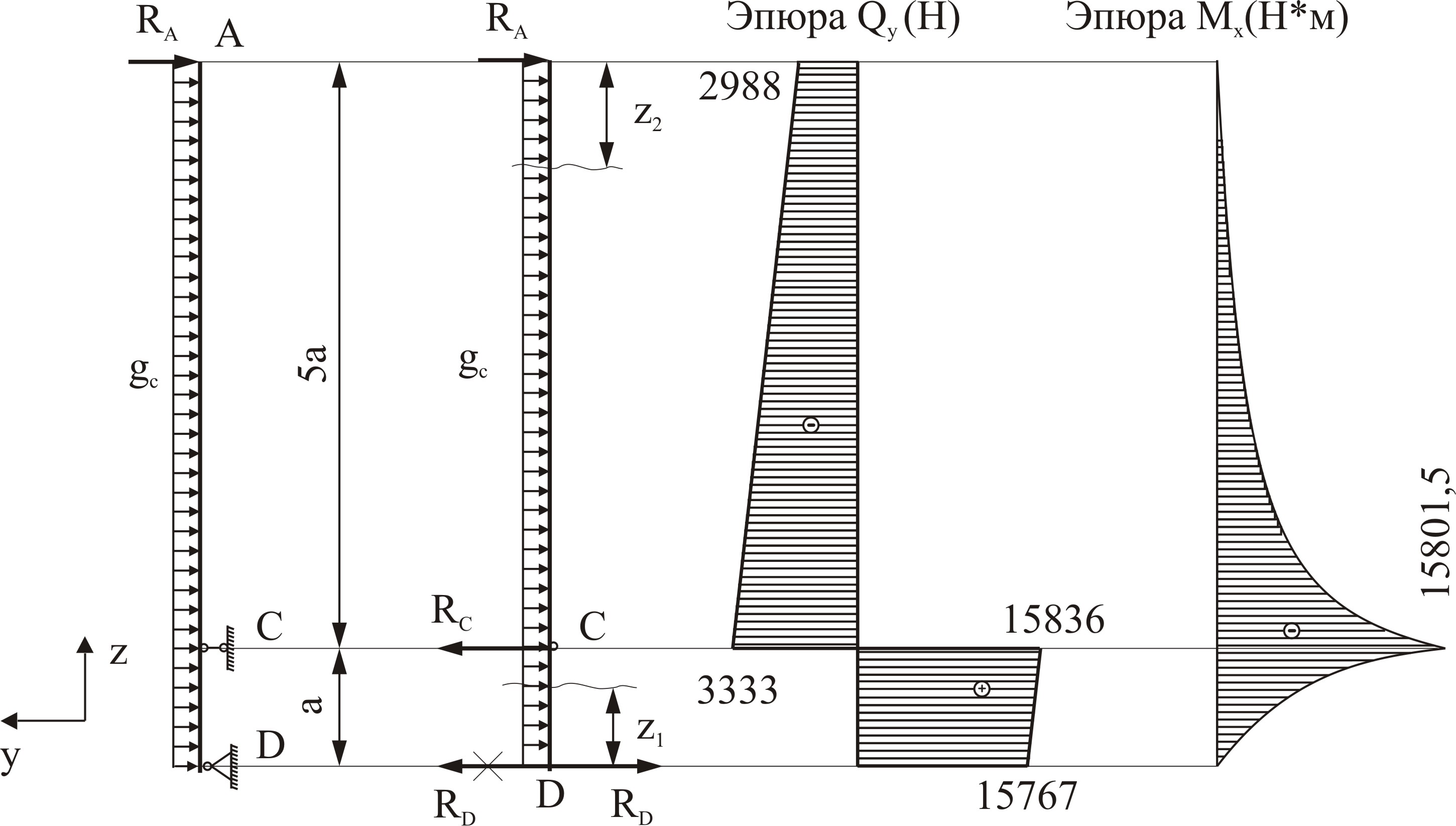
Рисунок 4.9 – Эпюры внутренних усилий левой стойки
На обоих участках поперечная сила 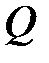 меняется по линейному закону, а изгибающий момент
меняется по линейному закону, а изгибающий момент 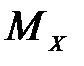 меняется по квадратной параболе.
меняется по квадратной параболе.
Для сравнения на рисунке 4.10 показаны расчетная схема, эпюры поперечных сил 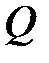 и изгибающих моментов
и изгибающих моментов 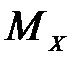 для правой стойки.
для правой стойки.
Внутренние усилия в опасном сечении правой стойки (верхний бандаж) много меньше внутренних усилий в опасном сечении левой стойки.
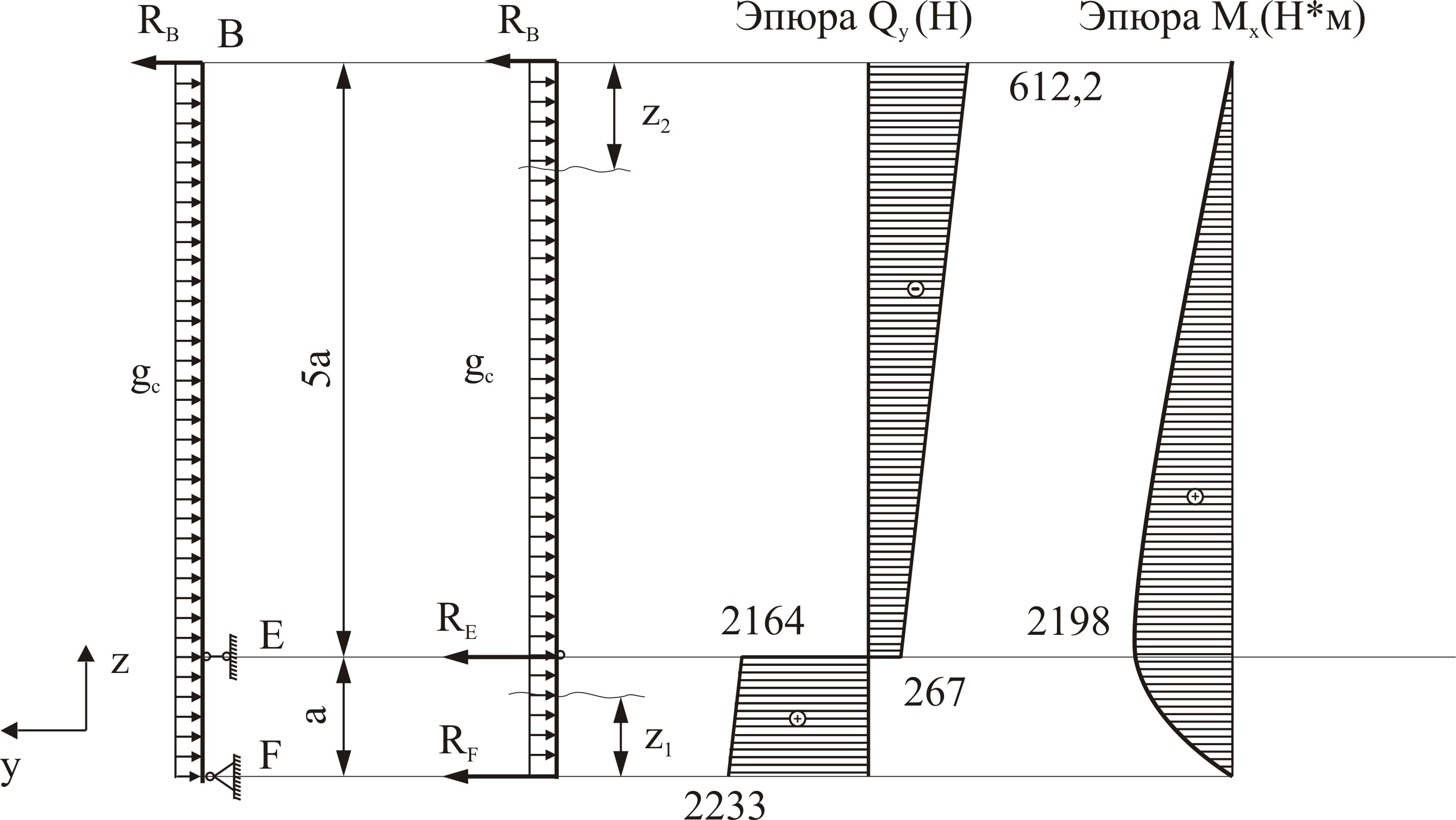
Рисунок 4.10 – Эпюры внутренних усилий правой стойки
Расчет на прочность стойки и траверсы
Если не учитывать собственный вес опоры ЛЭП, то ее элементы работают при плоском изгибе, расчет на прочность при котором производится по нормальным напряжениям. Для балки с поперечным сечением, симметричным относительно нейтральной оси, условие прочности имеет вид:
Опасным сечением траверсы является сечение А, где 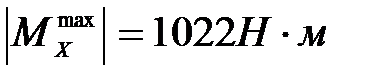 .
.
Условие прочности траверсы по формуле (4.2) с учетом формулы (4.3) примет вид:
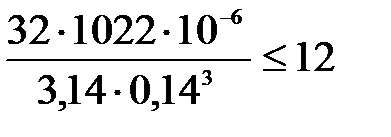 ,
,
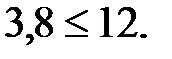
Условие прочности траверсы выполняется с запасом, траверса прочная.
Опасным сечением стойки является сечение С, где 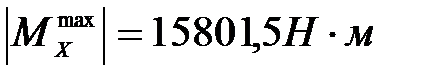 . Условие прочности стойки по формуле (4.2) с учетом формулы (4.3) примет вид
. Условие прочности стойки по формуле (4.2) с учетом формулы (4.3) примет вид
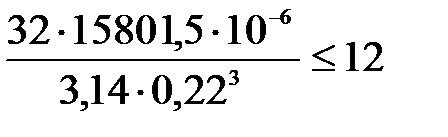 ,
,
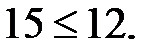
Условие прочности стойки не выполняется, левая стойка не прочная.
4.2 Расчет одностоечной опоры на прочность и устойчивость
На одностоечную деревянную опору (столб) АВ, представленную на рисунке 4.11, цилиндрической формы с диаметром «dc» и высотой «h» в точке А действует горизонтальная сила «Т» и вертикальная сила «Р» (в одной плоскости с силой «Т»), отстоящая от оси опоры на расстояние «е». Заменив схему нагружения эквивалентной расчетной схемой, изображенной на рисунке 4.12, в которой «Т», «Р» и М= Р·е приведены к точке А опоры.

Рисунок 4.11 Рисунок 4.12
Произведем расчет грузоподъемности опоры в различных случаях нагружения.
а) На столб действует горизонтальная сила Т: требуется определить:
1) из расчета на прочность определить допускаемую силу [Т], если допускаемое нормальное напряжение дерева при изгибе [σ]= 12 МПа;
2) определить максимальный прогиб столба под действием силы [Т], если модуль упругости дерева Е = 104 МПа;
б) На столб действует только осевая, центрально приложенная сила Р: требуется определить:
1) критическую силу Ркр;
2) допускаемую силу [Р] из расчета на устойчивость, если основное допускаемое напряжение дерева при сжатии [σ]сж= 12 МПа.
в) На столб действует только момент М: требуется определить из расчета на прочность допускаемое значение момента [М].
г) На столб действуют все силы – Т, Р, М. Приняв Т = 0,5 [Т], Р = 0,1 [Р], М = 0,2 [М], проверить прочность столба.
В данном случае необходимо произвести расчет грузоподъемности при различных простых видах нагружения и проверочный расчет прочности при сложном сопротивлении.
При замене Г-образной одностоечной опоры, представленную на рисунке 4.1, на эквивалентную, представленной на рисунке 4.2, мы получим стержень жестко защепленный в нижнем сечении и нагруженный в верхнем сечении горизонтальной силой Т, вертикальной силой Р и моментом пары сил 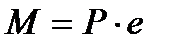 . При совместном действии этих сил стержень испытывает изгиб со сжатием, при воздействии только вертикальной силы Р – сжатие, при воздействии только горизонтальной силы Т – плоский изгиб, при воздействии одного момента М – чистый изгиб.
. При совместном действии этих сил стержень испытывает изгиб со сжатием, при воздействии только вертикальной силы Р – сжатие, при воздействии только горизонтальной силы Т – плоский изгиб, при воздействии одного момента М – чистый изгиб.
При воздействии на столб одной лишь горизонтальной силы Т, ее значение определяют из условия прочности при изгибе по формуле (4.2).
Для определения перемещений поперечных сечений при изгибе существуют различные способы, в том числе метод Мора [9]. Метод Мора представляет собой универсальный способ определения линейных и угловых деформаций в любых плоских и пространственных системах, состоящих из шарнирно и жестко соединенных прямых и кривых брусьев.
Для определения линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице. При плоском изгибе интеграл Мора имеет вид
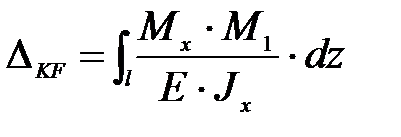 (4.4)
(4.4)
где 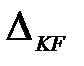 - искомое перемещение (линейное или угловое). Первый индекс К указывает точку и направление, в котором определяется перемещение, а второй – причину, вызывающую перемещение;
- искомое перемещение (линейное или угловое). Первый индекс К указывает точку и направление, в котором определяется перемещение, а второй – причину, вызывающую перемещение;
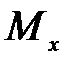 ,
, 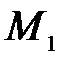 - аналитические выражения изгибающих моментов, соответственно от заданной нагрузки и единичной силы (единичного момента).
- аналитические выражения изгибающих моментов, соответственно от заданной нагрузки и единичной силы (единичного момента).
При вычислении интеграла Мора протяженность каждого участка  при постоянной жесткости сечения
при постоянной жесткости сечения 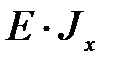 , определяется областью, в пределах которой закон изменения как «грузового», так и «единичного» моментов остается постоянным.
, определяется областью, в пределах которой закон изменения как «грузового», так и «единичного» моментов остается постоянным.
При воздействии на столб только силы Р прямолинейная форма равновесия центрально-сжатого стержня устойчива до тех пор, пока сжимающая сила Р не достигнет критического значения.
Критической силой 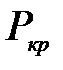 называется наименьшее значение сжимающей продольной силы, при котором прямолинейная форма стержня перестает быть устойчивой.
называется наименьшее значение сжимающей продольной силы, при котором прямолинейная форма стержня перестает быть устойчивой.
При потере устойчивости в упругой стадии работы стержня критическая сила вычисляется по формуле Эйлера
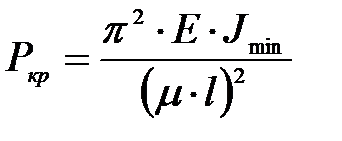 (4.5)
(4.5)
где Е – модуль продольной упругости материала стержня;
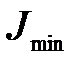 - минимальный главный центральный момент инерции поперечного сечения;
- минимальный главный центральный момент инерции поперечного сечения;
 - длина стержня;
- длина стержня;
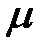 - коэффициент приведения длины, зависящий от способа закрепления концов стержня. При жестком закреплении стержня с одной стороны
- коэффициент приведения длины, зависящий от способа закрепления концов стержня. При жестком закреплении стержня с одной стороны 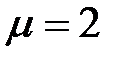 .
.
Практически переход сжимающей силы за критическое значение, производящий к продольному изгибу стержня, равносилен выходу стержня из строя. Поэтому допускаемая нагрузка должна быть обязательно меньше критической, так как продольный изгиб стержня недопустим.
Допустимую сжимающую силу определяют из условия устойчивости
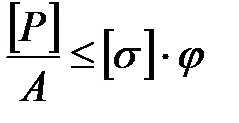 (4.6)
(4.6)
где А – площадь поперечного сечения;
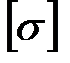 - допустимое нормальное напряжение материала;
- допустимое нормальное напряжение материала;
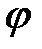 - коэффициент продольного изгиба, определяется в зависимости от материала и гибкости стержня.
- коэффициент продольного изгиба, определяется в зависимости от материала и гибкости стержня.
При воздействии на столб только момента 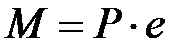 , его допустимое значение
, его допустимое значение 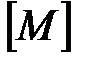 определяют из условия прочности при изгибе по формуле (4.2).
определяют из условия прочности при изгибе по формуле (4.2).
При совместном действии на столб сил Т, Р и момента пары сил М стержень подвергается совместному действию изгиба в плоскости действия сил Т и Р со сжатием. В опасной точке наиболее загруженного сечения (в защемлении) нормальное напряжение определяется по формуле
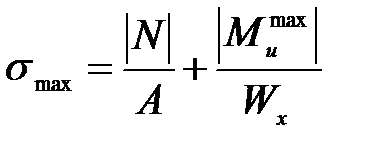 (4.7)
(4.7)
где 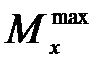 - изгибающий момент в защемлении при совместном действии силы Т и момента М;
- изгибающий момент в защемлении при совместном действии силы Т и момента М;
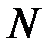 - продольная сила, равная Р;
- продольная сила, равная Р;
А - площадь поперечного сечения столба;
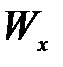 - осевой момент сопротивления поперечного сечения столба.
- осевой момент сопротивления поперечного сечения столба.
Расчет на прочность при изгибе со сжатием проводят по нормальным напряжениям, так как касательные напряжения, вызванные поперечной силой 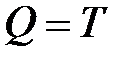 , незначительны.
, незначительны.
Условие прочности при изгибе со сжатием
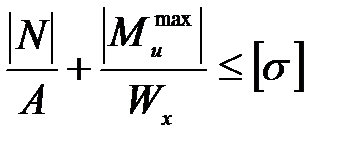 . (4.8)
. (4.8)
Дата добавления: 2015-02-25; просмотров: 5404;
