Ордината эпюры определяется по выражению

.

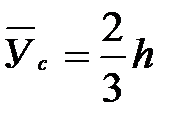Учитывая формулы (4.10) и (4.11), интеграл Мора

.

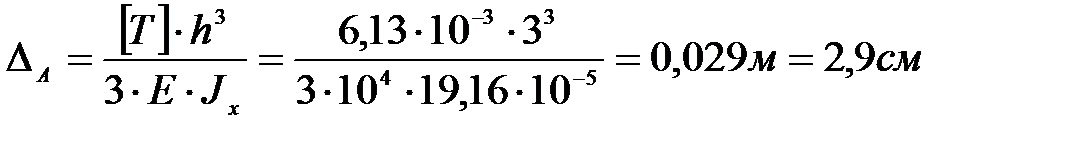На столб действует только вертикальная сила Р, вид нагружения при заданной нагрузке – центральное сжатие.

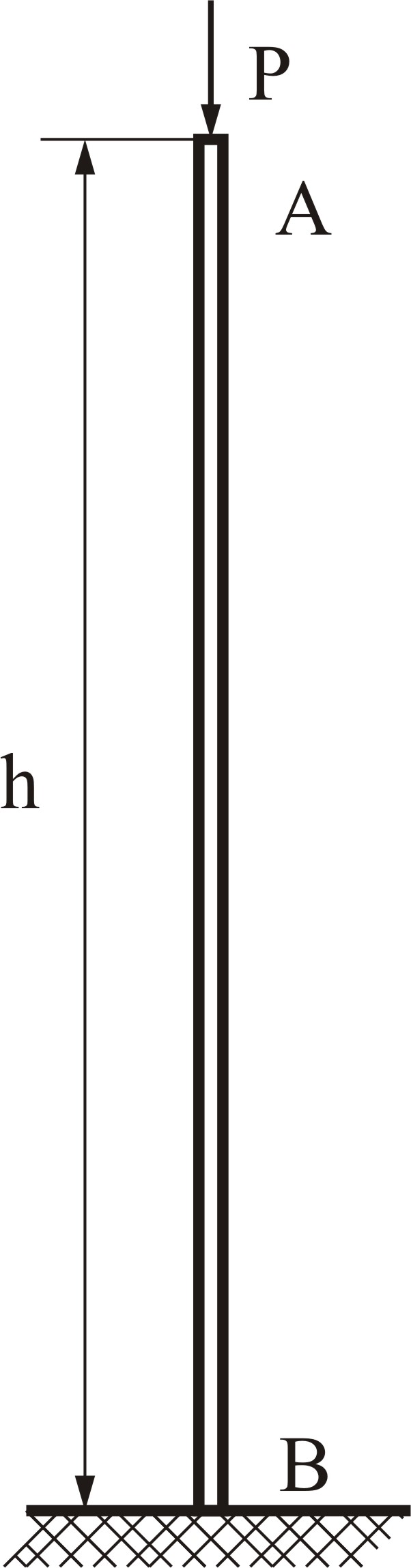
Рисунок 4.15

Определение критической силы .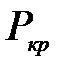

Критической называют силу, малейшее превышение которой, вызывает потерю устойчивого равновесия первоначальной формы тела. Критическую силу определяют в зависимости от гибкости стержня (величины, характеризующей склонность стержня к продольному изгибу).

Радиус инерции площади 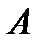поперечного сечения стержня определим по формуле

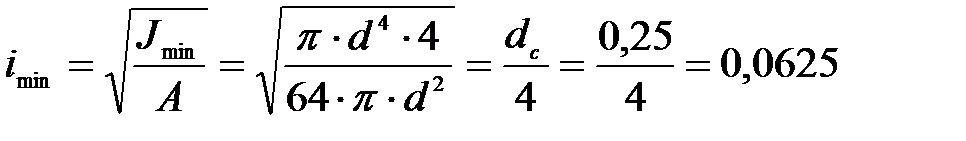м.

Площадь поперечного сечения столба (круга) определяется по формуле

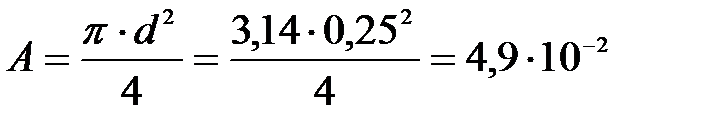м².

Тогда гибкость столба имеет вид

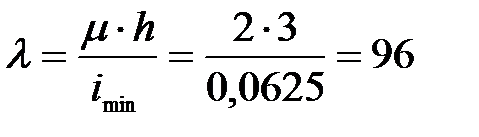
Для стержней большой гибкости (если гибкость стержня больше предельной гибкости) критическую силу определяют по формуле Эйлера. Для дерева предельная гибкость 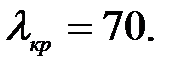В нашем случае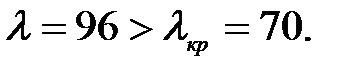

Критическая сила по формуле Эйлера:

.

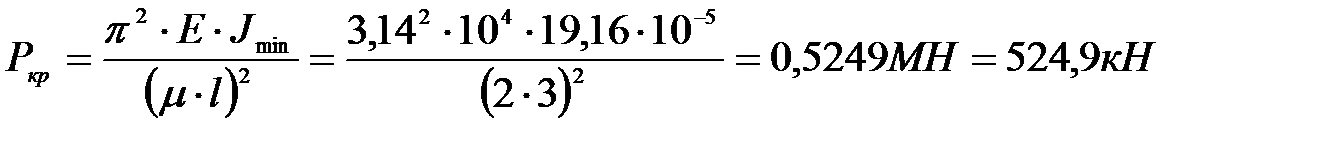Коэффициент 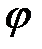определяют в зависимости от гибкости стержня и его материала по таблице Г.1 (приложение Г), с помощью линейной интерполяции:

при ;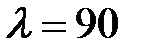

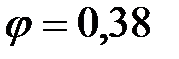при ;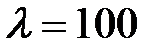

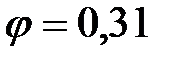при .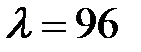

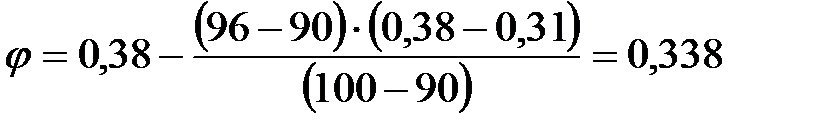Из условия устойчивости допускаемое значение сжимающей силы 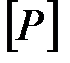определяется по выражению:

.

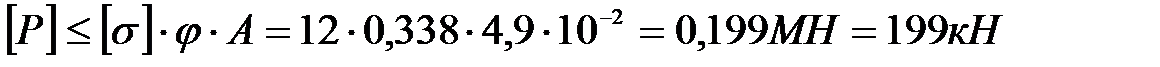На столб действует только сосредоточенный момент М

При заданной нагрузке вид нагружения – плоский изгиб, изгибающий момент по всей высоте столба постоянный и во всех сечениях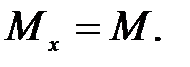

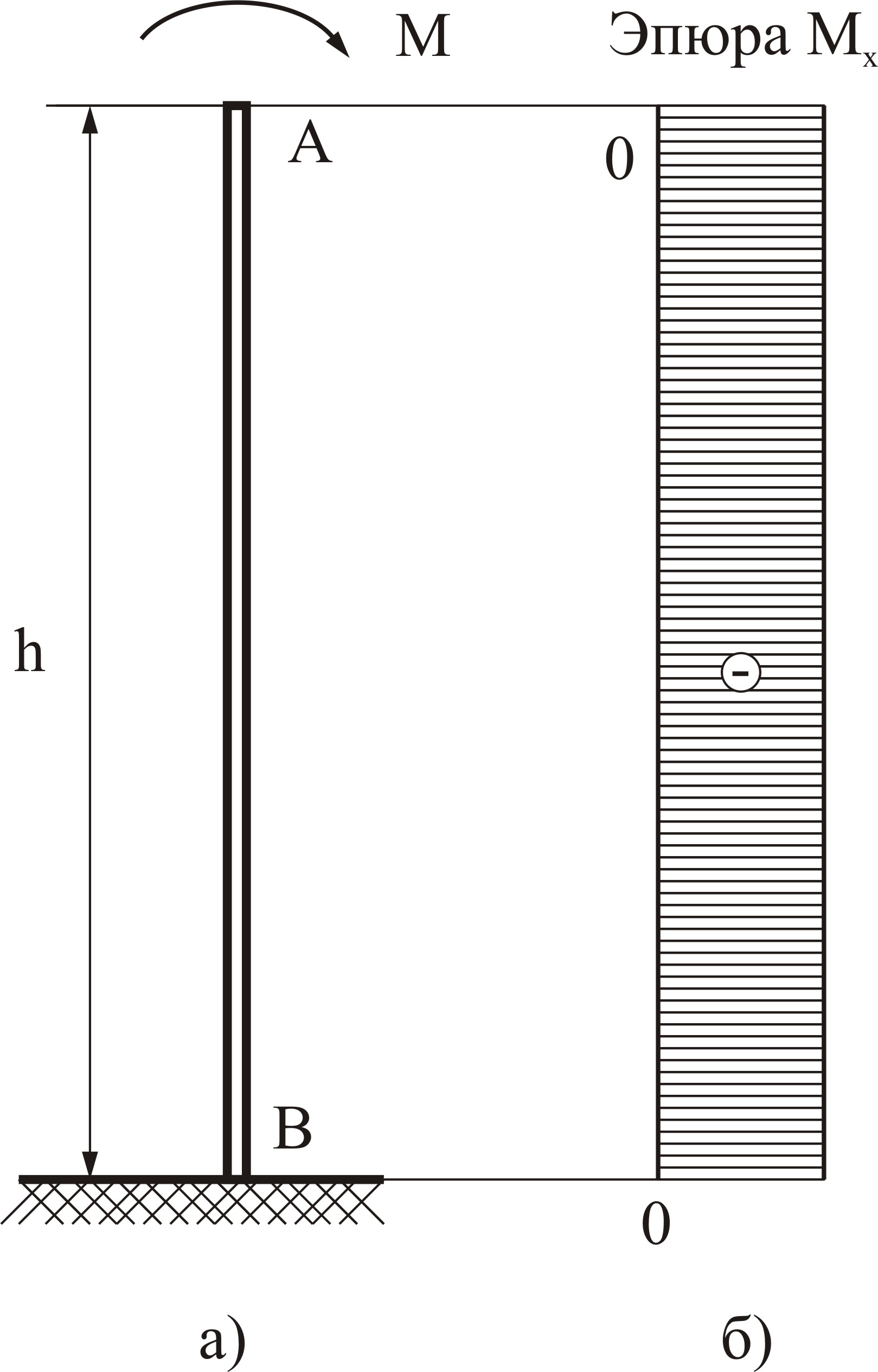
Рисунок 4.16

Допускаемое значение момента 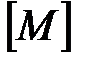определим из условия прочности при изгибе

.

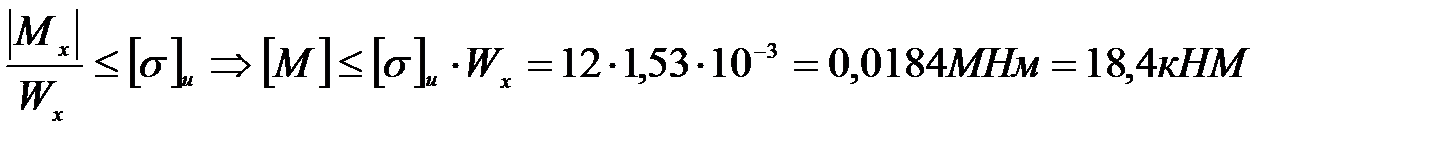4.2.4 На столб действуют все нагрузки Т, Р и М

Вид нагружения – изгиб со сжатием.

Приняв 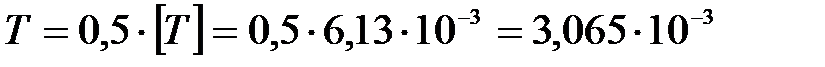МН.

МН.

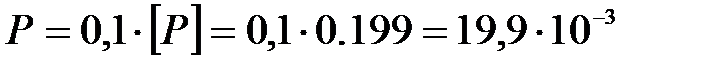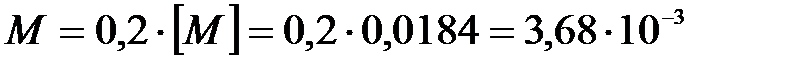МН·м.

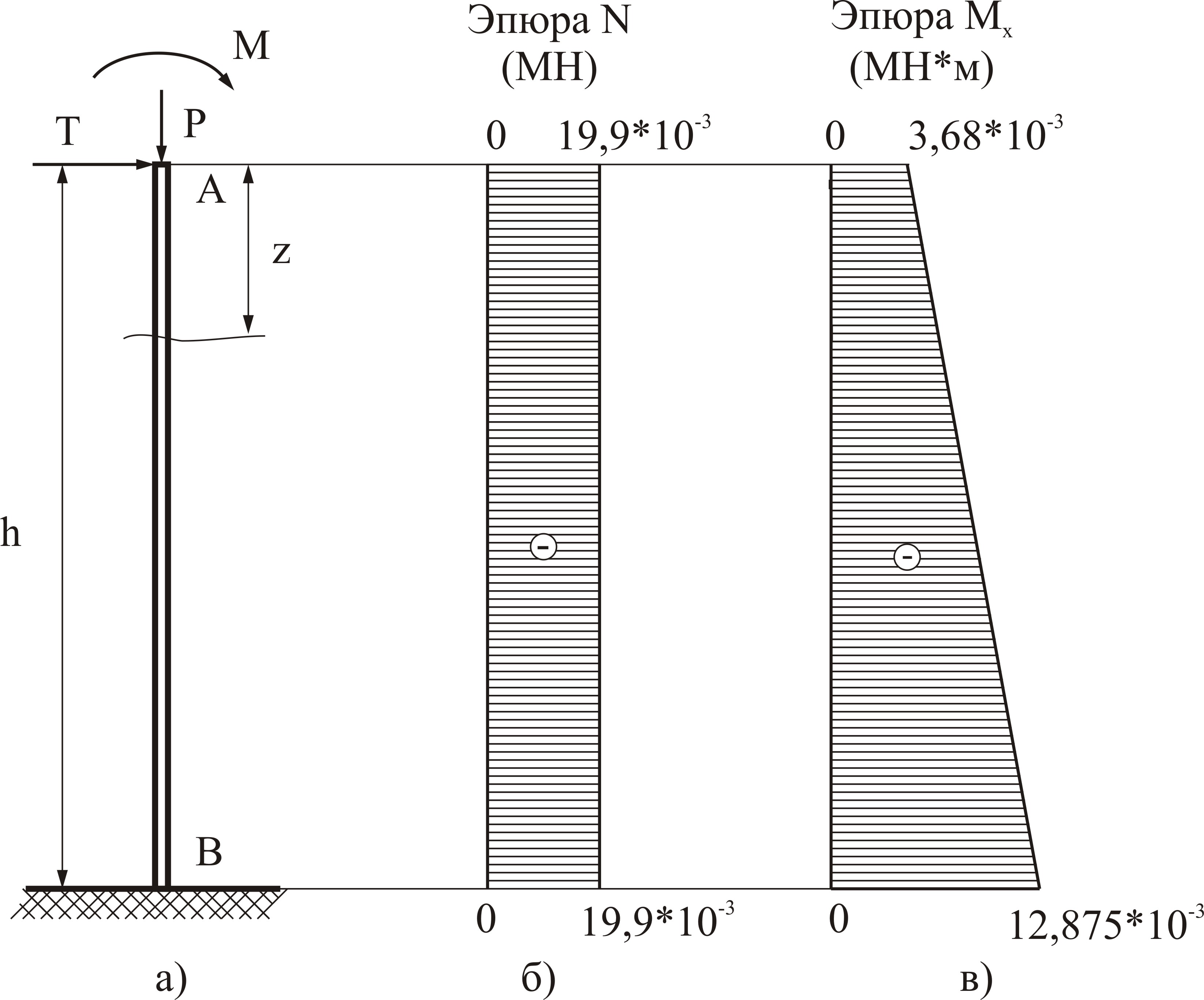
Рисунок 4.17

При изгибе с растяжением-сжатием проверочный расчет на прочность производится из условия прочности по нормальным напряжениям по формуле (4.5).

В произвольном сечении стержня: 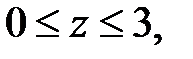продольная сила 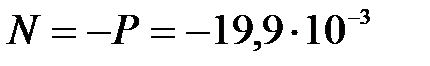МН, изгибающий момент ,

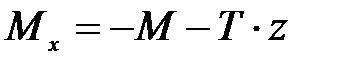при 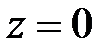: 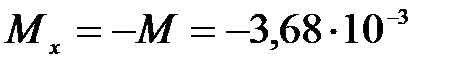МН·м;

при 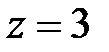: 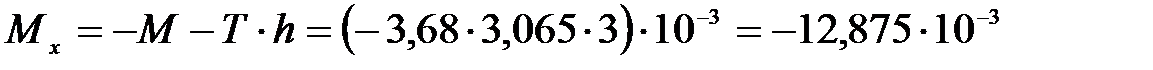МН·м.

Используя расчеты, строим эпюры внутренних усилий, представленных на рисунке 4.7.

Опасным является сечение у основания столба, в котором нормальное напряжение определим по формуле (4.4)

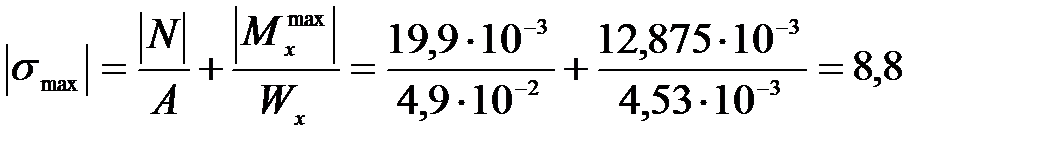МПа.

Подставив в условие прочност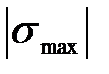и и 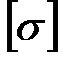, получим

.

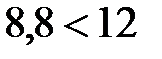Вывод: условие прочности выполняется, следовательно, столб прочный.

ЛАБОРАТОРНАЯ РАБОТА №3