Лабораторная работа № 5. Влияние надреза на механические свойства стали
Влияние надреза на механические свойства стали
5.1. Цель работы: ознакомиться с влиянием остроты надреза на механические свойства, стали.
5.2. Теоретическая часть
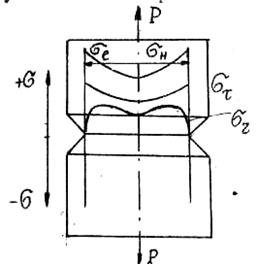
Выявление механических свойств при статических испытаниях обычно осуществляется на гладких (постоянного сечения) образцах. Однако в критических условиях детали конструкций имеют переходы в сечениях, отверстия, резьбу и неровности, что очень сильно отражается на реальной прочности и особенно пластичности материала деталей. Перенесение для таких деталей характеристик механических свойств, полученных при испытании стандартных гладких образцов, в ряде случаев является неправомерным. Это объясняется тем, что неровности в деталях приводят к концентрации напряжений и изменению напряженного состояния металла в части детали, где имеет место изменение сечения, которое называется концентратором напряжений. На рис.5.1 показаны схемы эпюр напряжений, возникающих по сечению в гладком образце и в надрезанной части образца с концентратором напряжений.
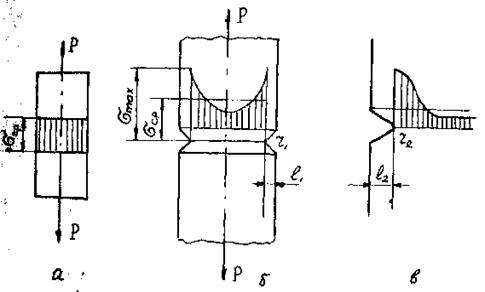
Рисунок.5.1. Эпюры напряжений при растяжении гладкого (а), остро надрезанного (б) и образца (в) с "мягким" надрезом
Концентрация напряжений (К) тем больше, чем острее дефект и больше его длина, что выражается следующей формулой:
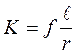
где 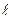 - длина надреза (иного дефекта); r - радиус закругления в вершине дефекта.
- длина надреза (иного дефекта); r - радиус закругления в вершине дефекта.
Величина r может быть очень малой, т.е. трещина очень острая, но она не может быть меньше 0,1Нм (10 мм), т.е. меньше, чем диаметр атома, и надо полагать, что минимальный радиус трещин составляет примерно 10-5 мм. Отсюда для такой предельно острой трещины величина К составляет (в зависимости от длины):
| К | |||
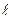 , мм , мм
| 0,1 | 0,01 |
Это значит, что если такая предельно острая трещина доросла до ℓ мм, то в ее вершинах напряжение в 600 раз больше среднего. В деталях с надрезом (рисунок 5.2) возникает трехосное напряженное состояние, увеличивающее склонность к хрупкому разрушению (рисунок 5.2). Чем острее и глубже надрез, тем выше неоднородность напряжения в сечении. Для пластичных металлов при нагружении происходит местная пластическая деформация, в результате чего происходит изменение напряженного состояния: максимум осевых напряжений перемещается вглубь образца и опасность хрупкого разрушения таких материалов меньше, чем высокопрочных.
σ 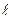 - распределение по сечению осевых нормальных напряжений;
- распределение по сечению осевых нормальных напряжений;
σr - распределение по сечению радиальных напряжений;
στ - распределение тангенциальных касательных напряжений.
Рисунок 5.2. Схема распределения напряжений в образце с надрезом.
У весьма пластичных материалов выравнивание может произойти ложью, разрыв образца в этом случае произойдет тогда, когда осевое напряжение по всему сечению достигнет истинного предела прочности.
Для хрупких и мало пластичных материалов, обладающих высоким сопротивлением пластической деформации, пластическая деформация не получает должного развития и выравнивание напряжений по сечению не происходит. Поэтому у дна надреза достигается напряжение, соответствующее истинному сопротивлению отрыва.
5.3. Порядок проведения работы
5.3.1. Подготовить к испытанию 3 образца из стали 45 (один гладкий, второй с надрезом 150 °, третий с надрезом 60˚).
С помощью лупы с точностью до +- 0,1мм измерить диаметр у дна надреза и рабочую длину 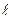 p = 5d , отметить кернами на поверхности образцов. Зарисовать эскизы образцов (рисунок 7.3).
p = 5d , отметить кернами на поверхности образцов. Зарисовать эскизы образцов (рисунок 7.3).
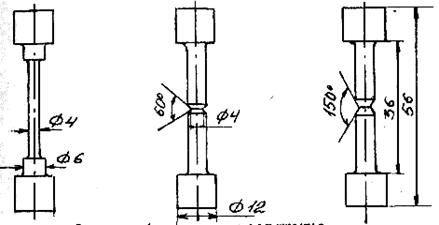
Рисунок 5.3. Эскизы образцов для испытаний на растяжение
5.3.2. Испытать образцы с записью диаграммы растяжения.
5.3.3.На разрушенных образцах измерить диаметры в месте разрушения с помощью лупы и измерить конечную длину ℓк между кернами.
5.3.4. Результаты замеров до и после испытания занести в таблице 5.1.
5.3.5. По диаграмме растяжения определить Р 0,2 (или Pm, если есть площадка текучести), Рв, Рк и ∆ℓ с учетом масштаба диаграммы, как показано на рисунок 7.4. Для определения Р0,2 на оси ∆ℓ откладываем отрезок ∆ℓ0,2 = ℓp∙ 0.002 M ( ℓp - расстояние между корнами по длине образца, М - масштаб удлинения).
Из конца отрезка проводим прямую параллельно участку пропорциональности до пересечения с диаграммой. Точка пересечения m дает P 0,2, точка к – Pк. Значения нагрузок заносим в табл.5.1.
Таблица 5.1. Значения размеров образцов и нагрузок при испытании на растяжение
| Тип образцов | d, мм | dк, мм | ℓo, мм | ℓк, мм | Fo, мм2 | Fк, мм2 | ∆ℓ, мм | M∆ℓ | Pв, Н | Mp | P0.2, Н | Pк, Н |
| 1.Гладкий | ||||||||||||
| 2.Надрез 150º | ||||||||||||
| 3.Надрез 60º |
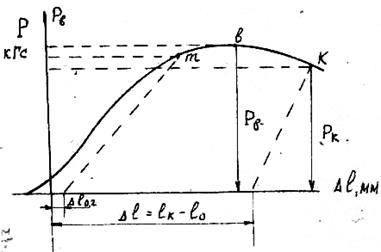
Рисунок 5.4. Диаграмма растяжения
5.3.6. По данным таблицы 5.1 произвести расчет характеристик механических свойств. Значения механических свойств занести в таблицу 5.2.
Определить и занести в таблицу 5.2. отношение
σн / σгл
Таблица 5.2. Значения характеристик механических свойств
| Тип образцов | δ5, % | Ψ,% | σ0.2, МПа | σВ, МПа | Sк, МПа |
| 1.Гладкий | |||||
| 2.Надрез 150º | |||||
| 3.Надрез 60º |
5.3.7.Сопоставить полученные данные и сделать выводы по влиянию угла надреза.
5.4. Требования к отчету
В отчете по работе должны быть представлены в виде схем диаграммы деформации, результаты их анализа, сведенные в таблицы и выводы.
5.5 Вопросы для подготовки
1. Почему необходимо учитывать влияние концентратора напряжет!» на механические свойства металлов?
2. Как влияет надрез на характер напряженного состояния по сечению?
3. Чем можно объяснить отсутствие связи между твердостью и пределом прочности на разрыв хрупких материалов? (За основу следует взять физическую сущность этих характеристик материала).
4. Как влияет острота надреза на прочность и пластичность?
5. Почему σ0,2, σ Т, σв могут строго характеризовать сопротивление материалов разрушению
Дата добавления: 2015-02-25; просмотров: 878;
