Прямая геодезическая задача

Дано: координаты точки 1(х₁; у₁), горизонтальное расстояние между точками 1 и 2 (d), дирекционный угол линии 1-2 (a).

Найти: координаты точки 2 (х₂; у₂).

На рис. 13,а видно, что

х₂ = х₁ + Δх, у₂ = у₁ + Δу.

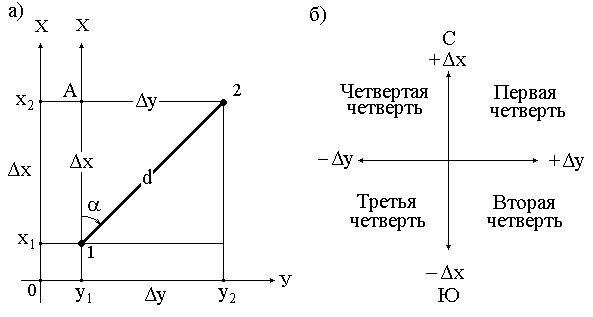
Рис. 13. Прямая геодезическая задача

Из прямоугольного треугольника 1А2 следует, что

Δх = d×cosα, Δу = d×sinα.

Тогда х₂ = х₁ + d×cosα, у₂ = у₁ + d×sinα.

Координата последующей точки равна координате предыдущей точки плюс приращение координаты. На практике пользуются следующими формулами:

х₂ = х₁ ± d×cosr, у₂ = у₁ ± d×sinr.

Пример. Дано: х₁ = 100,00 м; у₁ = 200,00 м; α = 210º;

d = 150,00 м. Найти: х₂, у₂.

Решение.Дирекционный угол линии составляет α = 210º, следовательно, линия находится в третьей четверти. Румб линии r = ЮВ:30º. В третьей четверти приращения координат отрицательные, поэтому

х₂ = х₁ – d×cosr = 100,00 – 150,00×cos30º =

= 100,00 – 150,00×0,86602 = – 29,90 м;

у₂ = у₁ – d×sinr = 200,00 – 150,00×sin30º =

= 200,00 – 150,00×0,50000 = +125,00 м.