Лекция 4. Законы движения воздуха в горных выработках
1 Давление и депрессия движущегося воздуха
2 Воздуховоды и их параметры
3 Режимы движения воздуха
4 Типы воздушных потоков
5 Уравнение Бернулли
6 Сопротивление горных выработок
7 Единицы сопротивления горных выработок
8 Вентиляционная характеристика горных выработок
9 Способы изменения сопротивления горных выработок
ЗАКОНЫ ДВИЖЕНИЯ ВОЗДУХА В ГОРНЫХ ВЫРАБОТКАХ
1 ВИДЫ ДАВЛЕНИЯ В ДВИЖУЩЕМСЯ ВОЗДУХЕ. ДЕПРЕССИЯ
Виды давления. Любое движение воздуха происходит в пределах земной атмосферы, причем так, что над областью движения всегда находятся слои воздуха, оказывающие давление на каждый объем движущегося воздуха. Таким образом, аэродинамическое давление - давление вышележащих слоев воздуха - является первой составной частью полного давления движущегося воздуха.
Из механики известно, что любое движущееся материальное тело обладает кинетической энергией и что в случае встречи тела с какой-либо преградой оно окажет на преграду давление, которое будет зависеть от кинетической энергии тела. Являясь материальной субстанцией, движущийся воздух полностью подчиняется отмеченным законам.
Если в поток воздуха поместить какое-либо тело, например пластину, то движущийся воздух будет оказывать на нее давление, определяемое его кинетической энергией. Это давление называется динамическим или скоростным. Таким образом, динамическое (скоростное) давление является составной частью полного давления движущегося воздуха.
Энергетическая интерпретация давления. Рассмотрим существующие в движущемся воздухе давления с энергетической точки зрения. Выделим в неподвижной атмосфере некоторый объем воздуха, находящийся под аэростатическим * давлением р. Если вокруг него создать разрежение, то рассматриваемый объем начнет расширяться до тех пор, пока давление внутри него не будет равно давлению снаружи. При этом расширяющимся объемом воздуха будет совершена работа. Следовательно, уменьшение статического давления воздуха сопровождается выполнением определенной работы. Данное обстоятельство свидетельствует о том, что статическое давление-является одной из форм энергии, а именно потенциальной энергией, которая при определенных условиях может переходить в работу. Поэтому статическое давление воздуха можно определить как потенциальную энергию, характеризующую работу, которую может совершить данный объем воздуха при его расширении до конечного давления
р = 0.
Поскольку причиной динамического давления является движение воздуха, очевидно, что оно характеризует кинетическую энергию воздуха. Кинетическая энергия тела массой М, движущегося со скоростью и,
EK = Mu2/2
а отнесенная к единице его объема
ек = yu2/2g,
где у—: удельный вес тела; g — ускорение свободного падения.
Если принять, что вся кинетическая энергия переходит в динамическое давление, т. е. что Pдин = ек, то
Рдин=yu2/2g
Поскольку скорость и в, общем переменна в пространстве, динамическое давление является функцией точки. В частности, оно изменяется в поперечном сечении выработки, в то время как статическое давление во всех точках поперечного сечения практически одинаково.
Полная энергия единицы объема воздушного потока равна сумме его потенциальной и кинетической энергий. Поскольку потенциальная энергия потока характеризуется1 его статическим давлением рст, а кинетическая — динамическим рщш, то. полное давление
Рп = Рст+Рдин
Депрессия. Депрессией в рудничной вентиляции называется разность давлений. Разность статических давлений называется статической депрессией, разность скоростных давлений – скоростной депрессией (или разностью скоростных давлений), разность полных давлений – полной депрессией.
2 ВОЗДУХОВОДЫ С ПЕРЕМЕННЫМИ ПО ДЛИНЕ ПАРАМЕТРАМИ
Для трубопроводов больших длин, особенно с небольшими сроками службы, начинают сказываться различия в коэффициентах а и к для начального и
конечного его участков. Кроме того, из-за больших утечек расход воздуха у вентилятора в несколько раз может превышать расход в конце трубопровода, вследствие чего можно было бы иметь воздуховод большего диаметра у вентилятора и меньшего — у забоя. При перепадах давления но длине трубопровода h≥300 кгс/м2 существенной оказывается и сжимаемость воздуха.
В связи с этим представляет интерес обобщение полученных зависимостей на случай переменных значений диаметра трубопровода dТ (x), коэффициента аэродинамического сопротивления а (х), коэффициента неплотности к (х), а также переменной плотности воздуха р (х). Что вполне допустимо для трубопроводов значительной длины, перепишем это выражение следующим образом:
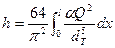 (1)
(1)
Тогда вместо уравнения будем иметь
PQPQ-n(x)p2Q=0 (2)
В общем случае уравнение (2) не интегрируется и его исследование затруднено. Однако в важном для практики случае, когда п (х) меняется медленно (адиабатически), можно получить адиабатическое решение этого уравнения в виде:
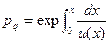 (3)
(3)
Подставляя выражение (3) в уравнение (2) получим соотношение для и (х)
u\+n(x)u3-1=0 (4)
которое является уравнением Абеля пёрвого рода.
Учитывая медленное изменение функции п (х), воспользуемся методом последовательных приближении, чтобы построить выражение для и (х). В качестве нулевого приближения принимаем и'о = 0, тогда
u0= 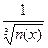 (5)
(5)
Дифференцируя выражение (5) и подcтавляя его в уравнение (4), получим следующее приближение:
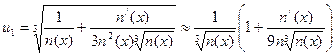 (6)
(6)
и так далее.
Этот процесс сходится, если |n®(x)|<|n(R-1)(x)| для всех R = 1, 2, . . .
Из выражения (6) получаем оценку для границ возможного использования приближения (5)
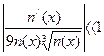 (7)
(7)
или развернутом виде
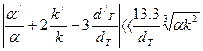 (8)
(8)
 Анализ выражения (8) показывает, что решение (5) приемлемо практически для всех случаев шахтных воздуховодов.
Анализ выражения (8) показывает, что решение (5) приемлемо практически для всех случаев шахтных воздуховодов.
Таким образом, для расчета воздуховода с переменными по длине параметрами имеем следующие формулы:
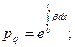 (9)
(9)
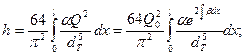 (10)
(10)
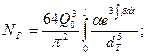 (11)
(11)
где iVr — гидравлическая мощность, теряемая "в трубопроводе.
Наличие утечек воздуха в трубопроводе приводит к значительному повышению давления и мощности по сравнению с плотным трубопроводом, в котором при постоянных значениях Qo, a, dT величины h и Nr линейно зависят от длины; в трубопроводе с утечками эти зависимости сугубо нелинейны. Однако можно построить такой трубопровод, например с переменным диаметром, у которого несмотря на утечки указанные зависимости будут линейными.
Пренебрегая зависимостью коэффициента, а от диаметра трубопровода, из формулы (10) найдем
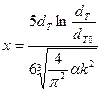 (12)
(12)
3 РЕЖИМЫ ДВИЖЕНИЯ ВОЗДУХА В ШАХТАХ
Движение воздуха по любому каналу может быть спокойным, характеризующимся обычно малыми скоростями, параллельными траекториями частиц и отсутствием перемешивания между отдельными слоями потока,— ламинарным либо бурным, характеризующимся беспорядочным перемещением отдельных частиц и хаотическим перемешиванием между слоями потока, — турбулентным.
Если средняя скорость потока постоянна, то скорость и давление потока в точке при ламинарном движении не изменяются во времени, т. е. движение является стационарным. При турбулентном движении даже в случае постоянства его средней скорости точечные характеристики потока изменяются во времени, пульсируют, вследствие чего лишь осредненные по времени их значения оказываются постоянными, а движение является квазистационарным.
Пульсации турбулентного движения являются проявлением существующих в нем вихрей самых различных размеров.
Основное различие между ламинарным и турбулентным режимами движения состоит в механизме переноса субстанции: в ламинарном этот перенос обусловлен обменом молекулами между слоями потока, в турбулентном — обменом объемами. Турбулентный перенос во много раз интенсивнее молекулярного.
Режим движения воздуха в выработке можно определить визуально, например, при помощи тонких струек дыма: если струйки сохраняются на значительном расстоянии от источников — движение ламинарное, быстрое их перемешивание с воздухом указывает на турбулентное движение. Определить режим движения воздуха в выработке можно также при помощи специального критерия — числа Рейнольдса Re:
Re = uD/v, (1)
где и — средняя скорость движения воздуха в выработке; D — гидравлический диаметр выработки; v — кинематическая вязкость воздуха.
Гидравлический диаметр определяется по формуле
D = 4S/P, (2)
где S — площадь поперечного сечения выработки; Р – eё периметр. Число Re безразмерно.
Экспериментально установлено, что в гладких трубах при Re = = 2300 устойчивым является турбулентное движение, т. е. при этом даже небольшие возмущения потока (внесение в поток постороннего тела колебания стенки и т. п.) вызывают переход ламинарного движения в турбулентное, причем :; дальнейшем движение остается турбулентным даже при устранении .возмущений, При Re< <2300 устойчиво ламинарное движение.
В шахтных выработках критическое значение числа Re=1000-1500. Следовательно, минимальная скорость, при которой движение еще остается турбулентные, например при D = 2,5 м и v =1,5*105 м2/с, будет 0,006—0,01 м/с. Правила безопасности требуют, чтобы скорость движения воздуха в выработках была не менее 0,25 м/с. Фактические скорости движения воздуха в современных шахтах значительно выше. Поэтому в выработках, проветриваемых деятельной вентиляционной струей, движение воздуха, как правило, турбулентное.
При фильтрационном движении воздуха по узким каналам (просачивание воздуха через целики, перемычки, уплотненные участки обрушений в выработанном пространстве и т. п.), происходящем обычно при низких скоростях, часто наблюдается ламинарный режим движения.
Переход ламинарного движения в турбулентное в отдельной точке происходит почти мгновенно, однако в пространстве между источником возмущения и сечением потока, где движение турбулентное, лежит переходная область, лишь частично заполненная турбулентными вихрями. Наблюдения показывают что в очень шероховатых воздухопроводах, к которым относится и большинство горных выработок, турбулентность зарождается непосредственно у выступов шероховатостей, в то время как при гладких стенках развитие турбулентности может происходить от вихрей, заносимых ядром потока. Наконец,
Вдоль потока режим движения может изменяться вследствие увеличения или уменьшения диаметра канала. Отмеченные обстоятельства приводят к тому, что при движении воздуха возможно существование промежуточных режимов, при которых поток состоит из ряда расположенных по его длине областей с турбулентным и ламинарным режимами. В шахтных условиях промежуточные режимы наблюдаются, например, при движении воздуха в выработанном пространстве, через слой угля в бункерах, через герметизирующие сооружения.
Однако даже при вполне развитом турбулентном движении у стенок воздухопровода сохраняется тонкий слой (ламинарный пограничный слой), в пределах которого движение ламинарно. При малых числах Re толщина ламинарного слоя (рис 1,а) большая и в него оказываются погружёнными все выступы шероховатости. При этом они оказывают минимальное сопротивление по току. С увеличением числа Re
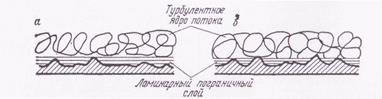
Рис. 1. Ламинарный пограничный слой: а— при малом числе Re; б — при большом числе Re
толщина ламинарного слоя уменьшается, выступы шероховатости внедряются в турбулентное ядро потока, оказывая последнему все возрастающее сопротивление (рис. 1,6).
4 ТИПЫ ВОЗДУШНЫХ ПОТОКОВ В ГОРНЫХ ВЫРАБОТКАХ
Все воздушные потоки в выработках можно разделить на два основных типа: ограниченные потоки, или потоки с твердыми границами, и свободные, не имеющие твердых границ, называемые также свободными струями.
К ограниченным потокам относятся, например, потоки воздуха в штрекообразных выработках на прямолинейных участках при постоянном их сечении. В этом случае потоки имеют твердые границы в виде стенок выработок.
Свободные струи образуются, когда воздушный поток из воздухопровода ограниченного сечения выходит в неограниченное (достаточно большое) пространство. Воздушная струя при этом распространяется в заполненном воздухом пространстве и не имеет твердых границ.
К свободным струям относятся, например, потоки воздуха, выходящие из штрека в камеру большого сечения, из трубопровода в выработку и т. п. В зависимости от формы поперечного сечения свободных струй они могут быть круглыми и плоскими. Если на каком-либо участке свободная струя соприкасается с твердой поверхностью и не получает полного развития, она называется неполной.
Ограниченные потоки и свободные струн движутся по существенно различным законам. Так, в ограниченных потоках происходит падение давления в направлении движения, в свободных же струях давление постоянно и равно давлению окружающего воздуха; ограниченные потоки имеют логарифмический профиль скоростей, свободные струи— профиль в виде кривой Гаусса; кроме того, эти потоки различны по характеру протекания диффузионных процессов.
Знание законов движения ограниченных потоков необходимо для организации вентиляции выработок типа штреков, квершлагов, лав, а законов движения свободных струй — для организации вентиляции камерообразных выработок, призабойной части тупиковых выработок и др.
5 УРАВНЕНИЕ БЕРНУЛЛИ
Закон сохранения энергии. Для случая движения воздуха закон сохранения энергии может быть сформулирован следующим образом [изменение энергии произвольного объема воздуха за некоторый промежуток времени при его движении' равно сумме количества сообщенного ему тепла и работы приложенных к объему внешних сил за то же время, т. е.
∆Eвн+∆Еп+∆Ек=I∆Q+∆A (1)
где ∆Eвн — изменение внутренней энергии данного объема воздуха, определяемой кинетической энергией движения молекул и потенциальной энергией их взаимодействия; ∆Еп — изменение потенциальной энергии этого объема, определяемое его перемещением по вертикали; ∆Ек — изменение кинетической энергии объема;
I— механический эквивалент тепла; AQ— количество тепла, полученное (отданное) данным объемом воздуха; ∆A — работа внешних сил.
Внешними силами при движении воздуха по выработке являются силы трения о ее стенки и силы статического давления, приложенные к поверхности рассматриваемого
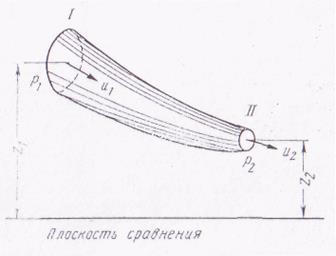
Рис. 1 - Элементарная струйка тока объема.
В случае адиабатического движения несжимаемой жидкости которой можно считать воздух при существующих в шахте давлениях, ∆Eвн =∆Q =0. При этом условии для установившегося движения элементарной струйки воздуха соотношение (1) может быть записано в виде
(1/γ)dp + dz + du2 /2g + dh = 0, (2)
где р — давление воздуха; z — аппликата центра тяжести сечения струйки относительно произвольной горизонтальной плоскости сравнения; u — скорость воздуха в рассматриваемом сечении струйки; h — работа внешних сиk отнесенная к единице массы воздуха.
Уравнение (2) называется уравнением Вернулли в дифференциальной форме (по имени русского ученого Даниила Бернулли, впервые получившего это соотношение в 1738 г.).
Интегрируя выражение (2) вдоль струйки от сечения I до сечения II (рис.1) при γ = const, получим
(P1 – Р2) +γ(z1 - z2)+γ (u12+u22)/2g = h. (3)
Коэффициенты k1 и k2 в уравнении (3) называются коэффициентами кинетической энергии и учитывают неравномерность распределения скоростей движения воздуха в сечениях I и II выработки. Их можно определять по формулам: для круглых штрекообразных выработок
k = I +213a;
для штрекообразных выработок, закрепленных неполными рамами
k = 0,810 + 282а,
где а — коэффициент трения.
Важным следствием из уравнения Бернулли является тот факт, что при h = const изменение и в сечении вызывает обратное изменение р. Действительно, при увеличении u2 давление р2 должно уменьшаться, чтобы было соблюдено условие h = const. Справедливо и обратное заключение. Следовательно, увеличение скорости движения воздуха в сечении (например, вследствие его уменьшения) вызывает уменьшение в нем статического давления, и наоборот.
Уравнение Бернулли является одним из основных уравнений рудничной аэродинамики, ибо, являясь математической формулировкой закона сохранения энергии, оно объединяет все основные величины, необходимые для решения любой аэродинамической задачи.
6 ЗАКОН СОПРОТИВЛЕНИЯ ГОРНЫХ ВЫРАБОТОК
Под законом сопротивления в рудничной вентиляции понимается зависимость между депрессией h и средней скоростью u (или количеством Q) воздуха в выработке
h = R1un = R2Qn, (1)
где R1 и R2 — коэффициенты пропорциональности; n — показатель степени, зависящий от режима движения; при турбулентном режиме n = 2; при ламинарном n= 1.
В горных выработках при турбулентном режиме движения n = 2, при малых скоростях (Re = 2*104-З*104)n ≈1,8.
Механизм действия сил сопротивления. Выше отмечалось, что при движении воздуха в потоке появляются силы трения вследствие эффекта прилипания и вязкости. Поскольку стенки горных выработок шероховаты, движущийся вдоль, них воздух оказывает также давление на погруженные и поток выступы шероховатости, вследствие чего появляется вторая составляющая силы сопротивления— сила давления. Шероховатость горных выработок обычно относительно равномерно распределена как по их длине, так и по периметру поперечного сечения. В результате силы трения и силы давления распределяются по всей поверхности выработки и везде проявляются совместно. На практике обе силы оценивают совместно. Результирующая сила при этом с определенной условностью называется силой трения, а .вызываемое ею сопротивление — сопротивлением трения.
В условиях горных выработок основное сопротивление движению воздуха оказывают элементы крепи. Поток воздуха, подойдя к элементу крепи, поджимается в результате чего лобовая часть элемента воспринимает динамическое давление набегающего потока. За элементом крепи вследствие срыва потока образуются свободная струя и мертвая зона, заполненная массами воздуха, находящимися в вихревом движении. Далее в зависимости от расстояния до следующего элемента крепи либо может находиться область ограниченного потока, либо может вновь начинаться его поджатие. Основными составляющими сопротивления здесь являются, давление на лобовую часть элемента крепи, диссипация (рассеивание) энергии вследствие трения в вихрях застойной зоны, трения о поверхность крепи и стенки выработки. При сплошном расположении элементов крепи размеры застойных зон минимальны. По мере увеличения расстояния между элементами крепи увеличивается объем вихревых зон и, следовательно, потеря энергии в них. Одновременно увеличивается область лобовой крепи, испытывающая давление потока. С появлением участка ограниченного потока вихревые зоны достигают наибольшего развития и потеря энергии в них, а также силы давления на крепь достигают максимума. При дальнейшем увеличении расстояния между элементами крепи их число, а также число полностью развитых вихревых зон на единицу выработки уменьшаются, а сопротивление каждого элемента остается постоянным; увеличение трения о стенки на участках ограниченного потока при этом не может компенсировать снижение сопротивления, вызываемого уменьшением числа элементов крепи. В результате после первоначального увеличения сил сопротивления (на единице длины) до некоторого максимума минимальное сопротивление достигается при расстояниях между элементами крепи, примерно равных 5—6 их высотам.
7 ЕДИНИЦЫ СОПРОТИВЛЕНИЯ ГОРНЫХ ВЫРАБОТОК
Размерность аэродинамического сопротивления
[R] = [h/Q2] = Н*с2/м8
Единица с такой размерностью называется киломюргом (kμ) , или большой единицей сопротивления (б.е.с.). Эта единица распространена в РФ, Франции и ГДР (в ГДР ее называют вейсбах ω). На практике часто используют единицу, в тысячу раз меньшую, - мюрг (μ), или малую единицу сопротивления (м. е. с.).
Если сопротивление выработки выражается в киломюргах R, а в мюргах r, то
R =1000 r
В Великобритании применяется единица аткинcон (атк),. равная сопротивлению выработки при h=1 фут/фут2 и Q = 1000 фут3/с, а также практическая единица (п. e.)
Соотношение между единицами:
lkμ = lω = 164 атк = 8,75 п. е.
В вентиляторостроении и в меньшей мере в шахтной вентиляции применяется еще одна единица сопротивления — эквивалентное отверстие А, под которым понимается круглое отверстие в тонкой стенке, сопротивление которого равно сопротивлению шахты или выработки при одинаковом расходе воздуха. Это понятие вошло в шахтную вентиляцию из области шахтного вентиляторостроения, где для испытания вентиляторов используют тонкие металлические пластины с круглыми отверстиями.
8 ИЗМЕНЕНИЕ СОПРОТИВЛЕНИЯ ГОРНЫХ ВЫРАБОТОК
Поскольку главным источником дополнительных потерь энергии в местных сопротивлениях являются вихревые зоны, основные меры снижения местных сопротивлений заключаются в придании выработкам таких форм, при которых размеры этих зон были бы минимальными. Этого можно достичь применением плавных переходов от одного сечения выработки к другому, плавных поворотов, особенно со скруглением кромок; устранением (отшивкой, заполнением) «кутков», скруглением мест входа воздуха в трубопроводы и выработки; установкой направляющих лопаток на поворотах; уменьшением длины участков местных сопротивлений (каналов вентиляторов и т. п.). Наименьшие потери энергии потоке при расширении выработки бывают, когда угол раскрытия составляет 5—8°, а при ее сужении, когда он не превышает 5°. В случае скругления кромок входа в трубопровод радиусом 0,1 D (D — диаметр трубы) и снижается в 10 раз, а в случае скругления только внутренней кромки угла поворота радиусом, равным 1/3 b (b — ширина выработки), — почти в 2 раза.
Уменьшению местных сопротивлений способствует также снижение шероховатости стенок выработок.
С увеличением площади сечения выработки депрессия местного сопротивления будет снижаться вследствие уменьшения скорости согласно формуле
h=ξγQ2/2gS2
При взаимном влиянии двух местных сопротивлений основные мероприятия по снижению сопротивления следует проводить во втором из них (по направлению движения).
СПИСОК ЛИТЕРАТУРЫ
1. Кирин Б .Ф ., Ушаков К .З . Рудничная и промышленная аэрология : Учеб .
для вузов . – М .: Недра , 1983. – 256 с .
2. Ушаков К .З ., Бурчаков А .С ., Пучков Л .А ., Медведев И .И . Аэрология горных предприятий : Учеб . для вузов . – М .: Недра , 1987. – 421 с .
3. Рудничная вентиляция : Справ . /Под ред . К .З . Ушакова . – М .: Недра , 1988.– 440 с .
4. Правила безопасности в угольных шахтах . – Самара : Самарск . дом печати ,1995. – 242 с .
5. Проходчик горных выработок : Справ . /Под ред . проф . А .И . Петрова – М .:Недра , 1991. – 646 c.
Дата добавления: 2015-02-23; просмотров: 5618;
