Процедура простого случайного отбора.

По сформированной основе выборки легко реализовать процедуру простого случайного отбора. Для этого требуется соблюдение равенства шансов попадания единиц отбора в выборочную совокупность. Выделяют: а) простой случайный бесповторный отбор и б) простой случайный повторный отбор.

Осуществляться каждая из разновидностей процедуры может различными способами. Опишем один из них. Пусть основа выборки содержит N единиц. Тогда, чтобы выбрать п единиц наблюдения в выборочную совокупность, напишем все номера от 1 до N на отдельныe карточки, тщательно их перемешаем и наугад вынем одну из них. Номер вытащенной карточки задает соответствующую единицу наблюдения, попавшую в выборочную совокупность. Затем карточка возвращается на место, они снова перемешиваются, наугад, вынимается новая карточка, и так далее продолжается п раз. Так реализуется процедура простого случайного повторного отбора. Если извлеченную карточку не возвращать назад, а откладывать в сторону, то тот же процесс приведет нас к простой случайно бесповторной выборке размером в п единиц наблюдения или, как еще говорят, объемом в n единиц.

Описанная процедура простого, случайного отбора становится чрезвычайно трудоемкой, если число N, задающее объем основы вы­борки, велико. Главная трудность состоит в том, что обеспечение равной вероятности попадания единицы наблюдения в выборочную совокупность требует очень тщательного перемешивания.

Чтобы устранить трудности, возникающие при исследовании больших генеральных совокупностей (а именно таких большинство в социологии), для реализацию простого случайного отбора пользуются так называемыми таблицами случайных чисел. Они содержат те или иные случайные цифры, полученные путем реализации некоторого физического случайного процесса, В литературе приводятся различные последовательности случайных -чисел объемом от нескольких десятков до миллиона цифр (табл. 14).

Продемонстрируем, как работать с таблицей случайных чисел, на гипотетическом примере, когда из совокупности заранее прону­мерованных 300 единиц необходимо выбрать 7 единиц наблюдения. Поскольку N= 300 — трехзначное число, а в табл. 14 даны пяти­значные числа, будем использовать только три последних цифры каждого числа.

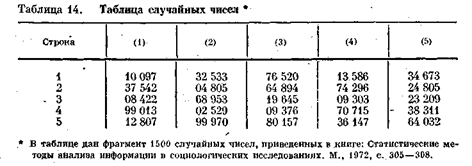
Начиная с первого числа, двигаясь по строке, получим первый номер 97. Числа более 300 пропускаем и, продолжая этот процесс далее, получим ряд чисел: 296, 209, 13, 157, 147, 32.

Это и есть номера единиц наблюдения, попавших в формируемую выборку.

При организации бесповторного отбора приходится пропускать и числа (если они попадаются), которые встречаются второй раз в этом ряду.

Начинать процесс выбора случайных чисел можно с любого места таблицы и вести его в любом направлении (по строкам, столбцам и т. п.) или выбирая только определенные столбцы. Если име­ющиеся под рукой таблицы достаточно длинны, то при решении очередной задачи выбора рекомендуется начинать с нового места таблицы.