Систематический отбор.

В социологических исследованиях иногда применяется несколько, упрощенный вариант простого случайного отбора, который носит название систематического. Основа выборки для него характеризуется теми же требованиями, что и для простого случайного отбора. Иными словами, основу выборки составляют раз­личные алфавитные списки, картотеки учреждений, домовые книги и т. п. При систематическом отборе выбор единиц наблюдения осу­ществляется через один и тот же интервал /г из исходного списка. Например, при А = 20 выбирается 3, 23, 43, 63 и т. д. единиц списка.

Таким образом, элементы выборочной, совокупности однозначно определяются при систематическом отборе номером первого элемен­та (тройки в нашем примере) и величиной интервала А.

В одной из схем систематического отбора в качестве первого элемента выбирается средний элемент списка или стоящий рядом с ним. Так, если список генеральной совокупности пронумерован от 1 до N, то номер первого элемента может быть определен по формулам (N+1)/2 если N—нечетное и N/2, если N- четное число.

Более распространен выбор первой единицы отбора случайным об­разом (например, по таблице случайных чисел).

Величина А зависит от характера поставленной проблемы, от разброса значений исследуемой характеристики генеральной сово­купности.

Если решен вопрос об объеме планируемой выборки, то число определяется, в зависимости от объема генеральной совокупности и объема выборки (и).

Если N — кратное числа n, то интервал определяется по формуле k=N/n. Если Nне кратно n, то реальный объем выборки n_p и планируемый объем n_пл .при различных способах вычисления числа А связаны следующими соотношениями:

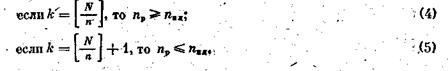
Здесь [ ] означает целую часть числа. Поясним сказанное на примере: пусть N=19 и n=5, чему равно k? Тогда k равно либо 3, либо 4.

При k= 3 в выборку попадает больше пяти элементов — в данном случае 6 пли 7. При k= 4 в выборку попадут пять или четыре элемента.

Расчет характеристик систематической выборки. В связи с тем что систематическая выборка определяется как разновидность про­стого случайного отбора, ее характеристики рассчитываются с по­мощью соответствующих формул табл. 16.

В примере с подписчиками газет и журналов (см. табл. 15) в систематическую выборку объемом 5 единиц попали номера респондентов 10, 20, 30, 40, 50, для которых соответствующее число вы­писываемых газет равно 3, 5, 5, .3, 2. Среднее по выборке равно 3,6, а дисперсия — 1,4.4 (s= 1,2).

Таким образом, с вероятностью 0,95 можно утверждать, что до­верительный интервал для генеральной средней имеет следующие границы: (3,6± 1,96-0,54) = (3,6 ±1,05) ==(2,55; 4,65).

Возможности и ограничения систематической выборки. Система­тическая выборка является экономным и удобным способом форми­рования выборочной совокупности. Однако при ее применении в социологических исследованиях необходимо следить за тем, чтобы список, используемый в качестве основы выборки, не обладал порядком, отражающим периодичность в значениях изучаемой харак­теристики. Проиллюстрируем это положение. При составлении основы выборки для опроса рабочих в одном из цехов завода выбранный интервал может совпасть с числом рабочих в бригаде, в списке который первым окажется бригадир. При систематическом отборе повышаются шансы попадания в выборку только одних бригадиров. При такой реализации выборки повышается вероятность получения значительных систематических ошибок.

Предварительное расположение элементов генеральной совокуп­ности по убыванию или возрастанию исследуемой характеристики дозволит избавиться отэтой опасности. Так, если в рассмотренном примере основа выборки организуется на базе платежной ведомости, в которой лица расположены в порядке возрастания их заработной платы, то опасность попадания только на одних бригадиров исклю­чается.

Систематическая выборка из-за простоты реализации получила широкое применение в социологических исследованиях.