Ряды распределения.

Результат группировки единиц наблюдения по какому-либо признаку называется статистическим рядом. Обозначим группировочный признак х. Пусть это будет уровень образова­ния каждого человека в данном списке лиц. Получим неупорядочен­ный ряд результатов отдельных наблюдений: 10, 5, 7, 8, 10, 10 10 (классы). Если отдельные наблюдения расположить в порядке воз­растания указанных выше значений признака, то получим вариаци­онный ряд: 5, 7, 8, 10, 10, 10, 10.

По вариационному ряду количественного признака можно под­считать, как часто каждое значение этого признака встречается в совокупности. В результате получим частотное распределение для данного признака. Иногда его называют эмпирическим или стати­стическим распределением. Для вышеприведенного примера частотное распределение выглядит так:

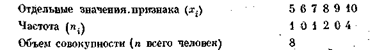
Условимся каждое, отдельное значение признака х обозначать х₁, х₂,… , x_k (в данном примере это 5, 7, 8, 9 и 10 классов).

Абсолютное число, показывающее, сколько раз встречается то или иное значение признака х, называется частотой и обозначается соответственно n₁, n₂, ..., n_k.

Относительной частотой называется доля значений признака в общем числе наблюдений и обозначается m₁, .,., m_k.

Например, для приведенного частотного ряда частота наиболь­шего значения признака (10 классов) равна 4, а относительная частота m₅ = 4/8 = 0,5. Относительную частоту обычно выражают в процентах (m_k = 50%).

Сгруппированные данные. Как правило, для последующей статистической обработки или более наглядного представления данных отдельные значения признаков объединяются в группы (интервалы). В этом случае частоты соотносят уже не с каждым отдельным зна­чением признака, как это делалось в предыдущем примере, а с ря­дом значений, попадающих в определенный интервал.

Например, распределение уровня образования в вышеприведенном примере может быть представлено в виде интервального ряда следующим образом:

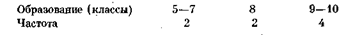
Частотное распределение с не сгруппированными значениями иногда называют дискретным рядом распределения.

При построении интервальных рядов большое значение имеет выбор типа, количества и размеров интервалов. Общее требование к этому выбору состоит в том, что группировка должна наиболее полно выявлять существенные свойства рядов распределения.

Существующие формальные правила выбора оптимальной вели­чины интервалов редко оказываются полезными при работе с социо­логическими данными¹³. Как правило, приходится делать выбор между двумя крайностями: слишком крупные интервалы для дан­ного объема выборки скрадывают многие нюансы в описании явле­ния, а слишком дробные ведут к статистически незначимым малым частотам внутри интервала.

Интервальные ряды распределения могут строиться с равными и неравными интервалами. Неравные интервалы применяются при неравномерном распределении частот значений группировочного признака — для выделения качественно отличных типов явлений. Например, выбор интервалов при группировке данных распределения совокупности опрошенных по возрасту можно основываться на этапах жизненного цикла. При группировке семей по признаку «число книг в семье», опираясь на информацию ранее проведенных исследований о том, что чаще всего встречаются библиотеки с чис­лом книг по 500 и реже — библиотеки, насчитывающие 10000 книг, целесообразно установить неравные интервалы группировки, напри­мер такие: 1—50, 51—100, 101—200, 201—300, 301—500, 501—700, 701-1000, 1001-2000, 2001—5000, 5001-10000.

Если у исследователя нет предварительной информации, о харак­тере распределения по тому или иному признаку, то следует зада­вать равные интервалы. Равные интервалы также наиболее удобны при использовании методов математической статистики. Опыт пока­зывает, что по каждому из признаков не следует брать более 20 группировочных интервалов.

При образовании интервалов необходимо точно обозначить коли­чественные границы группы, избегая таких обозначений границ интервалов, при которых отдельные единицы совокупности могут быть отнесены в две соседние группы. Поэтому, как правило, необ­ходимы дополнительные указания о том, считать ли граничные значения интервалов «включительно» или «исключительно».

Довольно часто социологу приходится сталкиваться с ситуацией, когда необходимо провести перегруппировку материала, задав дру­гие интервалы, но нет возможности при этом обратиться к перво­начальным статистическим данным.

При расщеплении интервала на несколько частей приходится вводить априорное предположение о частотном распределении внут­ри интервала, поскольку истинное распределение неизвестно. Самым простым является предположение о равномерности частотного рас­пределения по отдельным значениям признака. Другие формы распределения требуют достаточно громоздких вычислений¹⁴.