Свободные (затухающие) колебания в последовательном RLC-контуре.
Цель работы:наблюдение затухающих колебаний на экране осциллографа и экспериментальное определение характеристик колебаний и параметров контура.
Приборы и принадлежности:генератор прямоугольных импульсов (в блоке ГН1), цифровой осциллограф PicoScope 2203, стенд С-ЭМ01, соединительные провода.
Краткие теоретические сведения:
Уравнение свободных колебаний в последовательном RLC –контуре (рис.1) может быть получено из второго правила Кирхгофа:
Uc +UR = es,
где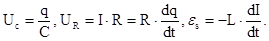 
Окончательно уравнение принимает вид
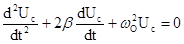, (1)
где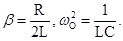 
Решением уравнения (1) при малом затухании (b2<<wо2) является функция, описываемая уравнением
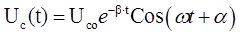, (2)
где w-частота затухающих колебаний, b-коэффициент затухания,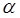 
- начальная фаза, 
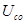-максимальное напряжение на конденсаторе
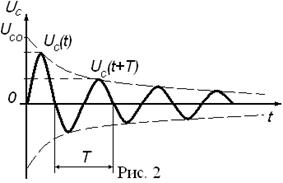Период затухающих колебаний Т при малом затухании можно приближенно считать равным периоду незатухающих колебаний Т0
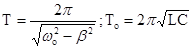. (3)
Важной характеристикой затухающих колебаний является логарифмический декремент затухания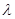 
, характеризующий уменьшение амплитуды колебаний за один период
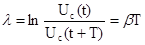, (4)
где Uc(t)-амплитуда затухающих колебаний в момент времени t; Uc(t+T)- амплитуда затухающих колебаний через период в момент времени t+T.
При малом затухании (w » wо) для l можно использовать формулу
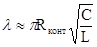, (5)
где Rконт- общее активное сопротивление контура.
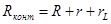, (6)
где R – внешнее сопротивление, r – внутренне сопротивление источника тока,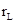 
- активное сопротивление катушки.
Критическое сопротивление контура, при котором колебательный процесс переходит в апериодический, может быть найдено из условия bкр=wо.
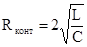. (7)
Добротность контура Q равна
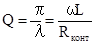. (8)
Дата добавления: 2015-02-19; просмотров: 1598;