Изучение сложениЯ колебаний

Цель:экспериментально исследовать явления, происходящие при сложении колебаний.

Приборы и принадлежности: блок генератора напряжений ГН1, блок амперметра-вольтметра АВ1, функциональный генератор АНР-1002, стенд с объектами исследования С3-ЭМ01, цифровой осциллограф PicoScope 2203, соединительные провода.

Краткие теоретические сведения

1. Сложение сонаправленных колебаний

Рассмотрим два гармонических колебания, совершаемые в одном направлении.

.

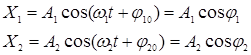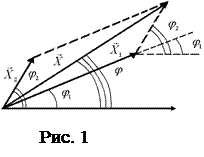
Для вычисления амплитуды и фазы результирующего колебания применяется метод векторных диаграмм. Сущность метода заключается в том, что каждому колебанию сопоставляется вектор, модуль которого пропорционален амплитуде колебания, а направление будет отличаться от некоторого, наперед заданного, на угол равный фазе колебания. Данное правило проиллюстрировано на рис. 1. Колебаниям Х₁ и Х₂ соответствуют вектора 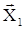и . 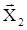Результирующему колебанию соответствует вектор 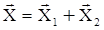. Как видно из рисунка амплитуда результирующего колебания может быть легко найдена по теореме косинусов

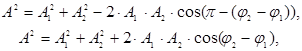(1)

а начальная фаза определяется соотношением

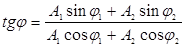(2)

Картина колебаний является неизменной, если их амплитуда не изменяется со временем. Из (1) видно, что это возможно только в случае, если частоты складываемых колебаний w₁ и w₂ одинаковы.

2. Биения

Биениями называются колебания, получающиеся при сложении двух сонаправленных колебаний с близкими частотами, такими, что Dw = w₂-w₁<<w₁, w₂. В этом случае амплитуда результирующих колебаний является медленно меняющейся периодической функцией времени. Типичная картина биений приведена на рис. 2.

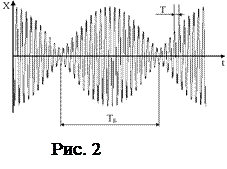Для простоты рассмотрим сложение двух колебаний с равными амплитудами А₁ = А₂ = А₀ и одинаковыми начальными фазами 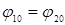. В соответствии с (1) амплитуда результирующего колебания (рекомендуется самостоятельно проделать преобразования)

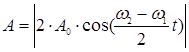. (3)

В последнем выражении поставлен модуль, так как амплитуда по своему смыслу не может быть отрицательной. Из (3) следует, что амплитуда колебаний будет меняться от минимального значения до максимального (в общем случае от | А₁ - А₂| до А₁ + А₂) с частотой, называемой частотой биений.

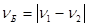(4)

3. Сложение взаимно перпендикулярных колебаний

Рассмотрим движение точки, участвующей в двух взаимно перпендикулярных колебаниях, происходящих вдоль осей X и Y :

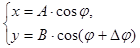. (5)

где 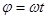- фаза колебаний

Перепишем уравнения в другом виде

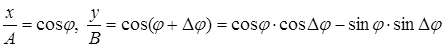. (6)

Заменив во втором уравнении cos j на 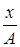, а sinj на 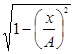, получим уравнение

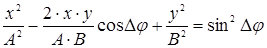. (7)

В случае, когда складываются колебания с одинаковой частотой и разность их фаз остается постоянной, последнее уравнение описывает эллипс, оси которого произвольно ориентированы относительно осей X и Y. В общем случае, когда частоты складываемых колебаний различны, траектории колеблющейся точки представляют собой сложные линии. Если частоты колебаний вдоль взаимно перпендикулярных осей соотносятся как целые числа

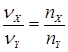, (8)

то линии оказываются замкнутыми и называются фигурами Лиссажу (числа n_X, n_Y можно определить, посчитав количество пересечений линии, образующей фигуру Лиссажу, с осями координат X и Y, причем, если ось проходит через точку пересечения ветвей фигуры Лиссажу, то эту точку считают дважды). Вид этих кривых зависит от соотношения частот, амплитуд и разности фаз складываемых колебаний, поэтому анализ фигур Лиссажу широко используется при исследовании колебаний.