Краткие теоретические сведения. Последовательный колебательный контур состоит из конденсатора ёмкостью C, соленоида индуктивностью L
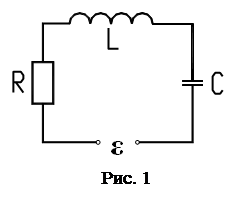
Последовательный колебательный контур состоит из конденсатора ёмкостью C, соленоида индуктивностью L, омического сопротивления R и источника переменной ЭДС e, включенных последовательно (рис. 1).
По закону Ома для неоднородного участка цепи сила тока:
I=(e + es – Dj)/R, (1)
где e - ЭДС источника переменного напряжения, которая изменяется по синусоидальному закону e=e0sin(Wt), es - ЭДС самоиндукции, возникающая в соленоиде, Dj - разность потенциалов на обкладках конденсатора, которую в дальнейшем будем обозначать через U.
Преобразуя (1), составим дифференциальное уравнение, описывающее колебательный процесс в рассматриваемом контуре
IR = e – LdI/dt – U, (2)
где es = – LdI/dt, Dj = U.
Силу тока в цепи I и напряжение на конденсаторе U можно связать, рассматривая процесс изменения заряда конденсатора:
I = dq/dt, U = q/C, I = CdU/dt (3)
Подставив (3) в (2), получим:
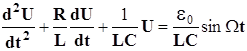 (4)
(4)
Введём обозначения: R/2L=b, 1/CL=w02и e0/CL=E0 (w0 - частота собственных колебаний контура, b - коэффициент затухания, W - частота внешней ЭДС). После их подстановки в (4) имеем неоднородное дифференциальное уравнение вынужденных колебаний:
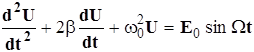 (5)
(5)
Решением его является сумма частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения, которым в установившемся режиме колебаний можно пренебречь. Частное решение неоднородного уравнения (5) имеет вид:
U=U0(W)sin(Wt+j), (6)
где амплитуда напряжения на конденсаторе U0может быть найдена подстановкой (6) в (5). Параметр j, представляющий собой сдвиг фаз колебаний напряжения на конденсаторе по отношению к колебаниям вынуждающей ЭДС, в лабораторной работе не определяется.
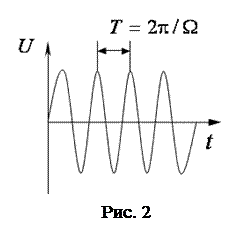 График вынужденных колебаний напряжения на конденсаторе (уравнение (6)) представлен на рис. 2. Вынужденные колебания происходят с частотой вынуждающей ЭДС Ω.
График вынужденных колебаний напряжения на конденсаторе (уравнение (6)) представлен на рис. 2. Вынужденные колебания происходят с частотой вынуждающей ЭДС Ω.
При приближении частоты внешнего вынуждающего воздействия Ω к собственной частоте колебаний ω0 в контуре резко возрастает амплитуда колебаний напряжения на конденсаторе – происходит явление резонанса. В работе исследуется зависимость амплитуды колебаний напряжения на конденсаторе U0от Ω при разных сопротивления контура R.
Амплитуда вынужденных колебаний:
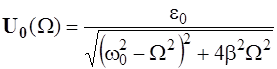 (7)
(7)
Из формулы (7) видно, что величина U0зависит прямо пропорционально от амплитуды вынуждающей ЭДС ε0и сложным образом от параметров колебательного контура w0и b. Исследование зависимости U0(W) показывает:
1) при W ® 0 напряжение на конденсаторе U0 ® e0;
2) функция U0(W) обладает максимумом при частоте генератора:
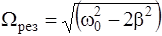 (8);
(8);
 3) напряжение на конденсаторе U0стремится к нулю при W ® ∞.
3) напряжение на конденсаторе U0стремится к нулю при W ® ∞.
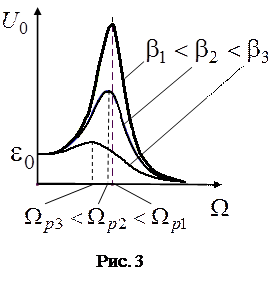
Графики зависимости U0(W) для различных коэффициентов затухания b приведены на рис. 3. Данные графики отражают явление резонанса напряжений. Частота вынуждающей ЭДС, при которой U0=U0max, называется резонансной. Она зависит от параметров колебательного контура (формула (8)).
Следует отметить, что резонанс для силы тока наблюдается при частоте w0, не зависящей от b.
Для колебательного контура вводится понятие добротности:
Qi = Uoi max/eo (9)
или: 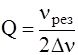 , (10)
, (10)
где 2Dn- ширина резонансной кривой при 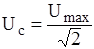 .
.
Дата добавления: 2015-02-19; просмотров: 945;
