Теоретическое введение. Коническими называются передачи, у которых ведущее и ведомое зубчатые колёса вращаются на пересекающихся осях под некоторым углом Σ

Коническими называются передачи, у которых ведущее и ведомое зубчатые колёса вращаются на пересекающихся осях под некоторым углом Σ. Наиболее распространены передачи с углом Σ = 90º. Каждое колесо имеет форму усечённого конуса, что отображено на рис. 3.1.

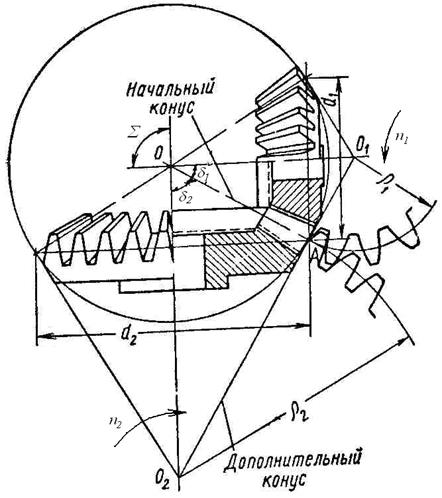
Рис. 3.1. Коническая зубчатая передача

Кинематической характеристикой конической зубчатой передачи, как и других видов передач, является передаточное отношение i = n₁/n₂. Передаточное число определяется как u = z₂ / z₁, где z₂ и z₁ – числа зубьев колеса и шестерни соответственно (z₁min > 17 cos δ₁), которые согласовываются со стандартным рядом по ГОСТ 2185-66.

Конические зубчатые колеса сложнее цилиндрических в изготовлении и монтаже. Для нарезания конических зубчатых колес требуются специальные станки и инструмент. Зубья конических колёс нарезают так же, как и цилиндрических – методом обкатки на специальных станках инструментом с прямобочным профилем (рис. 3.2). Профили зубьев очерчиваются по эвольвенте.

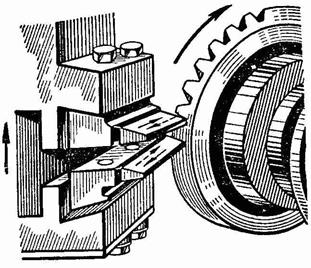
Рис. 3.2. Изготовление конических зубчатых колес

Геометрические параметры конического колеса монотонно уменьшаются по мере приближения к вершине конуса, поэтому различают внешние, средние и внутренние параметры зацепления. На рис. 3.3 изображен разрез конической шестерни. Параметрам внешних дополнительных конусов присваивают индекс е, внутренних – индекс i, средних – индекс m.

Для обозначения параметров по конусу вершин используют индекс а, по конусу впадин – f, по делительному конусу индекс отсутствует. В обозначении диаметра необходимо включать три индекса, указывающие на дополнительный конус (e, i, m), основной (а, f) и на ведущее (1) или ведомое (2) колесо. Например, d_fe1 – диаметр впадин шестерни по внешнему дополнительному конусу. Все поперечные сечения зуба геометрически подобны. Высота зуба и модуль тоже монотонно уменьшаются по мере приближения к вершине корпуса. Различают модули внешний m_е, средний m_m, внутренний m_i, а в произвольном заданном сечении m_x. Такими же индексами обозначают высоту зуба h в различных торцевых сечениях колеса.

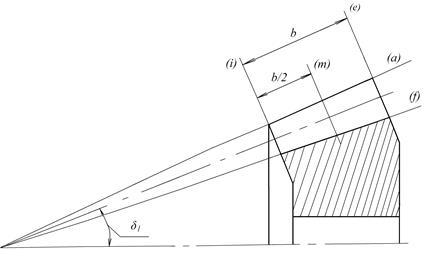
Рис. 3.3. Коническая шестерня

На практике за расчетное сечение принято среднее сечение зуба, которому соответствует модуль – m_m. Со стандартным рядом согласовывается внешний модуль m_е по ГОСТ 9653 – 60.

На рис. 3.4 представлено зацепление пары конических зубчатых колёс и геометрические параметры передачи.

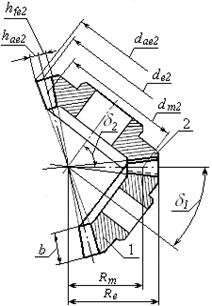
Рис. 3.4. Коническое зубчатое зацепление

Основные зависимости для определения геометрических параметров конических прямозубых передач при δ₁ + δ₂ = 90° в соответствии с ГОСТ 19624-74:

– угол делительного конуса колеса δ₂ = arctg u;

– внешний делительный диаметр d_e = m_ez;

– внешнее конусное расстояние R_e = 0,5 m_e ;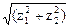

– среднее конусное расстояние R = R_е – 0,5b;

– средний окружной модуль m = m_e R/R_e;

– средний делительный диаметр d = mz;

– внешняя высота зуба h_e = 2,2 m_e;

– внешняя высота головки зуба h_ае = m_e;

– внешняя высота ножки зуба h_fe = 1,2 m_e;

– внешний диаметр вершин зубьев d_ae = d_e + 2 h_ae cos δ.

Для нормальной работы передачи вершины конусов конических зубчатых колёс должны совпадать с точкой пересечения их осей. Если при монтаже это условие нарушено и колёса оказались смещёнными в осевом направлении, в любом из торцевых сечений основные шаги становятся неровными и в зацеплении возникают дополнительные нагрузки. Осевые смещения изменяют также характер продольного контакта: теоретический линейный контакт фактически превращается в точечный и точка контакта лежит во внешнем или внутреннем торцевых сечениях в зависимости от направления осевых смещений, вследствие этого возникает концентрация нагрузки на краях зубьев.