Универсальное соотношение неопределенности Шредингера

Флуктуация в микромире чувствительна к квантовому воздействию, а в макромире к тепловому воздействию. На их границе могут происходить оба типа флуктуации. Австрийский физик-теоретик Эрвин Шредингер, в 1930,году установил универсальное соотношение неопределенности, которое показывает возможности проявления двух типов корреляции между флуктуациями физических характеристик объектов и их состояний. Универсальное соотношение неопределенности Шредингера(СНШ) описывается в следующем виде:

∆А²ּ∆В² ≥R 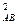/4,

где ∆А и ∆В – флуктуации величин А и В, R 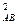/4 – мера корреляции этих флуктуаций, цифра «4» показывает, что претерпевают флуктуацию четыре величины. Величину R_АВ – можно представить в виде суммы двух корреляторов:

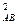R 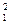=R +R ,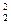

где R₁ – коррелятор между флуктуациями ∆А и ∆В в фазе, а R₂ – в противофазе. Таким образом, СНГ в микромире, а СНЭ в макромире являются частными случаями СНШ.

В качестве примера СНШ, может служить электромагнитная бегущая волна, в которой электрические и магнитные поля взаимно перпендикулярны. Мерой корреляции, в данном случае является векторное произведение векторов 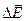и 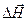. При φ=0, величина R₁= =∆Еּ∆Нּcosφ=1, корреляция между флуктуациями в фазе. При φ=90⁰ величина R₂=∆Еּ∆Н∙sinφ=1 - корреляция между флуктуациями в противофазе. При этом квадрат меры корреляций R 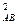определяется по формуле:

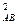R 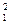=R +R 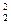, =(∆Еּ∆Нּcosφ)²+(∆Еּ∆Н∙sinφ)²=∆Е²ּ∆Н².

Последняя формула показывает, что мера корреляции R 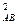не зависит от угла между векторам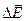и и .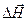

Таким образом, наличие корреляции между флуктуациями показывает целостность природы, как в микромире, так и в макромире. Введение таких корреляций и в других науках, в том числе и в гуманитарных науках, имеет значение для формирования целостного взгляда на культуру.

Тема 16. Синергетка – наука о самоорганизации