Работа процесса.
Используя уравнение политропы, выразим работу расширения (1.9) через начальные и конечные параметры процесса
lрасш = 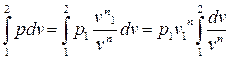 .
.
После интегрирования и некоторых преобразований получим:
lрасш = 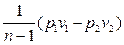 =
= 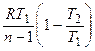 .
.
Заменив отношение температур отношением давлений, будем иметь:
lрасш= 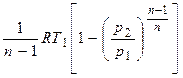 . (2.52)
. (2.52)
Проводя те же операции, что и при выводе lрасш получим уравнение для технической работы в виде
lтех = - 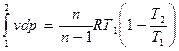
или
lтех = 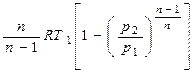 . (2.53)
. (2.53)
Сравнивая выражения (2.52) и (2.53), видим, что техническая работа в n раз больше работы расширения, т.е.
lтех = n lрасш.
Теплота процесса.
Теплоту политропного процесса выражают через теплоемкость, либо используют для этого выражение первого закона термодинамики:
q = cп (Т2 – Т1) = cv 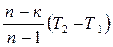 ,
, 
q = ∆u + lрасш = cv (Т2 – Т1) - 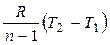 ,
,
q = 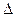 i + lmex = cp (T2 – T1) -
i + lmex = cp (T2 – T1) - 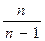 R (T2 – T1 ).
R (T2 – T1 ).
Дата добавления: 2015-02-16; просмотров: 877;
