Ступенчатому воздействию соответствует функция
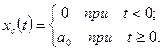
При анализе и расчете систем удобно использовать ступенчатое воздействие, у которого величина а0 = 1. Его называют единичным ступенчатым воздействием (единичным скачком) и обозначают 1(t). Математическое выражение, описывающее единичный скачок, имеет вид
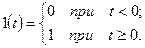
Ступенчатое воздействие чаще всего используют при испытаниях и расчетах систем стабилизации, так как эти воздействия наиболее близки к реальным входным (задающим и возмущающим) воздействиям систем стабилизации.
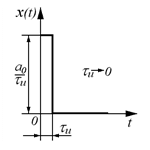
Импульсное воздействие представляет собой одиночный импульс прямоугольной формы (см. рис.), имеющий достаточно большую высоту и весьма малую продолжительность (по сравнению с инерционностью испытываемой системы). Очевидно, что площадь такого импульса всегда равна а0.
 При математическом анализе автоматических систем используют единичное импульсное воздействие, которое описывается так называемой дельта – функцией
При математическом анализе автоматических систем используют единичное импульсное воздействие, которое описывается так называемой дельта – функцией
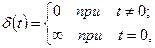
причем
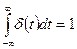
Согласно этим выражениям, дельта – функцию можно рассматривать как импульс, имеющий бесконечно большую высоту, бесконечно малую длительность и единичную площадь. Дельта – функцию можно определить также как производную единичного скачка:
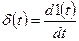 .
.
В качестве стандартного гармонического воздействия используют обычно сигнал синусоидальной формы, описываемый функцией
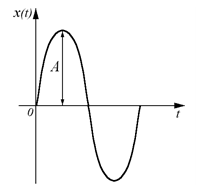
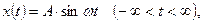
где А – амплитуда сигнала;
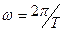 - круговая частота, рад/с;
- круговая частота, рад/с;
Т – период сигнала, с.
Гармонические воздействия широко используются при исследовании точности и устойчивости как стабилизирующих, так следящих и программных автоматических систем. Это объясняется двумя обстоятельствами: во – первых, реальные возмущения часто имеют периодический характер и поэтому могут быть представлены в виде суммы гармонических составляющих; во – вторых, математический аппарат анализа автоматических систем хорошо разработан именно для случая гармонических воздействий.
Для следящих и программных систем типовым является линейное воздействие (см. рис.)
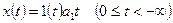
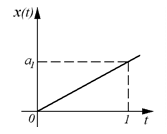 .
.
Коэффициент а1 характеризует скорость нарастания воздействия x(t).
Дата добавления: 2015-02-16; просмотров: 1218;
