Краткие теоретические сведения. Основные понятия и определения

Основные понятия и определения

Открытое Фарадеем в 1831 году явление электромагнитной индукции лежит в основе закона электромагнитной индукции, являющимся одним из фундаментальных законов теории электромагнитных явлений. Суть его заключается в том, что при любом изменении магнитного поля, пронизывающего какой-либо контур, в нем возникает электродвижущая сила. Поскольку возникновение ЭДС связано с появлением электрического поля, можно сделать вывод о том, что оба эти поля − магнитное и электрическое − являются двумя сторонами единого электромагнитного поля.

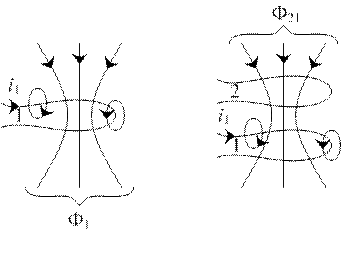
Рассмотрим контур 1, по которому течет ток i₁ (рис. 4.1,а). Магнитный поток Ф₁ , сцепленный с контуром, определяется током i₁. Этот поток называется потоком самоиндукции.

а) б)

Рис. 4.1. Индуктивная связь между контурами:

а) первый контур с током; б) второй контур

в магнитном поле первого

Контур может представлять собой катушку с числом витков w₁. Поток самоиндукции сцепляется со всеми витками. Поэтому вводят понятие потокосцепления самоиндукции Ψ₁, которое определяется как произведение магнитного потока самоиндукции Ф₁ на число витков w₁:

Ψ₁ = w₁ Ф₁ .

Связь потокосцепления самоиндукции Ψ₁ с вызвавшим его током i₁ определяется выражением

Ψ₁ =L₁i₁ , (4.1)

где L₁ − собственная индуктивность или просто индуктивность контура, зависящая от его геометрических размеров, числа витков и свойств среды, в которой он расположен.

Если по каким-то причинам происходит изменение потокосцепления Ψ₁ (за счет изменения тока, геометрии контура, числа витков или свойств среды), то в соответствии с законом электромагнитной индукции в витках катушки возникает ЭДС самоиндукции e_L1, величина которой пропорциональна скорости изменения потокосцепления:

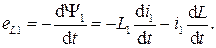
Для линейных цепей, рассматривающихся в настоящем разделе, L₁ =const, и ЭДС самоиндукции определяется лишь скоростью изменения тока:

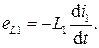
Знак минус означает, что в системе контуров с электрическими токами существует тенденция к сохранению неизменными магнитных потоков, сцепленных с ними. При всякой попытке изменить эти потоки в контурах возникают электродвижущие силы, вызывающие токи, стремящиеся воспрепятствовать этому изменению.

ЭДС самоиндукции соответствует равное по величине, но противоположное по направлению напряжение самоиндукции u_L1 :

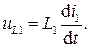(4.2)

Расположим рядом с первым контур 2 (рис. 4.1,б). Силовые линии магнитного поля первого контура сцепляются со вторым. При этом не весь магнитный поток Ф₁ пронизывает второй контур. Часть потока первого контура, сцепляющаяся со вторым контуром, называется потоком взаимной индукции и обозначается Ф₂₁. Соответственно потокосцепление взаимной индукции Ψ₂₁ со вторым контуром пропорционально току первого контура:

Ψ₂₁=w₂ Ф₂₁ = Mi₁, (4.3)

где w₂ − число витков второго контура; M − взаимная индуктивность между контурами, зависящая от геометрических размеров контуров, их взаимного расположения, числа витков и свойств среды, в которой они находятся.

Разность между потоками самоиндукции Ф₁ и взаимоиндукции Ф₂₁ называется потоком рассеяния и обозначается Ф_S1.

При изменении потокосцепления взаимной индукции Ψ₂₁ во втором контуре в соответствии с законом электромагнитной индукции возникает ЭДС взаимной индукции e₂₁, равная

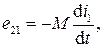
и соответствующее этой ЭДС напряжение взаимной индукции u₂₁:

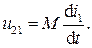(4.4)

Аналогичные рассуждения справедливы и в случае протекания тока i₂ во втором контуре.

Току i₂ второго контура соответствует поток Ф₂ и потокосцепление самоиндукции Ψ₂ (на рис.4.1 не обозначены):

Ψ₂ = w₂ Ф₂ = L₂i₂, (4.5)

где L₂ − индуктивность второго контура. Соответственно, во втором контуре возникает напряжение самоиндукции u_L2 :

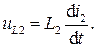(4.6)

Часть Ф₁₂ потока Ф₂ второго контура (поток взаимной индукции) сцепляется с первым контуром. Тогда потокосцепление первого контура от потока Ф₁₂ равно:

Ψ₁₂= w₁ Ф₁₂= Mi₂. (4.7)

При этом в первом контуре возникает напряжение взаимной индукции u₁₂

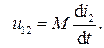(4.8)

Таким образом, поток каждого контура складывается из собственного потока самоиндукции и потока взаимной индукции, созданного током в другом контуре. Если в электрической цепи имеется несколько пар индуктивно-связанных контуров, то взаимной индуктивности М также присваиваются два индекса, например, М₁₂ и М₁₃.

Двойные индексы в обозначениях величин взаимной индукции обозначают следующее: первый индекс указывает, с какой цепью сцепляется поток взаимной индукции, а второй указывает на ток, создающий поток взаимной индукции. В линейных цепях для индуктивно-связанных катушек справедливо равенство

М₁₂= М₂₁= М.

Степень магнитной связи контуров (или индуктивных катушек) принято оценивать коэффициентом связи k, который характеризует долю потокосцеплений взаимной индукции в потоках каждой катушки и с учетом выражений (4.1), (4.3), (4.5), (4.7) равен :

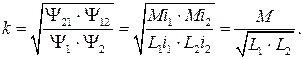
Магнитный поток самоиндукции катушки и поток взаимоиндукции от индуктивно связанной с ней другой катушки могут совпадать по направлению, а могут быть направлены навстречу друг другу. В первом случае говорят, что контуры включены согласно, а во втором - встречно. При согласном включении в каждом контуре напряжения само- и взаимоиндукции имеют одинаковое направление, при встречном − противоположное. Следует заметить, что направление магнитного потока, создаваемого током катушки, зависит не только от направления тока, но и от того, как намотаны витки: по или против часовой стрелки. Поэтому при рассмотрении схем с индуктивно-связанными контурами возникает двойственность при определении направления напряжений взаимоиндукции.

Для того, чтобы однозначно определять способ включения катушек, вводят понятие одноименных зажимов, которые обозначаются звездочкой. Если на электрической схеме токи в индуктивно-связанных катушках ориентированы относительно звездочек одинаково, то считают, что катушки включены согласно. В противном случае − встречно. Соответственно, и напряжения само- и взаимоиндукции в согласно включенных катушках ориентированы относительно одноименных зажимов одинаково. Для иллюстрации на рис.4.2 показаны направления токов и напряжений в согласно (а) и встречно (б) включенных катушках.

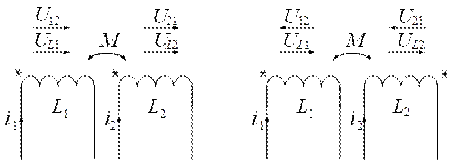
а) б)

Рис. 4.2. Напряжения само- и взаимоиндукции

в индуктивно-связанных катушках:

а) согласное включение; б) встречное включение

Направление падения напряжения самоиндукции, например, u_L1 совпадает с направлением тока i₁ в катушке. Падение напряжения взаимоиндукции u₁₂ в первой катушке направлено относительно одноименного зажима так же, как направлен ток i₂ относительно одноименного зажима второй катушки. Аналогично определяются направления остальных падений напряжения на рис. 4.2.

Очевидно, что общее падение напряжения на каждой катушке равно алгебраической сумме падений напряжения само- и взаимоиндукции.

В случае гармонических токов комплексы действующих значений напряжений само- и взаимоиндукции, например, для катушек рис. 4.2,а имеют вид:

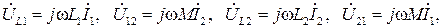(4.9)

где ω − угловая частоты гармонического тока; 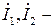комплексы действующих значений токов в катушках.