При наличии взаимной индукции

Рассмотрим порядок расчета цепей со взаимной индукцией на примере последовательного соединения индуктивно-связанных катушек.

Расчетная схема цепи приведена на рис. 4.3. Звездочка в скобках означает расположение одноименного зажима второй катушки при встречном включении.

Поскольку катушки индуктивности 1 и 2 как устройства намотаны проводом с конечным активным сопротивлением, то они на схеме представлены в виде последовательно соединенных активного сопротивления и индуктивности. На расчетной схеме показаны положительные направления тока 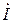, входного напряжения 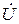и падений напряжения на катушках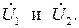

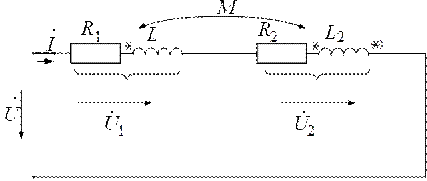
Рис. 4.3. Расчетная схема цепи с последовательным соединением катушек

Составим уравнения ЗНК для контура цепи, обойдя его по часовой стрелке. С учетом направлений падений напряжений на индуктивных элементах в соответствии с рис. 4.2 и соотношениями (4.9) получим:

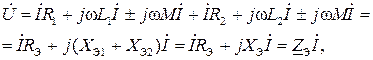(4.10)

где R_Э= R₁+ R₂; X_Э1=ω (L₁ ± M), X_Э2=ω (L₂ ± M) − эквивалентные реактивные сопротивления индуктивностей; X_Э=ω(L₁+L₂±2M) − реактивное сопротивление всей цепи; 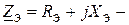комплекс входного сопротивления цепи.

Знак плюс в (4.10) относится к согласному включению, минус − к встречному.

Из (4.10) находим ток в цепи

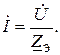
Как видно из полученных выражений, при согласном включении эквивалентное индуктивное сопротивление катушек больше, чем при встречном. Данный факт дает простой способ маркировки одноименных зажимов катушек.

Комплексное входное сопротивление 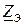можно выразить через комплексные сопротивления катушек следующим образом:

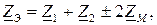
где 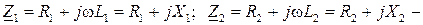комплексные сопротивления катушек без учета индуктивной связи; 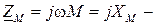комплексное сопротивление взаимной индукции.

Полезно напомнить, что при измеренных входном напряжении U, токе I в цепи и измеренной активной мощности P входное сопротивление полностью определено следующими соотношениями:

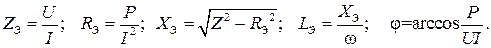(4.11)

На рис. 4.4 построена векторная диаграмма для согласного включения катушек.

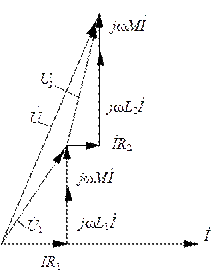
Рис. 4.4. Векторная диаграмма для последовательного

согласного включения катушек

Построение диаграммы начинается с изображения вектора тока 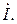Затем последовательно изображаются векторы падений напряжения на активном и индуктивных сопротивлениях катушек с одновременным векторным суммированием в соответствии с уравнением (4.10). Вектор 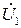соответствует падению напряжения на первой катушке, которое равно сумме падений напряжения на активном сопротивлении R₁ и индуктивных сопротивлениях само- и взаимоиндукции. Вектор 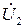соответствует падению напряжения на второй катушке. Сумма векторов 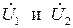представляет собой вектор 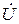входного напряжения.

Для встречного включения катушек студентам предлагается построить векторную диаграмму самостоятельно.