Схемы соединения трехфазных цепей

Самым простым способом соединения генератора с нагрузкой является соединение каждой фазной обмотки и соответствующей нагрузки с помощью двух проводов. В этом случае для трехфазной цепи понадобится шесть проводов. Количество проводов можно уменьшить, если использовать связывание трехфазной цепи. Основными способами соединения (связывания) фаз являются соединения звездой и треугольником, которые используются как для соединения фаз генераторов, так и для соединения фаз нагрузки.

Схема соединения фаз генератора и приемника звездой приведена на рис. 3.2.

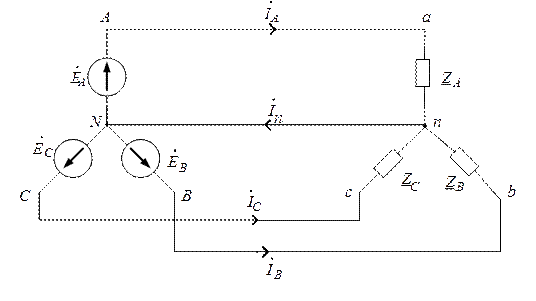
Рис. 3.2. Соединение трехфазной цепи по схеме "звезда-звезда"

с нулевым проводом

В данной схеме начала фазных обмоток генератора соединяются в нейтральную точку N генератора. Провод, соединяющий нейтральные точки N генератора и n нагрузки, называют нейтральным проводом, а провода, идущие от концов фаз (A,B,C) генератора к нагрузке (a,b,c), − линейными проводами. Очевидно, что нулевой провод и линейные провода обладают конечным сопротивлением. Поскольку сопротивления линейных проводов одинаковые, то для упрощения рассмотрения соотношений между напряжениями и токами в трехфазных системах ими можно пренебречь. Но при этом сохраняются обозначения соответствующих узлов генератора и нагрузки (например, A и a). Сопротивление нулевого провода также примем равным нулю, сохранив обозначения нейтральных точек N генератора и n нагрузки. Влияние сопротивления нулевого провода на работу трехфазной цепи будет рассмотрено ниже.

За положительное направление токов 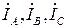в линейных проводах принимают направление от источника к приемнику. Если сопротивления нагрузки одинаковые (симметричная нагрузка), то линейные токи одинаковы по величине, разность фаз между ними равна 120 град., а их сумма и ток 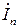в нулевом проводе в соответствии с ЗТК равны нулю. В этом случае необходимость в нулевом проводе отпадает, и энергию от генератора приемнику можно передавать с помощью только трех проводов. В экономии меди на проводах, соединяющих генератор и нагрузку, и заключается одно из преимуществ связывания трехфазной системы.

Схема соединения фаз генератора и приемника треугольником приведена на рис. 3.3.

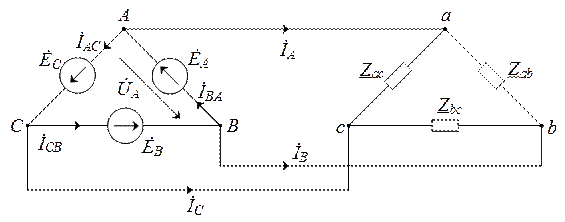
Рис. 3.3. Соединение трехфазной цепи

по схеме "треугольник-треугольник"

В данной схеме конец каждой фазной обмотки генератора соединяется с началом обмотки следующей фазы. Поскольку в симметричной системе сумма фазных ЭДС равна нулю, то в образованном фазными обмотками контуре суммарная ЭДС в соответствии с (3.1) равна нулю, и в режиме холостого хода (при отсутствии токов 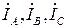нагрузки) токи в обмотках генератора 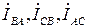равны нулю. Как видно из схемы рис. 3.3, данный способ соединения генератора с нагрузкой требует только три провода.

Следует заметить, что способы соединения фаз генератора и нагрузки независимы друг от друга, если не предусматривается нулевой провод. Возможны соединения по схемам: "звезда-треугольник", "треугольник-звезда". Чаще всего генератор соединяют звездой. Это обусловлено тем, что в реальных конструкциях генераторов в случае различия в величине фазных напряжений, обусловленного, например, несимметрией магнитной цепи и возможными технологическими погрешностями, при соединении фазных обмоток генератора треугольником даже при холостом ходе возникают уравнительные токи, что может привести к дополнительным потерям и снижению надежности системы. При соединении обмоток по схеме "звезда" уравнительных токов не возникает ввиду отсутствия контура для их замыкания.

Напряжения на зажимах отдельных фаз генератора и нагрузки называют фазными напряжениями, напряжения между линейными проводами − линейными напряжениями. Токи в фазах генератора и нагрузки называют фазными токами, токи в линейных проводах − линейными токами. Фазные напряжения и токи обозначаются с индексом "ф", линейные − с индексом "л".

Как следует из рис. 3.2 и 3.3, при соединении звездой фазные токи равны линейным, а при соединении треугольником фазные напряжения равны линейным:

− соединение звездой: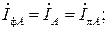

− соединение треугольником: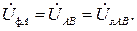

Аналогичные соотношения справедливы и для других фаз.

Для установления соотношений между фазными и линейными напряжениями при соединении по схеме "звезда" обратимся к рис.3.4.

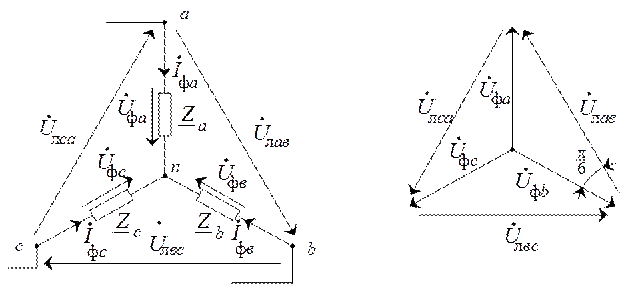
а) б)

Рис. 3.4. Соединение нагрузки по схеме звезда:

а) схема соединения; б) векторная диаграмма напряжений

Рассматривается случай симметричной нагрузки: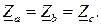

Фазные напряжения 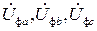образуют симметричную звезду векторов (рис. 3.4,б).

В соответствии с ЗНК связь между линейными и фазными напряжениями в соответствии с принятыми положительными направлениями на рис. 3.4,а определяется соотношениями:

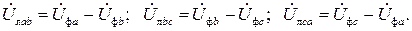
Из векторной диаграммы видно, что линейные напряжения 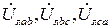образуют равносторонний треугольник. Угол между фазными и линейными напряжениями равен π/6. Тогда очевидно соотношение между действующими значениями фазных и линейных напряжений:

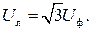(3.2)

Аналогичные соотношения имеют место между фазными и линейными токами для симметричной нагрузки при соединении фаз треугольником.

Рассмотрим рис. 3.5.

Поскольку векторы фазных напряжений 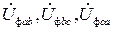образуют симметричную звезду, то при симметричной нагрузке 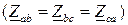фазные токи 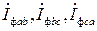также образуют симметричную звезду (рис. 3.5,б).

а) б)

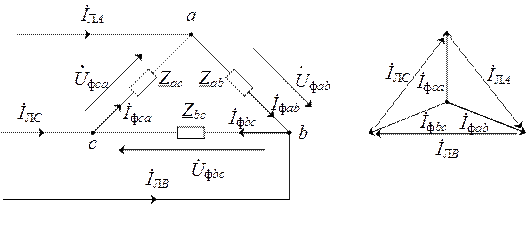
Рис. 3.5. Соединение нагрузки треугольником:

а) схема соединения; б) векторная диаграмма токов

В соответствии с ЗТК связь между линейными и фазными токами в соответствии с принятыми положительными направлениями на рис. 3.5,а определяется соотношениями:

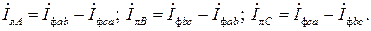(3.3)

Соотношения (3.3) справедливы не только для симметричной нагрузки. Если сложить линейные токи в (3.3), то получим важный вывод: в любой трехпроводной системе всегда сумма линейных токов равна нулю. Для соединения по схеме "звезда" данное утверждение очевидно.

Из векторной диаграммы рис. 3.5,б видно, что линейные токи 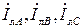образуют равносторонний треугольник. Угол между фазными и линейными токами равен π/6. Тогда очевидно соотношение между действующими значениями фазных и линейных токов:

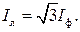(3.4)

В последующих разделах будут рассматриваться конкретные трехфазные схемы, где принадлежность к фазным и линейным напряжениям и токам будет очевидной. Поэтому для упрощения обозначений индексы "ф" и "л" указывать не будем.