Электронные таблицы

В повседневной деятельности инженера приходится решать ряд научных и производственных задач, в том числе и расчетов. Обычно результатами расчетов являются длинные колонки чисел. Обрабатывать большие массивы числовых данных, например результаты экспериментов, статистические данные и т.д., позволяют электронные таблицы. Наибольшее распространение получили таблицы Microsoft Excel.

Электронная таблица – это работающее в диалоговом режиме приложение, хранящее и обрабатывающее данные в прямоугольных таблицах.

Электронная таблица состоит из столбцов и строк. Заголовки столбцов обозначаются буквами или сочетаниями букв (A, B,C, AC), заголовки строк – числами (1, 2, 3 и т.д.). Ячейка – место пересечения столбца и строки. Адрес ячейки состоит из заголовка столбца и заголовка строки (А1, АС3). Ячейка, с которой производятся какие-либо действия, выделяется рамкой и называется активной.

Электронные таблицы, с которыми работает пользователь, называются рабочими листами. Документы электронных таблиц могут включать несколько рабочих листов и называются рабочими книгами.

В работе с электронными таблицами можно выделить три основных типа данных: число, текст, формула. В зависимости от решаемой задачи возникает необходимость применения различных форматов представления данных. В каждом конкретном случае можно выбрать наиболее подходящий формат.

В формулах используются ссылки на адреса ячеек. Существуют два основных типа ссылок: относительные и абсолютные.

Относительные ссылки в формулах используются для указания адреса ячейки, вычисляемого относительно ячейки, в которой находится формула. При перемещении или копировании формулы из активной ячейки относительные ссылки автоматически обновляются в зависимости от нового положения формулы. Относительные ссылки имеют следующий вид: А1, Р3. При копировании формулы, содержащей только относительные ссылки, из ячейки в ячейку, обозначения в формуле меняются.

Абсолютные ссылки в формулах используются для указания фиксированного адреса ячейки. При копировании или перемещении формулы, абсолютные ссылки не изменяются. В абсолютных ссылках перед неизменяемым значением адреса ячейки ставится знак доллара ($А$1).

Для производства вычислений используют формат формул. Формула должна начинаться со знака равенства и может включать числа, имена ячеек, функции и знаки математических операций. При вводе формулы в ячейке отображается результат вычислений. При изменении исходных данных, результат пересчитывается.

Таблицы Microsoft Excel предоставляют большую библиотеку встроенных функций следующих категорий:

– математические;

– статистические;

– финансовые;

– текстовые;

– логические;

– дата и время;

– ссылки и массивы;

– инженерные, и др.

Решение математической задачи в электронных таблицах – это способ получения результата за меньшее время, чем при обычном аналитическом решении, причем возможно решение задач следующих разделов математики: элементарная математика, высшая математика, теория вероятности и математическая статистика, численные методы. Excel предоставляет обширную библиотеку встроенных функций, которые можно найти на панели меню под названием «Мастер функции». После этого в диалоговом окне необходимо выбрать категорию, затем необходимую функцию (рисунок 3.1).

Рисунок 3.1 - Диалоговое окно выбора функции

Вычислить значение заданной функции можно непосредственно в ячейке. Ввод в ячейку аналитической заданной функции начинается со знака равно «=». После него вводится аналитическое выражение заданной функции, в котором переменные заменяются именами каких-либо ячеек, отличными от ячейки ввода, в которых находятся значения переменных. Нажатие на кнопку «Enter» завершает ввод функции. Автоматически в ячейке ввода появляется результат вычисления.

Вот один из примеров применения встроенных математических функций для решения задач горного производства (рисунок 3.2):

- вычислить относительную метанообильность шахты

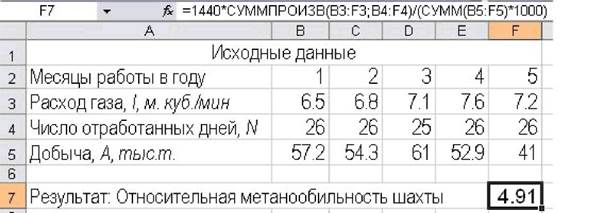
Рисунок 3.2 - Пример использования электронной таблицы при производственных расчетах

Электронные таблицы позволяют осуществлять сортировку данных, т.е. производить их упорядочение. Данные можно сортировать по возрастанию и убыванию. При помощи фильтров можно производить также поиск данных в соответствии с заданными условиями.

Электронные таблицы полезны и для научных целей. С их помощью можно строить компьютерные математические модели, проводить вычислительные эксперименты. Математической моделью называется информационная модель объекта или процесса, выраженная математическими средствами (формулами, уравнениями и т. п.).

Табличный процессор может применяться в качестве инструмента для математического моделирования.

Полученную математическую модель можно использовать для проведения вычислительного эксперимента. Вычислительный эксперимент – это математические расчеты с целью прогноза поведения какой-то системы, с целью выяснения вопроса о том, как изменение одних характеристик системы отражается на других.

При решении определенных задач в Excel нет необходимых встроенных функций. В так их случаях, при знании методов решения той или иной поставленной задачи, это можно сделать без проблем. К примеру, необходимо решить систему линейных алгебраических уравнений:

Встроенной функции для решения систем линейных алгебраических уравнений нет. По методу Крамера решение системы имеет вид

где Δ = det A, Δ_i – вспомогательный определитель, равный определителю матрицы системы, в которой i-й столбец заменен столбцом свободных членов.

Найти значения матриц можно при помощи встроенной функции «МОПРЕД».

Вычисление пределов и производных возможно, используя циклические ссылки. Расчеты по циклическим ссылкам поводятся через диалоговое окно, открываемое командами Сервис→Параметры→Вычисления (рисунок 3.3).

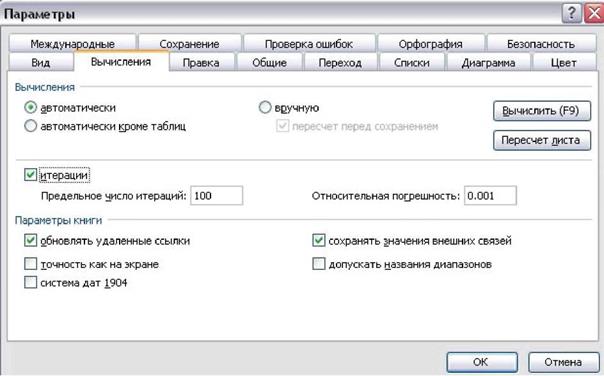
Рисунок 3.3 - Диалоговое окно (параметры) вычисления

Напротив параметра «итерации» ставится галочка, напротив параметра «Предельное число итераций» задается число повторений циклов, по умолчанию равное 100.

Например, вычислим первый замечательный предел

.

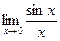Пример расчета предела показан на рисунке 3.4.

В ячейке А1 задаем формулу =А1+1. В ячейке А2 задаем формулу двустороннего приближения к предельной точке: =(-0,1)^А1.

Значение функции вычисляем по формуле =sin(А2)/А2 в ячейке А3.

Командами Сервис→Параметры→Вычисления открываем диалоговое окно, устанавливаем предельное число итераций 10. Нажимаем ОК. В ячейке А3 появляется результат.

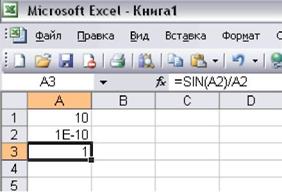
Рисунок 3.4 - Пример расчета предела с помощью электронной таблицы