ТЕКСТОВАЯ ИНФОРМАЦИЯ, ВЫЧИСЛЕНИЯ И ДЕЛОВАЯ ГРАФИКА

Преобразование энергии жидкости в механическую энергию на валу осуществляется в рабочем колесе за счет взаимодействия потока с лопастями рабочего колеса, представляющего собой вра­щающуюся решетку профилей.

Гидродинамические свойства потока в рабочем колесе, ха­рактеризуемые пропускной способностью турбины – Q, скоростью вращения – nи к. п. д. – η, определяются величиной и направлением скоростей в потоке жидкости. Скорости потока в свою очередь зависят: от формы и размеров элементов проточной части турбины и рабочего напора Н.

При исследовании движения жидкости в рабочем колесе это движение рассматривается как сложное, состоящее из двух движений: относительного и переносного. Относительное движение W жидкости фиксируется «наблюдателем», находящимся на рабочем колесе (движение ж., относительно системы координат прикрепленной к сосуду). Переносное движение Uопределяет движение самого рабочего колеса и его лопастей по отношению к неподвижным частям турбины.

В турбинах — это всегда вращение. Сумму

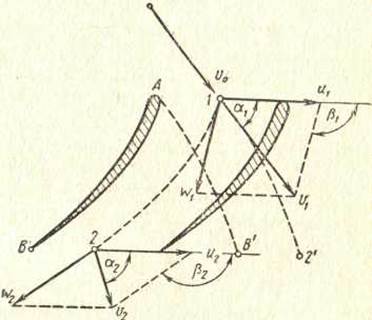
относительного и переносного движений называют абсолютным движением V, рисунок 4.4.

Рисунок 4.4 Скорости и траектория движения воды в межлопастном канале рабочего колеса РО турбины.

На рисунке 4.4 представлены следующие обозначения:

О — место ненарушенного (закрученного) потока непосредственно перед входом в каналы рабочего колеса, V_O – скорость потока в предлопастном пространстве, на входе в рабочее колесо;

1 — место непосредствен­но после входа в канал, на входной кромке лопастей ра­бочего колеса;

2 – место непосредственно перед выходом из канала на выходной кромке лопастей колеса;

Скорость переносного движения U. Скорость точек рабочего колеса при переносном движении (2 – 2')равнаокружной скорости, пропорциональной радиусам точек и угловой скорости:

v_U = ωr = 2πnr_i /60

Окружная скорость направ­лена по касательной к окружности данного радиуса r (нормальна к радиусам, лежащим в плоскостях нормальных к оси).

Скорость относительного движения W. Направление относительной скорости потока воды (1 – 2) определяется формой лопастей ра­бочего колеса и меняется по мере прохождения воды через рабочее колесо. Величина относительной скорости зависит от расхода воды проходящей через турбину.

v_W = Q/s =Q/πDb

Физический смысл V_W. Возьмем около лопастей в сечениях входа и выхода колеса точки 1 и 2. Отложим векторы относительных скоростей W₁ и W₂. Вода здесь течет вдоль стенок, почему и векторы должны быть здесь направлены вдоль элементов осей каналов, (т.е. по касательным к входной кромке лопасти W₁ и выходной кромки лопасти W₂).

Следовательно, если размер b каналов вдоль оси колеса (высота колеса) постоянен, то отно­сительные скорости и их векторы обратно про­порциональны ширине каналов (шагу решетки t = 2πr / z_лоп).

При этом, скорости угловая ω а следовательно, и окружные u предполагаются заданными.

Абсолютная скорость V. Складывая геомет­рически по правилу параллелограмма векторы скоростей относительных W и окружных U, получаем векторы абсолютных скоростей V.

V = W + U

Следовательно, векторы скоростей V, U и Wобразуют треугольник скоростей в соответствующей точке потока.

На рисунке 4.5 построены треугольники скоростей для точки входа 1 и точки выхода 2.

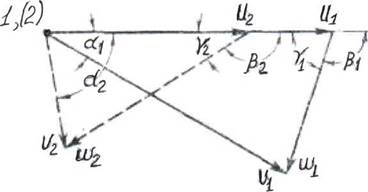Рисунок 4.5 Треугольник скоростей для входа и выхода.

Определяя значения и направления скоростей, эти векторы определяют и углы между ними.

Углы между векторами абсолютных скоростей V и окружных U обычно обозначаются через ά (ά₁ — на входе и ά₂ — на выходе). Углы ά можно было бы называть углами абсолютной скорости или струйными, они зависят от работы турбины, в первую очередь от открытия направляющего аппарата.

Углы между векторами относительных скоростей W и окружных U через β (β₁ — на входе и β₂ — на выходе), дополнительные к ним через γ. Тогда γ = 180 – β. Углы β — углы отно­сительной скорости или лопастные, они зависят от кон­струкции и формы лопастей. У радиально-осевых и пропеллерных турбин эти углы остаются неизменными при всех режимах работы турбины.

Таким образом, при анализе течения жидкости в рабочем колесе в первом прибли­жении предполагают:

1. Рабочее колесо имеет большое число бесконечно тонких лопа­стей, вследствие чего путь воды в относительном движении будет иметь форму лопасти АВ или средней струйки 1—2 (рис. 4.4);

2. Все скорости считаются средними в рассматриваемом сечении,
нормальном к общему направлению потока;

3. При расчетном режиме работы турбины имеет место безударный вход воды на лопасти рабочего колеса.

Следует отметить: на рисунке 4.4 показаны траектории абсолютного движения: А-В'—для частицы, вышедшей из точки А и пришедшей в точку В', и 1-2' —для частицы жидкости, вышедшей из точки 1 и пришедшей в точку 2'.

Векторы абсолютных скоростей V₁ и V₂ касательны к этим траекториям в начале (1) и в конце пути (2').

Векторы относительных скоростей W₁ и W₂ касательны в на­чальных и конечных точках траекторий относительного движения А-В или 1-2.

4.1.3.1 Кинематика потока в рабочем колесе осевых реактивных гидротурбин.

У осевых турбин поверхности тока в рабочем колесе близки к цилиндрическим (рисунок 4.6, а), т. е. расчетный диаметр D_Р можно вычислить как средний по площади:

Д_Р =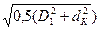

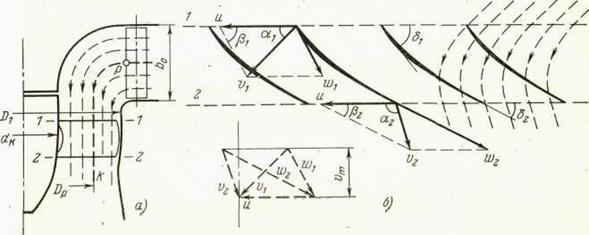
Рисунок 4.6. Поток в осевой турбине

Развертка цилиндрического сечения рабочего колеса показана на рисунке 4.6, б). Особенность состоит в том, что значение окружной скорости в точках 1 и 2 равны:

v_U = v _1U = v _2U = ωr = πD_Pn / 60

Меридианная составляющая абсолютной скорости v не изменяется от входа до выхода ( 1 – 2 ), тогда ее значение равно:

v_m = v_1m = v_2m =

Скорость на входных (1) и выходных (2) кромках опре­деляется как векторная сумма:

V₁ = V_1m + V_1u

Полученные в результате параллело­граммы скоростей показаны на рисунке 4.6, б). Треугольники скоростей на входной и выходной кромках совмещены (показаны пунктиром), поскольку они имеют одинаковые основание u и высоту v_m. Справа пунктирными линиями показаны траектории абсолютного движения жидкости в рабочем колесе.

ТЕКСТОВАЯ ИНФОРМАЦИЯ, ВЫЧИСЛЕНИЯ И ДЕЛОВАЯ ГРАФИКА