Движение потока в направляющем аппарате.
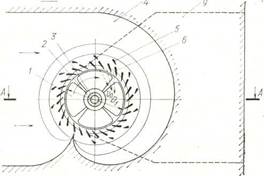
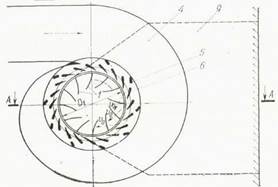
Во всех реактивных турбинах поток, поступающий на рабочее колесо, формируется направляющим аппаратом, представляющим собой круговую решетку профилей (лопаток), что хорошо видно на рисунке 4.2.
а) б)
Рисунок 4.2 Схемы турбин.
а– поворотно-лопастная; б – радиально-осевая.
Характерными показателями круговой решетки является форма профилей и густота решетки. Течение в пределах Н.А. является конфузорным* (конфузор (от лат. coniundo — вливаю, распределяю, смешиваю) — профилированный сужающийся канал, в котором дозвуковая скорость жидкости или газа возрастает в результате преобразования потенциальной энергии в кинетическую), а густая решетка лопаток обеспечивает практически полное совпадение направления потока на выходе, на диаметре D 02, с направлением профиля выходных участков лопаток. Положение лопатки характеризуется величиной открытия а0, которое определяет величину расхода и направление вектора V0. Скорость потока (рисунок 4.3) в радиальном направляющем аппарате, направленная по касательной к выходному участку лопатки, вектор V0 можно представить суммой двух слагаемых:
V0 = V0 R + V0 U
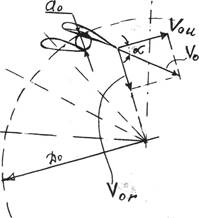 |  | ||
в которой V0 R— радиальная составляющая; V0 U — окружная составляющая.
Рисунок 4.3 Схема потока в направляющем аппарате.
Зная расход турбины Q=VS и размеры направляющего аппарата (D0, b0) радиальную компоненту определяем по формуле:
v0 R = Q/πD0b0
Угол между V0 и V0U обозначим ά0, тогда
vo = v0Rsinά0 ,
а окружную составляющую определяем из соотношения
vo u = v0cosά0.
Наличие окружной компоненты vou указывает на то, что поток за направляющим аппаратом «закручен» относительно оси в соответствии с профилем лопатки НА. Закрученность потока определяется величиной – циркуляция, обозначается Г, размерность м2/с.
Для осредненного потока за направляющим аппаратом, на его выходном диаметре D 02 циркуляция равна:
Г0 = π D02vo u = π D02v0cosά0
Отсюда следует, что направляющий аппарат создает циркуляцию потока.
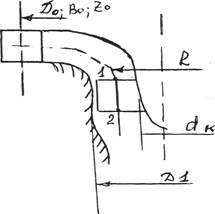
В пространстве (D 02 – 1) на рисунке 4.3, между концами направляющих лопаток и входными кромками лопастей рабочего колеса («предколесное или предлопастное» пространство) жидкость движется свободно, а траектория струек потока задается геометрией проточной части.
Важно понять как при этом изменяется скорость потока. Выделим в потоке элементарную массу m на радиусе R. Используя закон механики о моменте количества движения: «Для выделенной массы, производная по времени от момента количества движения относительно некоторой оси равна сумме моментов всех внешних сил, действующих на эту массу относительно той же оси». Этот закон представляется формулой:
d(mvouR)o /dt = ∑Mo ,
где: m – масса жидкости выделенного объема; vou окружная составляющая скорости; R – радиус; Мо – сумма моментов внешних сил, действующих на выделенную массу, относительно оси турбины О.
В итоге получим, что при свободном движении жидкости можно принять ∑МО = 0, а это значит, что mvouR = const. Отсюда вытекает важная зависимость:
vuR = const
Данное выражение определяет условия свободного движения жидкости в предлопастном пространстве и называется законом постоянства момента скорости.
С учетом того, что Г = 2π Rvu, получим условие постоянства циркуляции при свободном движении жидкости:
Г = ГО = const
Следовательно, в пространстве между направляющим аппаратом и рабочим колесом турбины циркуляция, созданная направляющим аппаратом сохраняется.
Дата добавления: 2015-02-16; просмотров: 1128;
