Тема 2. ПОТЕНЦИАЛ. РАБОТА. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ
Основные понятия и соотношения
Потенциалом электрического поля в данной точке называется скалярная величина 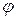 , равная отношению потенциальной энергии пробного заряда
, равная отношению потенциальной энергии пробного заряда 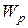 , помещенного в эту точку поля к величине пробного заряда
, помещенного в эту точку поля к величине пробного заряда 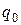 :
:
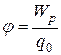 (35)
(35)
Связь между потенциалом электрического поля 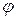 и напряженностью
и напряженностью 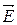 определяется соотношениями:
определяется соотношениями:
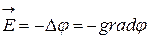 ; (36)
; (36)
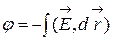 , (37)
, (37)
где 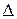 - дифференциальный оператор вида
- дифференциальный оператор вида
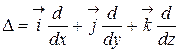 .
.
Эти соотношения позволяют найти напряженность поля 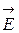 посредством дифференцирования потенциала
посредством дифференцирования потенциала 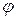 по координатам
по координатам 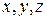 радиуса-вектора
радиуса-вектора 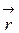 точки наблюдения, а также найти потенциал
точки наблюдения, а также найти потенциал 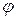 посредством интегрирования
посредством интегрирования 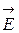 по
по 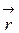 . Постоянная интегрирования при этом для конечной системы зарядов чаще всего определяется из условия равенства потенциала поля нулю на бесконечности. С учетом этого условия, потенциал поля точечного заряда
. Постоянная интегрирования при этом для конечной системы зарядов чаще всего определяется из условия равенства потенциала поля нулю на бесконечности. С учетом этого условия, потенциал поля точечного заряда 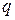
 в однородной и изотропной среде с диэлектрической проницаемостью
в однородной и изотропной среде с диэлектрической проницаемостью 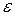 можно определить по формуле
можно определить по формуле
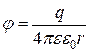 , (38)
, (38)
где 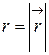 .
.
Следствием соотношений (36),(37) является условие ортогональности силовых линий поля эквипотенциальным поверхностям, уравнение которых определяется выражением
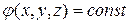 . (39)
. (39)
Другим следствием этих выражений является принцип суперпозиции, согласно которому потенциал электрического поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности. Следовательно, потенциал поля системы из 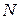 точечных зарядов
точечных зарядов 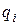 можно определить выражением
можно определить выражением
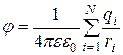 , (40)
, (40)
где 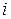 - номер заряда и
- номер заряда и 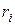 - расстояние от
- расстояние от 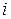 - го заряда до точки наблюдения.
- го заряда до точки наблюдения.
Из определения потенциала следует, что заряд 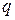 , находящийся в точке поля с потенциалом
, находящийся в точке поля с потенциалом 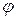 , обладает потенциальной энергией
, обладает потенциальной энергией
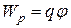 . (41)
. (41)
Следовательно, потенциальная энергия взаимодействия двух точечных зарядов равна
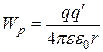 . (42)
. (42)
Нетрудно доказать, что потенциальная энергия взаимодействия системы точечных зарядов определяется выражением
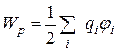 , (43)
, (43)
где 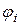 потенциал поля всех зарядов, кроме заряда
потенциал поля всех зарядов, кроме заряда 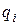 , в точке расположения заряда
, в точке расположения заряда 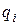 .Из последнего выражения следует, что проводник с зарядом
.Из последнего выражения следует, что проводник с зарядом 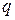 и потенциалом
и потенциалом 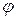 обладает потенциальной энергией
обладает потенциальной энергией
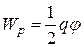 . (44)
. (44)
Уединенный проводник можно охарактеризовать понятием электрической емкости:
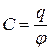 . (45)
. (45)
Это делает возможным выразить энергию заряженного проводника через величины 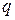 и
и 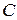 либо через величины
либо через величины 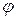 и
и 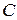 :
:
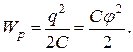 (46)
(46)
Система двух проводников с зарядами 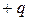 и
и 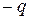 называется конденсатором. Эту систему можно охарактеризовать понятием взаимной емкости:
называется конденсатором. Эту систему можно охарактеризовать понятием взаимной емкости:
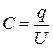 , (47)
, (47)
где 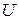 - разность потенциалов между проводниками.
- разность потенциалов между проводниками.
Потенциальная энергия заряженного конденсатора может быть найдена с помощью выражений
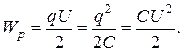 (48)
(48)
Энергия заряженных тел - это энергия их электрического поля. Выражая ее через характеристики поля, можно получить
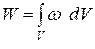 , (49)
, (49)
где 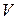 объем поля, а
объем поля, а 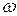 - плотность энергии поля, которая выражается через векторы напряженности
- плотность энергии поля, которая выражается через векторы напряженности 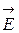 и электрического смещения
и электрического смещения 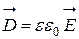 :
:
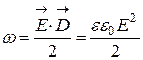 . (50)
. (50)
Работа электрических сил при перемещении заряда 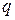 из точки поля с потенциалом
из точки поля с потенциалом 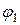 в точку с потенциалом
в точку с потенциалом 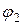 равна
равна
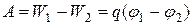 . (51)
. (51)
В заключение приведем таблицу, в которой собран ряд формул, связанных с вычислением потенциала и потенциальной энергии электрического поля.
Таблица 2
| Физическая величина | Формула | Обозначения |
Связь напряженности 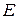 и потенциала и потенциала 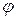 в одномерном случае в одномерном случае
| 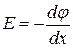
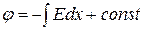
| 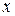 - координата оси; - координата оси;
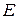 - проекция вектора напряженности электрического поля на ось - проекция вектора напряженности электрического поля на ось 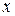
|
Связь 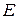 и и 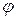 в трёхмерном сферически-симметричном случае. в трёхмерном сферически-симметричном случае.
| 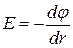
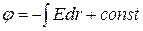
| 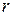 - расстояние от начала координат; - расстояние от начала координат;
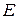 - проекция вектора напряженности электрического поля на направление вектора - проекция вектора напряженности электрического поля на направление вектора 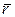
|
| Потенциал заряженной плоскости | 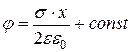
| 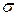 - поверхностная плотность заряда плоскости; - поверхностная плотность заряда плоскости;
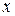 - расстояние от плоскости до точки, в которой определяется потенциал - расстояние от плоскости до точки, в которой определяется потенциал
|
| Потенциал заряженной нити | 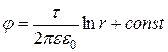
| 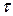 - линейная плотность заряда нити; - линейная плотность заряда нити;
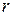 - расстояние от нити до точки, в которой определяется потенциал - расстояние от нити до точки, в которой определяется потенциал
|
| Потенциал заряженной проводящей сферы | 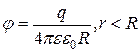
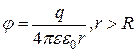
| 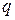 - заряд сферы; - заряд сферы;
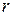 - расстояние от центра сферы; - расстояние от центра сферы;
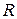 - радиус сферы - радиус сферы
|
| Энергия заряженной проводящей сферы | 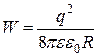
| 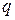 - заряд сферы; - заряд сферы;
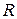 - радиус сферы - радиус сферы
|
| Энергия плоского конденсатора | 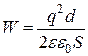
| 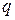 - заряд конденсатора; - заряд конденсатора;
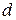 - расстояние между обкладками; - расстояние между обкладками;
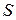 - площадь обкладок - площадь обкладок
|
| Емкость сферического проводника | 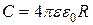
| 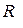 - радиус сферического проводника - радиус сферического проводника
|
| Емкость плоского конденсатора | 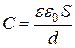
| 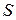 - площадь обкладок; - площадь обкладок;
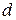 - расстояние между обкладками - расстояние между обкладками
|
Дата добавления: 2015-02-16; просмотров: 1394;
