Определение оптимального уровня денежных средств

Определение оптимального остатка денежных средств (совокупного остатка на счетах и в кассе) также представляет собой одну из основных задач финансового менеджера. Сточки зрения теории инвестирования денежные средства представляют собой один из частных случаев инвестирования в товарно-материальные ценности. Поэтому к ним применимы общие требования. Во-первых, необходим базовый запас денежных средств для выполнения текущих расчетов. Во-вторых, необходимы определенные денежные средства для покрытия непредвиденных расходов. В-третьих, целесообразно иметь определенную сумму свободных денежных средств, чтобы обеспечить возможное или прогнозируемое расширение деятельности.

Таким образом, к денежным средствам можно применить модели, разработанные в теории управления запасами и позволяющие оптимизировать величину денежных средств. Речь идет о том, чтобы оценить: а) общий объем денежных средств и их эквивалентов; б) какую их долю следует держать на расчетном счете, а какую в виде быстро реализуемых ценных бумаг; в) когда и в каком объеме осуществлять взаимную трансформацию денежных средств и быстро реализуемых активов.

В западной практике наибольшее распространение получили модель Баумоля и модель Миллера-Орра.

Суть модели Баумоля заключается в следующем. Предполагается, что предприятие начинает работать, имея максимальный и целесообразный для него уровень денежных средств, и затем постоянно расходует их в течение некоторого периода времени. Все поступающие средства от реализации товаров и услуг предприятие вкладывает в краткосрочные ценные бумаги. Как только запас денежных средств истощается, т.е. становится равным нулю или достигает некоторого заданного уровня безопасности, предприятие продает часть ценных бумаг и тем самым пополняет запас денежных средств до первоначальной величины. Таким образом, динамика остатка средств на расчетном счете представляет собой «пилообразный» график (рис.9.2.)

Остаток средств

на расчетном счете

Q

Q/2

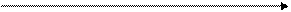
Время

Рис. 9.2. График изменения остатка средств на расчетном счете (модель Баумоля)

Сумма пополнения (Q) вычисляется по формуле:

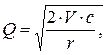(9.7.)

где V – прогнозируемая потребность в денежных средствах в периоде (год, квартал, месяц);

c – расходы по конвертации денежных средств в ценные бумаги;

r – приемлемый и возможный для предприятия процентный доход по краткосрочным финансовым вложениям.

Таким образом, средний запас денежных средств составляет Q/2, а общее количество сделок по конвертации ценных бумаг в денежные средства (k) равно:

k = V : Q. (9.8.)

Общие расходы (ОР) по реализации такой политики управления денежными средствами составляет:

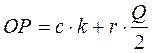. (9.9.)

Первое слагаемое в этой формуле представляет собой прямые расходы, второе – упущенная выгода от хранения средств на расчетном счете вместо того, чтобы инвестировать их в ценные бумаги.

Модель Баумоля проста и в достаточной степени приемлема для предприятий, денежные расходы которых стабильны и прогнозируемы. В действительности такое случается редко; остаток средств на расчетном счете изменяется случайным образом, причем возможны значительные колебания.

Модель, разработанная Миллером и Орром, представляет собой компромисс между простотой и реальностью. Она помогает ответить на вопрос: как предприятию следует управлять своим денежным запасом, если невозможно предсказать каждодневный отток или приток денежных средств? Миллер и Орр используют при построении модели процесс Бернулли – стохастический процесс, в котором поступление и расходование денег от периода к периоду являются независимыми случайными событиями.

Логика действий финансового менеджера по управлению остатком средств на расчетном счете заключается в следующем. Остаток средств на счете хаотически меняется до тех пор, пока не достигает верхнего предела. Как только это происходит, предприятие начинает покупать достаточное количество ценных бумаг с целью вернуть запас денежных средств к некоторому нормальному уровню (точке возврата). Если запас денежных средств достигает нижнего предела, то в этом случае предприятие продает свои ценные бумаги и таким образом пополняет запас денежных средств до нормального предела.

При решении вопроса о размахе вариации (разность между верхним и нижним пределами) рекомендуется придерживаться следующей политики: если ежедневная изменчивость денежных потоков велика или постоянные затраты, связанные с покупкой и продажей ценных бумаг, высоки, то предприятию следует увеличить размах вариации и наоборот. Также рекомендуется уменьшить размах вариации, если есть возможность получения дохода благодаря высокой процентной ставке по ценным бумагам.

Реализация модели осуществляется в несколько этапов.

1. Устанавливается минимальная величина денежных средств (О_Н), которую целесообразно постоянно иметь на расчетном счете (она определяется экспертным путем исходя из средней потребности предприятия в оплате счетов, возможных требований банка и др.).

2. По статистическим данным определяется вариация ежедневного поступления средств на расчетный счет (v).

3. Определяются расходы (Р_Х) по хранению средств на расчетном счете (обычно их принимают в сумме ставки ежедневного дохода по краткосрочным ценным бумагам, циркулирующим на рынке) и расходы (Р_Т) по взаимной трансформации денежных средств и ценных бумаг (эта величина предполагается постоянной).

4. Рассчитывают размах вариации остатка денежных средств на расчетном счете (S) по формуле:

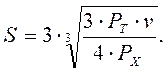(9.10.)

5. Рассчитывают верхнюю границу денежных средств на расчетном счете (О_В), при превышении которой необходимо часть денежных средств конвертировать в краткосрочные ценные бумаги:

О_В = О_Н + S. (9.11.)

6. Определяют точку возврата (Т_В) – величину остатка денежных средств на расчетном счете, к которой необходимо вернуться в случае, если фактический остаток средств на расчетном счете выходит за границы интервала (О_Н, О_В):

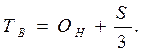(9.12.)