Уравнение параболической регрессии

В некоторых случаях эмпирические данные статистической совокупности, изображенные наглядно с помощью координатной диаграммы, показывают, что увеличение фактора сопровождаются опережающим ростом результата. Для теоретического описания такого рода корреляционной взаимосвязи признаков можно взять уравнение параболической регрессии второго порядка:

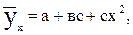(11.16)

где 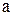, – параметр, показывающий среднее значение результативного признака при условии полной изоляции влияния фактора (х=0); 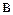– коэффициент пропорциональности изменения результата при условии абсолютного прироста признака-фактора на каждую его единицу; с – коэффициент ускорения (замедления) прироста результативного признака на каждую единицу фактора.

Положив в основу вычисления параметров 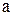, , 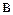с способ наименьших квадратов и приняв условно срединное значение ранжированного ряда за начальное, будем иметь Σх=0, Σх³=0. При этом система уравнений в упрощенном виде будет:

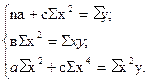
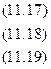
Из этих уравнений можно найти параметры 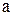, , 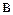с, которые в общем виде можно записать так:

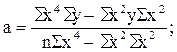(11.20)

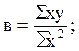(11.21)

(11.22)

Отсюда видно, что для определения параметров 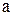, , 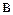с необходимо рассчитать следующие значения: Σ у, Σ ху, Σ х² , Σ х² у, Σ х⁴. С этой целью можно воспользоваться макетом табл. 11.9.

Допустим, имеются данные об удельном весе посевов картофеля в структуре всех посевных площадей и урожае (валовом сборе) культуры в 30 сельскохозяйственных организациях. Необходимо составить и решить уравнение корреляционной взаимосвязи между этими показателями.

Т а б л и ц а 11.9. Расчет вспомогательных показателей для уравнения