Общие понятия о земной поверхности, формах и размерах Земли.
1. Физическая поверхность Земли.
2. Координаты местности.
3. Абсолютные и относительные высоты местности.
1.При решении геодезических задач требуется знать форму и размеры Земли. Земля не является правильным геометрическим телом. Ее физическая поверхность и в особенности поверхность суши очень сложная (рис. 1), и ее невозможно выразить какой-либо математической формулой.
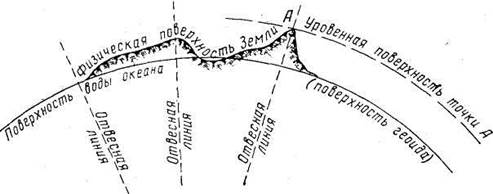
Поэтому в геодезии введено понятие уровенной поверхности. Уровенной поверхностью называют выпуклую поверхность, перпендикулярную к направлению силы тяжести (отвесной линии) в каждой точке. Поверхность Мирового океана, мысленно продолженная под сушей, названа поверхностью геоида. Но и поверхность геоида из-за неравномерного размещения масс в теле Земли также очень сложная и не выражается какой-либо математической поверхностью, например поверхностью шара. Под формой Земли в геодезии принято понимать поверхность воды в морях и океанах, находящейся в спокойном состоянии, продолженную под материки. Во всех точках эту поверхность пересекают отвесные линии под углом 900.
Исследования показали, что Земля сплюснута у полюсов, поэтому в качестве математической поверхности, характеризующей форму Земли, принимают поверхность такого эллипсоида вращения (сфероида), т.е. тела, получающегося от вращения эллипса вокруг его малой оси, которая по форме близко подходит к поверхности геоида.
Определением размеров земного эллипсоида занимались многие ученые разных стран. Советские геодезисты в 1942 г. под руководством проф. Ф.Н. Красовского закончили вычисления и получили новые размеры эллипсоида Земли: большая полуось а = 6 378 245 м,
малая полуось b = 6 356 863 м,
полярное сжатие α = (a-b)/а = 1/298,3
2. Положение точек земной поверхности на карте и плане определяется координатами. Наиболее употребительны географические и прямоугольные координаты.
Географическими координатами являются широта и долгота точки. Гео- графической широтой φ точки М называют угол, составленный отвесной линией, проходящей через эту точку, и плоскостью экватора (рис. 2), а географической долготой — двугранный угол, заключенный между плоскостью меридиана, проходящего через эту точку, и плоскостью начального меридиана. Широты бывают северная и южная, изменяются от 0° (на экваторе) до 90° (на земных полюсах). Долготы бывают восточная и западная, изменяются от 0° (на начальном — гринвичском меридиане) на восток и на запад до 180° (на тихоокеанской ветви гринвичского меридиана. Линия, проходящая через точки с одинаковыми широтами, называется naраллелъю, а с одинаковыми долготами — меридианом.
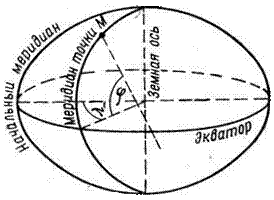
Угол, составленный нормалью к поверхности эллипсоида и плоскостью экватора называется геодезической широтой, а двугранный угол, заключенный между плоскостями геодезического и начального меридианов, — геодезической долготой.
Если для составления карты на большую территорию строят географическую сетку меридианов и параллелей, то для составления планов и карт в инженерной геодезии чаще всего пользуются системой прямоугольных координат. Положение точки определяется относительно оcей прямоугольных координат: оси абсцисс хх и оси ординат уу. Система прямоугольных координат в геодезии повернута относительно системы прямоугольных координат, принятых в математике, на 90°, после чего еще повернута около оси абсцисс на 180° (зеркальное изображение). При таком расположении осей углы в геодезии для ориентирования линий, как увидим ниже, отсчитывают от вертикальной оси по ходу часовой стрелки, тогда как углы в тригонометрии отсчитывают от горизонтальной оси против хода часовой стрелки. Благодаря этому формулы тригонометрии и аналитической геометрии полностью применимы в геодезии. В связи с этим четверти системы координат в геодезии пронумерованы по ходу часовой стрелки. Положение каждой точки определяется абсциссой х и ординатой у. Знаки координат зависят от четверти, в которой находится точка (табл. 1).
| Четверти | X | Y |
| рроо | + | + |
| II | + | |
| III | ||
| IV | + | ■— |
Для небольших участков система прямоугольных координат может иметь частное начало в любом месте участка. В государственной системе за ось ординат принимают линию экватора, аза ось абсцисс — меридиан, принимаемый за осевой.
Помимо осей координат, на бумаге через определенные расстояния проводят линии, параллельные осям координат (через километр, полкилометра и др.), составляющие координатную сетку. Эта сетка нужна как для составления плана, так и для пользования им.
Многие карты, используемые в инженерных целях, кроме географической сетки, имеют и прямоугольную координатную сетку. Существуют и формулы для перечисления географических координат в прямоугольные и обратно.
Положение точки по высоте (в третьем измерении) характеризуется координатой — отметкой. Отметки надписывают на планах и картах или выражают условными обозначениями.
3.При использовании изображения земной поверхности на бумаге (плане или карте) для составления проекта оросительных или осушительных систем, размещения земельных участков для механизированной обработки и др. требуется иметь не только очертания объектов в горизонтальной проекции, но и получать по плану (карте) представление о неровностях земной поверхности, о крутых и пологих местах, о том, на сколько одна точка расположена выше или ниже другой.
Неровности земной поверхности характеризуются высотами точек. Высотой точки называют отрезок отвесной линии (расстояние) от этой точки до уровенной поверхности, принятой за начало счета высот (рис. 2). Числовое значение высоты называют отметкой точки.
Если отметку точки определяют относительно уровенной поверхности океана или моря, то отметка называется абсолютной, если же относительно какой-либо уровенной поверхности, проходящей через произвольную точку, то отметка называется относительной, или условной.
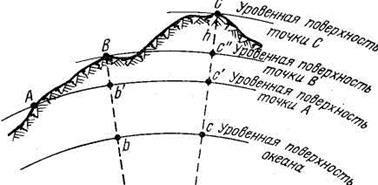
Рис. 2
На рис. 2 отрезки Вb/ и Сс/ представляют абсолютные отметки соответственно точек В и С земной поверхности, а отрезки Вb/ и Сс' — условные отметки этих точек. Отметки точек нередко называют высотами, или альтитудами. Обычно отметки точек обозначают буквой Н. Например, Нв означает отметку точки В. Разность между отметками точек называется превышением, которое обычно обозначается буквой h. Например, отрезок Сс" есть превышение точки С над точкой В. Превышение в направлении от точки В к точке С положительно, а поэтому число, выражающее превышение, сопровождают знаком плюс; превышение в направлении от точки С к точке В — отрицательно и сопровождается знаком минус.
Абсолютные отметки точек земной поверхности преимущественно положительные и лишь для точек, располагающихся ниже уровенной поверхности океана, например на Каспийской низменности, отрицательные, где они доходят до —28 м. В СССР началом счета абсолютных отметок служит нуль Кронштадтского футштока, на котором чертой отмечен средний уровень воды в Финском заливе.
Отметка точки последующей равна отметке данной точки плюс соответствующее превышение: НВ = НА + h.
Дата добавления: 2015-02-13; просмотров: 1860;
