Лекция № 5

ТОЧНОСТЬ КАРТ И ПЛАНОВ. МАСШТАБЫ

1. Понятие точности измерения и его отображения на карте и плане.

2. Понятие масштаба, виды масштабов.

3. Численный масштаб.

4. Линейный масштаб.

5. Поперечный масштаб

1. Предельная и графическая точности масштабов.При оценке точ­ности нанесения точек на план следует исходить из физиологических возможностей человеческого глаза. Как известно, глаз человека спосо­бен отчетливо различать две точки, если они располагаются под утлом не менее 60" к наблюдателю. При меньшем угле зрения глаз восприни­мает две точки слившимися в одну. Расстоянию наилучшего зрения, равному 25 см, углу в 60 " соответствует отрезок, равный 0,1 мм. Таков, например, диаметр кружка от укола остро отточенной иглы. Отсюда следует, что на плане (карте) в самом благоприятном случае можно изобразить лишь такие горизонтальные проекции линий местности, которым в данном масштабе соответствует отрезок 0,1 мм и более.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм (0,01см) на плане, называется предельной точностью масштаба.

Практически принимается, что длина отрезка на плане или карте может быть оценена с точностью 0,2 мм.

Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм (0,02 см) на плане, называется графической точностью масштаба.

Значения предельной и графической точностей различных числен­ных масштабов, найденные по формулам (17) и (18), приведены ниже.

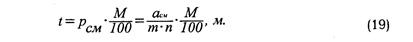
Такая точность определения расстояний на плане или карте не мо­жет быть достигнута при использовании линейного масштаба. Поэто­му для повышения точности измерений расстояний на плане или карте применяют поперечный (трансверсальный)масштаб.

2. Масштаб- это отношение длины линии на чертеже, плане, карте l к длине горизонтального проложения, соответствующей линии местности S:

М = l/ S.

При выполнении съемок, составлении геодезических чертежей и при работе с ними приходится пользоваться следующими видами масштабов: численным, пояснительным, линейным, поперечным, переводным.

Иначе говоря, масштаб - это коэффициент подобия, поскольку составление чертежа представляет собой подобное преобразование ортогональной проекции местности, полученной на горизонтальной плоскости.

На профилях различают еще вертикальный численный масштаб, относящийся к высотным элементам проекции.

3. Численный масштаб записывают в виде правильной дроби, у которой числитель единица, а знаменатель показывает степень уменьшения линейных размеров на плане. В метрической системе мер пользуются такими масштабами: 1:500, 1:1000, 1:2000, 1:5000, 1:10 000 и т.д. При сравнении двух или нескольких масштабов между собой надо иметь в виду, что чем больше знаменатель, тем, крупнее масштаб плана, и на таком плане изобразится больше мелких деталей, а измерение линий по нему можно сделать с большей точностью. Следовательно, масштаб 1:5000 крупнее 1:10 000, но мельче 1:2000. Например, численный масштаб 1:1000 показывает, что все горизонтальные проложения линий местности при перенесении их на план уменьшены в 1000 раз, то есть отрезок в 1 см на плане соответствует линии в 1000 см (10 м) на местности

Пример 1: Длина линии на плане масштаба 1:5000 равна 4 см. Определить ее длину на местности. Решение: 4х5000=20000 см = 200 м.

Пример 2: Если горизонтальное проложение линии местности равно 283,7 м, масштаб 1:5000, т.е. в сантиметре 50 м, то длина линии на плане будет 283,7:50 = 5,67 см.

4. Линейный масштаб представляет собой шкалу, деления которой подписаны применительно к заданному численному масштабу. Им пользуются при нанесении проекции линий на чертеж, а также при измерении линий на чертеже с целью определения соответствующей им длины на проекции. Применение линейного масштаба избавляет от вычислений, выполняемых при пользовании численным масштабом. Хотя эти вычисления просты, но при большом их количестве становятся утомительными и отнимают много времени.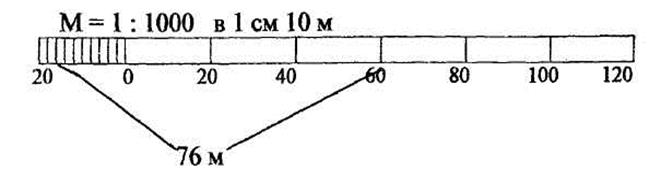

Рисунок 1 – Линейный масштаб

Для построения метрического линейного масштаба берут прямую линию и откладывают на ней несколько раз (четыре-пять) один и тот же отрезок (1-2 см), называемый основанием масштаба (рис.1). Первое основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которое на проекции соответствует в заданном масштабе основанию. Вправо от нуля деления масштаба подписывают соответственно расстояниям на местности, выраженным отрезками от нуля до штриха с подписью. В качестве основания для метрических масштабов чаще всего берут отрезок в 2 см. При работе в масштабе 1:1000 и основании, равном 2 см, линейный масштаб подписывают так, как это указано на рис. 1.

При этом масштабе 2 см на бумаге соответствует 2000 см или 20 м на местности, а 1 см — соответственно 1000 см или 10 м.

При пользовании линейным масштабом правую ножку циркуля ставят на нулевое деление или на одно из делений справа от нуля в зависимости от того, меньше или больше одного основания нужно измерить или отложить линию. Левая ножка циркуля располагается либо на делении с нулевой подписью, если длина линии содержит целое число оснований, либо в пределах первого основания, имеющего мелкие деления, с оценкой на глаз десятых долей этих делений. По горизонтальным размерным линиям легко сообразить, где находились ножки циркуля, когда брали тот или иной отрезок. Видно также, что каждый отрезок составляется из двух частей: от нуля до правой ножки циркуля и от нуля до левой ножки его.

При откладывании с помощью измерителя круглых чисел 20, 40 м и т. д. одна ножка измерителя устанавливается на нулевое деление, а вторая — на деление с соответствующей надписью. Каждое деление первого основания слева равно: 20 м : 10 = 2 м. Чтобы отложить, например, 76 м, надо одну ножку измерителя поставить на деление 60, а вторую на восьмое деление от нуля слева (8 х 2 м = 16 м). В итоге получается: 60 м + 16 м = 76 м. Десятые доли метра определяются на глаз (рис. 1).

Применение простого линейного масштаба ограничено вследствие сравнительно небольшой его точности, поэтому для составления точных планов и карт пользуются преимущественно поперечным масштабом.

5. Поперечный масштаб применяют для того, чтобы избежать оценки на глаз долей делений первого основания и в результате повысить точность измерений и построений на чертежах. Обычно пользуются поперечными

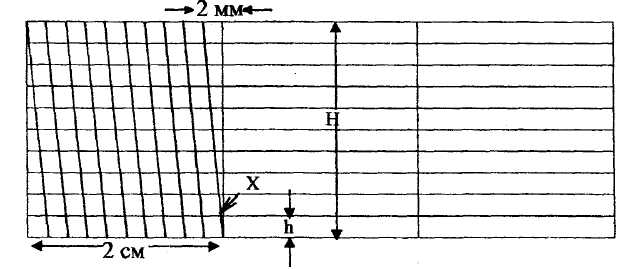
Рисунок 2 – Поперечные масштаб

масштабами, награвированными на тонких металлических пластинках или на транспортирах. Поперечный масштаб строится в виде прямоугольника длиной 8-10 см и высотой 2-3 см. В случае надобности поперечный масштаб для заданного численного можно построить (рис.2) следующим образом.

На горизонтальной прямой, как и при построении линейного масштаба, откладывают несколько раз основание (6-10 отрезков, обычно 2 см) и первый отрезок делят на 10 равных частей (обычно в 2 мм). Полученные деления подписывают подобно тому, как это делалось при построении линейного масштаба. Из концов всех оснований проводят вверх вертикальные линии; на крайних линиях откладывают по 10 одинаковых отрезков, например, по 2 мм каждый; полученные в результате этого точки соединяют горизонтальными прямыми. Верхнюю линию первого основания делят на десять равных частей и к ранее нанесенным делениям внизу, на первом основании, проводят косые линии, называемые трансверсалями, как показано на рис.2. Между косыми параллельными линиями заключены горизонтальные отрезки, равные десятой доле основания каждой в отдельности. Между нулевой вертикальной линией и смежной с ней косой линией заключаются отрезки от одной до десяти десятых наименьшего деления основания или от одной до десяти сотых самого основания, т.е. как раз то, что приходится отсчитывать на глаз по линейному масштабу. Значение мелких делений подписано у крайней левой вертикальной линии масштаба, что облегчает пользование им.

Основание самого большого треугольника равно 2 мм. Основание (Х) самого маленького треугольника называется наименьшим делением поперечного масштаба.

Если высоту большого треугольника обозначить буквой Н, а маленького треугольника h, то из соотношения 2/Н=Х/h, получается, что

Х=(2· h)/Н; но h=Н/10,

тогда Х=(2·Н)/(Н·10)=0,2 мм

Каждая от откладываемых по масштабу линий слагается из трех частей:

1) количества целых основания, взятых от нулевой вертикальной линии до правой ножки циркуля;

2) десятых долей основания, взятых между косыми линиями от проходящей через нуль до левой ножки циркуля;

3) сотых долей основания, расположенных между вертикальной и косой линиями, выходящими из нулевой точки масштаба.

Пользуясь поперечным масштабом, нужно следить за тем, чтобы при отложении или измерении отрезка концы обеих ножек циркуля всегда находились на одной и той же горизонтальной линии масштаба.

Масштабы, награвированные на пластинках или на транспортирах, следует разметить соответственно тому численному масштабу, в котором составлен или будет составляться чертеж.

Предельной точностью масштаба называется отрезок на проекции местности, который соответствует наименьшему делению поперечного масштаба, т.е. одной сотой основания его. Наименьшее деление поперечного масштаба равно 0,2 мм или 1/100 основания масштаба.