Сложение двух одинаково направленных гармонических колебаний.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты w. Смещение Х (результирующее колебание) будет суммой смещений Х₁ и Х₂, которые запишутся следующим образом

Х₁ = А₁Cos(w t + a₁) Х₂ = А₂Cos(w t + a₂) ,

где А₁ и А₂ - амплитуды колебаний, w - циклическая частота,

a₁ и a₂ - начальные фазы.

Результирующее колебание равно: Х = Х₁ + Х₂.

Представим оба колебания с помощью векторов 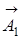и

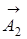
Y

А₁

А₂

y₂ y

A₁

a₂ a

a₁ y₁

Х₁ Х₂

Х

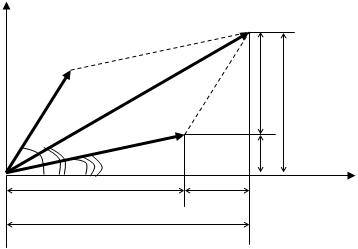
Рис.1.

Построим по правилам сложения векторов результирующий вектор 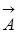. Видно, что проекция этого вектора на ось Х равна сумме проекций слагаемых векторов

Х = Х₁ + Х₂

Следовательно, вектор 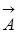представляет собой амплитуду результирующего колебания. Этот вектор вращается с той же угловой скоростью w, как и вектора 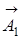и 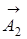, так что результирующее движение будет гармоническим колебанием с частотой w, амплитудой А и начальной фазой a. Из построения (рис.1) видно, что

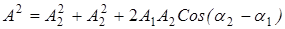
(1)

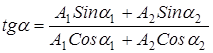
Итак, представление гармонических колебаний посредством векторов дает возможность свести сложение нескольких колебаний к операции сложения векторов. Этот прием бывает особенно полезен, например, в оптике, где световые колебания в некоторой точке определяются как результат наложения многих колебаний, приходящих в данную точку от различных участков волнового фронта.

Биения.

Особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличают по частоте. Результирующее движение при этих условиях можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такое колебание называется биением.

Обозначим частоту одного из колебаний w , частоту второго колебания w + Dw. По условию Dw<<w. Амплитуды обоих колебаний будем полагать одинаковыми и равными А. Начальные фазы колебаний пусть будут равны нулю. Тогда уравнения колебаний имеют вид

Х₁ = АCos wt Х₂ = АCos (w + Dw) t,

складывая эти выражения, и проведя преобразования, получим

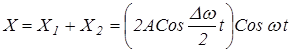
(во втором множителе пренебрегаем членом 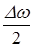по сравнению с w). График результирующего колебания x изображен на рис.2 для случая Dw /w = 10.

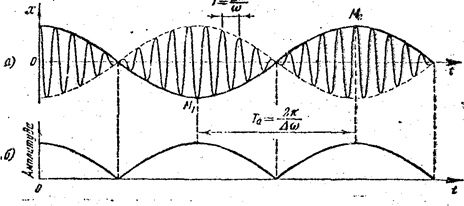
Рис.2.