Порядок выполнения работы. 1. Аналитический метод определения передаточного отношения сложного зубчатого механизма.
1. Аналитический метод определения передаточного отношения сложного зубчатого механизма.
Общее передаточное отношение 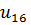 представляют как произведение передаточного отношения планетарного редуктора
представляют как произведение передаточного отношения планетарного редуктора 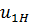 и передаточного числа зубчатого ряда
и передаточного числа зубчатого ряда 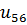 =
= 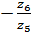 :
:
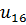 =
= 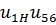
Для определения передаточного отношения планетарного механизма используют метод обращенного движения. Для этого мысленно сообщают дополнительное вращение механизму со скоростью, равной скорости водила, но в противоположном направлении. В результате водило Н окажется неподвижным, а передаточное отношение при неподвижном водиле от ведущего колеса с числом зубьев 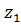 к ведомому колесу с числом зубьев
к ведомому колесу с числом зубьев 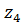 определют по формуле:
определют по формуле:
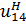 =
= 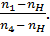
Имея в виду, что число оборотов неподвижного колеса 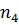 = 0, решают это уравнение относительно
= 0, решают это уравнение относительно 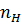 :
:
- 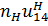 =
= 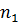 -
- 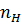 или
или 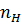 =
= 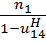
Передаточное отношение 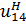 при неподвижном водиле определяют как для простой зубчатой передачи через числа зубьев колес:
при неподвижном водиле определяют как для простой зубчатой передачи через числа зубьев колес:
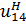 = (
= ( 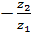 ) (
) ( 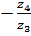 )
)
Передаточное отношение данного планетарного механизма будет равно:
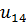 =
= 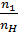 = 1
= 1 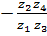
2. Графоаналитический метод определения передаточного отношения.
Размеры зубчатых колес зависят от модуля и числа зубьев. Для нулевых колес начальная окружность совпадает с делительной, радиус которой определятся по формуле
r = 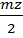 ,
,
где m – модуль зубчатых колес, мм;
z – число зубьев колеса.
Подставляя величину модуля и числа зубьев, вычисляют радиусы начальных окружностей всех колес и вычерчивают две проекции кинематической схемы механизма в масштабе 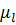 ,
, 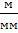 (рис. 8).
(рис. 8).
За линию отсчетов принимают вертикальную линию, на которую проецируют оси вращения всех колес и точки соприкосновения зубьев соседних колес.
Зная число оборотов первого колеса определяют скорость точки А:
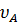 =
= 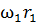 =
= 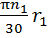 ,
, 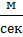 .
.
Выбирая отрезок, изображающий скорость в точке А, 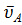 = (60-120) мм, вычисляют масштаб скорости
= (60-120) мм, вычисляют масштаб скорости 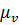 =
= 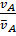 ,
, 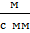 .
.
Откладывают от точки А перпендикулярно вертикальной прямой вектор скорости 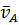 . Скорость точки О равна 0. Зная скорости двух точек колеса
. Скорость точки О равна 0. Зная скорости двух точек колеса 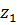 (точки О и А), проводят линию распределения линейных скоростей для этого колеса -
(точки О и А), проводят линию распределения линейных скоростей для этого колеса - 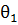 линию (рис. 8).
линию (рис. 8).
Рассматривая движение сателлита, состоящего из колес 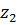 -
- 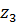 , видно, что точка А одновременно принадлежит колесу
, видно, что точка А одновременно принадлежит колесу 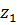 и колесу
и колесу 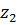 , а точка В одновременно принадлежит колесу
, а точка В одновременно принадлежит колесу 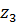 и колесу
и колесу 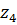 . Скорость точки В равна нулю, так как колесо
. Скорость точки В равна нулю, так как колесо 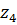 неподвижно. Следовательно, для сателлита
неподвижно. Следовательно, для сателлита 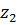 -
- 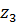 известны скорости двух (точек А и В); через конец вектора скорости точки А и точку В на вертикальной линии проводим линию распределения скоростей сателлита
известны скорости двух (точек А и В); через конец вектора скорости точки А и точку В на вертикальной линии проводим линию распределения скоростей сателлита 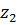 -
- 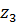 -
- 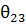 линию. Конец вектора скорости точки
линию. Конец вектора скорости точки 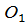 , принадлежащий сателлиту
, принадлежащий сателлиту 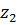 -
- 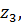 будет находиться также на линии
будет находиться также на линии 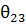 . Для этого из точки
. Для этого из точки 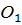 на вертикальной линии проводят перпендикулярно вектор скорости
на вертикальной линии проводят перпендикулярно вектор скорости 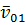 до пересечения с линией
до пересечения с линией 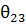 .
.
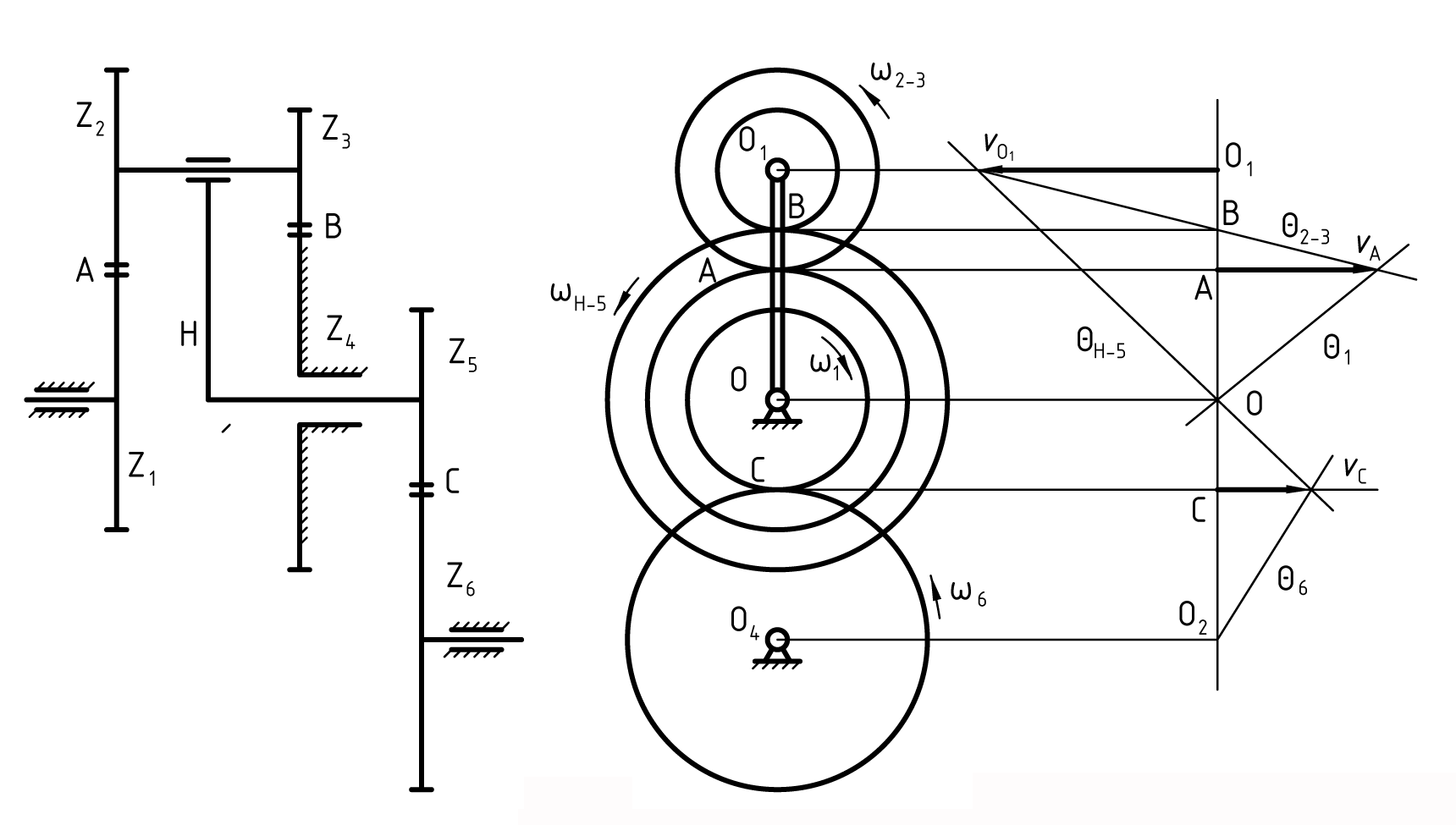
Рис. 8 Кинематическая схема сложного зубчатого механизма в двух проекциях с планом скоростей
Далее рассматривают движение водила Н и жестко связанного с ним колеса 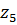 . Зная скорости двух точек: водила – точки
. Зная скорости двух точек: водила – точки 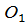 и точки О, скорость которой равна нулю, проводят линию
и точки О, скорость которой равна нулю, проводят линию 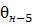 . Это будет линия распределения скоростей для водила Н и колеса
. Это будет линия распределения скоростей для водила Н и колеса 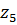 , на которой находится конец вектора
, на которой находится конец вектора 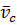 скорости точки С.
скорости точки С.
Рассматривая движение колеса 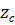 , проводят линию
, проводят линию 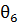 через конец вектора
через конец вектора 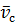 и ось вращения колеса
и ось вращения колеса 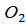 .
.
Переходят к построению плана угловых скоростей. Угловая скорость колеса 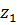 определяется по формуле:
определяется по формуле:
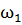 =
= 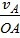 =
= 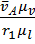 =
= 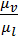 tg
tg 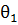
Из этой формулы видно, что угловая скорость звена пропорциональна тангенсу угла между вертикальной линией и линией 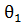 .
.
Для построения планов угловых скоростей проводят перпендикулярно линии отсчета линейных скоростей горизонтальную линию. На этой линии из произвольной точки Р опускают перпендикуляр и отмечают на нем расстояние РК = h. Через полученную точку К проводят лучи параллельные соответствующим θ -линиям из плана линейных скоростей до пересечения с линией в точках I, 2-3, Н-5,6 (рис 9).
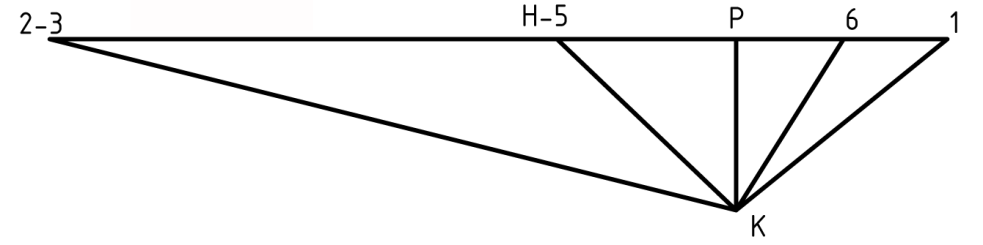
Рис. 9 План угловых скоростей сложного зубчатого механизма
Масштаб плана угловых скоростей определяют по формуле:
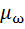 =
= 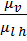 , I/ с мм.
, I/ с мм.
Отрезки на горизонтальной линии (рис.9) 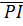 ,
, 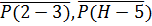 ,
, 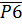 изображают в масштабе
изображают в масштабе 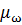 угловые скорости соответствующих звеньев. Так, например, угловая скорость
угловые скорости соответствующих звеньев. Так, например, угловая скорость 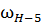 и число оборотов
и число оборотов 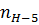 на выходе планетарного механизма будет:
на выходе планетарного механизма будет:
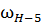 =
= 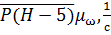 ,
,
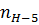 =
= 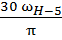 ,
, 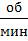 .
.
Для колеса 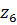 соответственно
соответственно
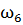 =
= 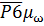 ,
,  ,
,
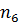 =
= 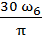 ,
, 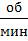 .
.
Направление вращения колес определяют следующим образом: звенья, для которых соответствующие точки на горизонтальной линии лежат вправо от точки Р (точки 1 и 6), вращаются по часовой стрелке, а звенья, для которых точки лежат влево от точки Р (точки 2-3, Н-5), вращаются против часовой стрелки (рис. 9).
3. Передаточное отношение сложного зубчатого механизма
Передаточные отношения планетарного редуктора:
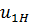 =
= 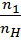 =
= 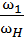 .
.
Передаточное отношение зубчатого ряда:
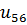 =
= 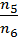 =
= 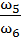 .
.
Общее передаточное отношение сложного зубчатого механизма:
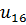 =
= 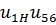 или
или 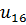 =
= 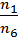 =
= 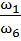 .
.
4. Находят относительную ошибку при определении результатов аналитическим и графическим методами по формулам:
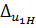 =
= 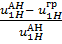 100%,
100%, 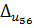 =
= 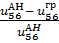 100%
100%
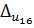 =
= 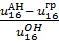 100%
100%
Ошибка вычислений не должна превышать 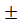 (5-7)%.
(5-7)%.
Дата добавления: 2015-02-13; просмотров: 1499;
