Основные задачи, решаемые способом вращения

Задача№1. Преобразовать прямую общего положения во фронтальную прямую уровня (рисунок 1.4.14).

Рассмотрим решение задачи, вращая прямую АВ вокруг горизонтально-проецирующей прямой i₁. Чтобы прямая АВ преобразовалась во фронтальную прямую уровня, необходимо ее повернуть вокруг оси, пока она не примет положение, параллельное фронтальной плоскости проекций. Если заданный отрезок прямой требуется повернуть до положения, параллельного плоскости П₁, то ось вращения следует расположить перпендикулярно П₂, если прямую следует повернуть до положения параллельного П₂, то ось вращения должна быть расположена перпендикулярно к плоскости П₁. Для упрощения графического решения этой задачи горизонтально проецирующую ось вращения i выберем проходящей через точку В. Тогда, при вращении прямой вокруг оси, точка В останется неподвижной (В₁≡В₁¹, В₂≡В₂¹), а точка А₁ примет положение А₁¹ и А₂¹. Траектория точки А является часть окружности а, лежащей в плоскости θ, параллельной П₁. Поэтому а₂≡θ₂, а₁ – окружность с центром в i₁, радиус которой равен отрезку А₁В₁. Преобразованная прямая будет являться фронтальной прямой уровня, а отрезок А₂В₂ – его натуральной величиной. Также в задаче определяется натуральная величина угла наклона φ прямой АВ к горизонтальной плоскости проекций.

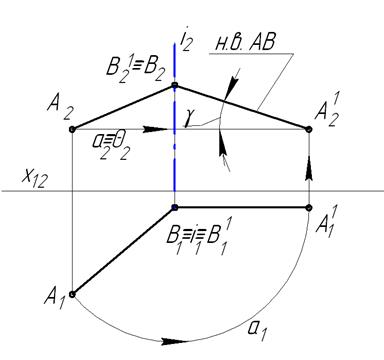
Рисунок 1.4.14 – Решение первой основной задачи способом вращения

Задача №2. Преобразовать прямую общего положения в горизонтально проецирующую прямую (Рисунок 1.4.15).

Эта задача решается при помощи двух преобразований: сначала прямую АВ преобразуем в прямую уровня (смотри задачу №1), а затем , чтобы прямая была перпендикулярно горизонтальной плоскости проекций, введем новую ось вращения i¹, перпендикулярную фронтальной плоскости проекций и проходящую через точку А. В этом случае точка А останется неподвижной, а точка В на чертеже примет положение В₂¹¹. Траектория точки В является часть окружности, лежащей в плоскости, параллельной фронтальной плоскости проекций, поэтому в горизонтальной плоскости проекций она совпадет с горизонтальной проекцией преобразованной прямой АВ (А₁¹В₁¹). Горизонтальная проекция прямой, после второго преобразования, будет являться точкой А₁¹¹В₁¹¹, т.е. прямая станет горизонтально проецирующей прямой.

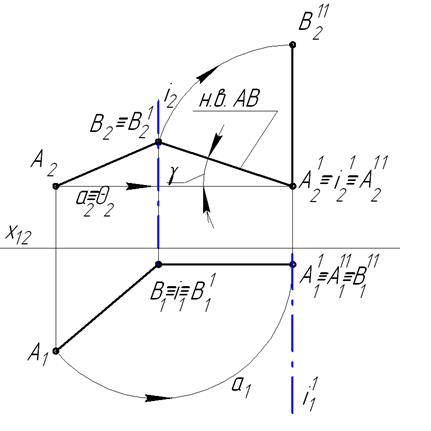
Рисунок 1.4.15 - Решение второй основной задачи способом вращения

Задача №3. Преобразовать плоскость общего положения во фронтально проецирующую (рисунок 1.4.16). Плоскость задана ΔABC.

Предварительно в плоскости проводим прямую уровня, в нашем случае – это горизонталь h. Заметим, если плоскость преобразуется в горизонтально проецирующую, то это – фронталь f. Через вершину В треугольника проведем горизонтально проецирующую ось вращения i и вокруг нее будем вращать треугольник до положения, перпендикулярного плоскости П₁. Для этого на чертеже поворачиваем фронтальную проекцию горизонтали h₁ вокруг горизонтальной проекцией оси вращения i₁ так, чтобы она по отношению к оси х располагалась перпендикулярно. При этом форма повернутой горизонтальной проекции треугольника A₁¹B₁¹C₁¹ осталась неизменной по отношению к проекции A₁B₁C₁. Так как горизонталь повернулась перпендикулярно фронтальной плоскости проекций, то на эту плоскость она проецируется в точку, а сам треугольник – в виде отрезка прямой A₂¹B₂¹C₂¹. Плоскость треугольника стала фронтально-проецирующей, а угол γ между фронтальной его проекцией и оси х – натуральной величиной угла наклона плоскости ΔABC к горизонтальной плоскости проекций.

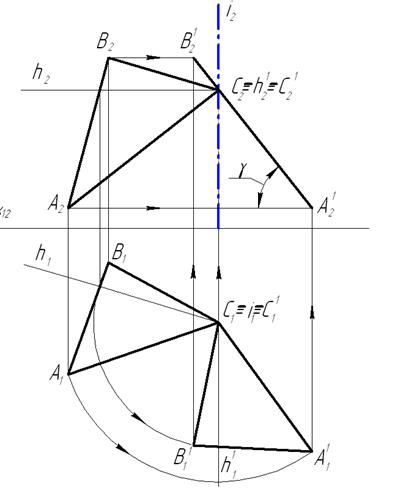
Рисунок 1.4.16 - Решение третьей основной задачи способом вращения

Задача №4. Преобразовать плоскость общего положения в горизонтальную плоскость уровня (рисунок 1.4.17).

Для решения этой задачи необходимо выполнить два преобразования (вращения): сначала повернуть плоскость, чтобы она стала фронтально проецирующей (смотри задачу №3), а затем, повернув вторично плоскость так, чтобы плоскость располагалась по отношению к горизонтальной плоскости проекций параллельно. Для второго вращения введем еще одну фронтально проецирующую ось вращения i¹, проходящую через точку А. На чертеже строим новую фронтальную проекцию ΔABC(A₂¹¹B₂¹¹C₂¹¹), повернутую вокруг i₂¹ до горизонтального положения. В горизонтальной проекции, в точках пересечения линий связи проекций одноименных точек треугольника, получим положение треугольника в горизонтальной плоскости уровня, а следовательно натуральную величину самого треугольника ABC.

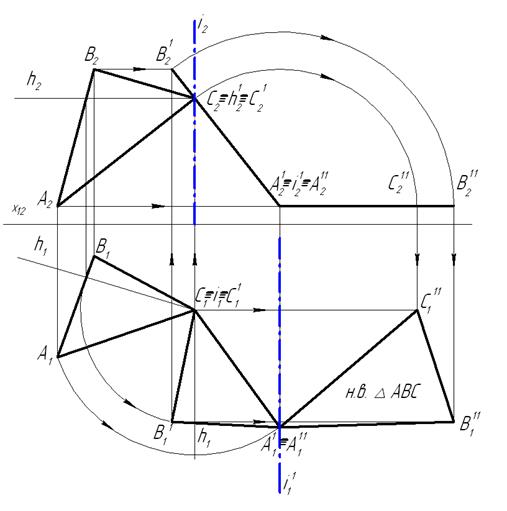
Рисунок 1.4.17 - Решение четвертой основной задачи способом вращения