Способ вращения вокруг проецирующей оси

При решении задач способом вращения положение заданных геометрических элементов изменяют путем вращения их вокруг некоторой оси.

Если ось вращения расположить перпендикулярно к плоскости проекций, то траектория вращения точки на эту плоскость проецируется окружностью, а угол поворота точки будет проецироваться в натуральную величину.

На рисунке 1.4.13 данная точка А повернута вокруг горизонтально проецирующей оси i на угол φ. Для этого:

1) Через точку А проведена плоскость вращения Ρ_┴i;

2) Центром вращения будет являться точка пересечения плоскости Ρ с осью i (Ρ∩i=C);

3) Окружность, описываемая точкой А и имеющая радиус R=AC, проецируется на горизонтальную плоскость проекций в натуральную величину, а на плоскость П₂ в виде отрезка прямой, перпендикулярной к соответствующей проекции оси вращения – i₂.

4) При повороте точки А на угол φ до положения А¹, горизонтальная проекция точки А₁ будет перемещаться по окружности, а фронтальная А₂ – по прямой, параллельной оси х.

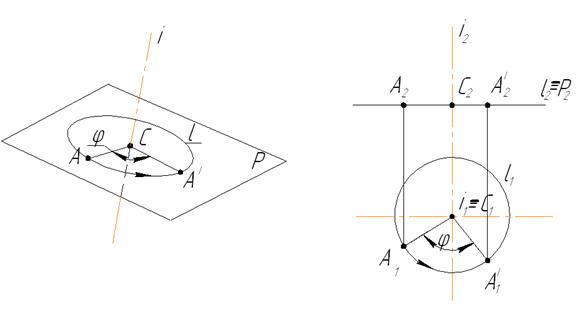
Рисунок 1.4.13 – Вращение точки вокруг проецирующей оси