Поверхности вращения
Поверхностью вращения называется поверхность, которая описывается какой-либо образующей при её вращении вокруг неподвижной оси.
Образующая может быть как плоской, так и пространственной кривой. В частном случае это может быть прямая линия. Для задания поверхности вращения необходимо задать её ось i и какую-либо образующую l, лежащую на этой поверхности. Определитель поверхности вращения: Г(i, l). На чертеже она может быть задана проекциями этих элементов в соответствии с рисунком 1.3.40. Каждая точка L кривой l описывает при вращении окружность m с центром на оси i. Эти окружности называются параллелями поверхности. Кривые q, получающиеся в сечении поверхности вращения плоскостями Q(Q1), проходящими через ось i, называются меридианами.
Поверхность симметрична относительно любой меридиональной плоскости, а все меридианы равны между собой. В соответствии с рисунком 1.3.40 образующая l лежит на одном из меридианов.
Если поверхность вращения расположить так, чтобы её ось i была перпендикулярна к плоскости проекций П1, то все параллели спроецируются на эту плоскость без искажения. Меридиан q, расположенный во фронтальной плоскости Q (Q1), называется главным меридианом. Он проецируется без искажения на плоскость проекций П2 и определяет очертаниеповерхности на этой плоскости. Для построения очертания поверхности надо вращать точки образующей кривой l до их совпадения с плоскостью главного меридиана Q. В соответствии с рисунком 1.3.40 получена точка L, принадлежащая главному меридиану и, соответственно, очертанию поверхности. Именно таким образом строится очертание поверхности вращения по её определителю: в плоскость главного меридиана выводится определённое количество точек, соединяемых затем плавной кривой линией.
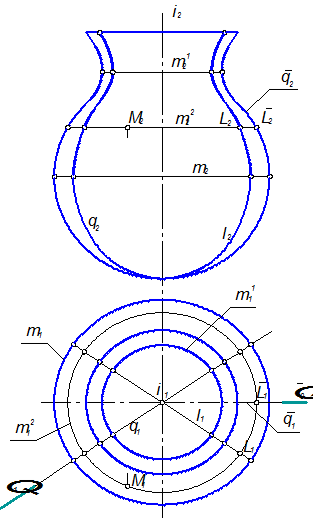
Рисунок 1.3.40 – Поверхность вращения
Параллели наибольшего и наименьшего радиусов называются соответственно экватором и горлом поверхности вращения. Они проецируются на плоскость П1 в виде окружностей очертания. В соответствии с рисунком 1.3.40 это окружности m и m’.
Для построения точек, принадлежащих поверхности, можно использовать линии каркаса поверхности. Каркас поверхности вращения удобнее всего составлять из меридианов или параллелей, или из тех и других. Например, для нахождения второй проекции точки М(М2), взятой на поверхности в соответствии с рисунком 1.3.40 следует провести через М2 параллель m(m2) и найти её горизонтальную проекцию m1, на которой и будет находиться горизонтальная проекция М1 точки М.
Дата добавления: 2015-02-13; просмотров: 743;
