Движение границы раздела двух жидкостей в пористой среде. Поршневое вытеснение водой в залежах полосообразной и круговой форм.

Строгое гидродинамическое решение задачи о движении границы раздела двух жидкостей в общем случае отсутствует. Оно существует для прямолинейного и плоскорадиального притоков. Эти задачи возникли в связи с вопросом о стягивании контура нефтеносности или газоносности при водонапорном режиме течения в процессе разработки нефтяной или газовой залежи.

Полагаем, что вытеснение происходит «поршневым» образом, т.е. считаем границу раздела некоторой поверхностью.

Рассмотрим прямолинейное движение контура нефтеносности (КН) к прямолинейной батарее скважин в полосообразном пласте.

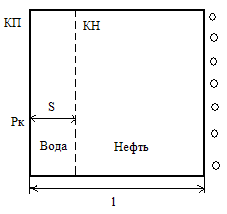
Рис. 16.1 – Схема прямолинейного движения границы раздела 2-х жидкостей

Принимаем: Рк=const – давление на КП; Рс=const – давление на одной из близких изобар к батарее скважин; ω(s)=const. Для определения времени продвижения воспользуемся формулой(1):

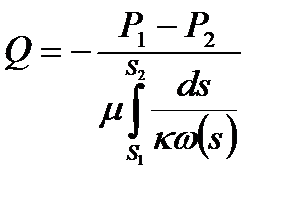(16.1)

При t₀=0, имеем:

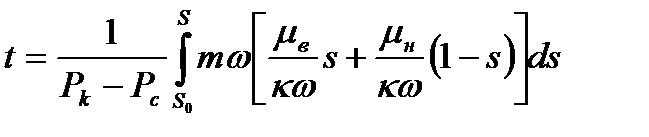(16.2)

После интегрирования получаем:

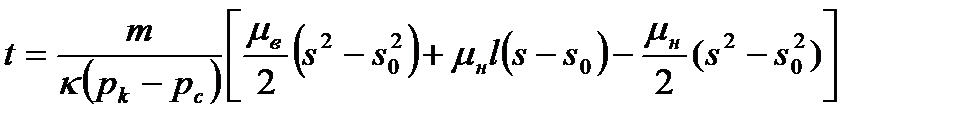
или

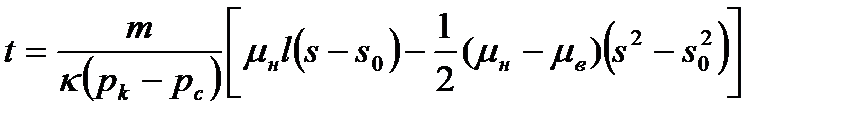(16.3)

Для одножидкостной системы (μ_н=μ_в=μ),из Ур-ия (16.3) следует:

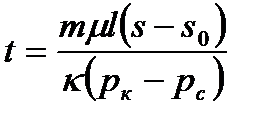(16.4)

Формула (16.4) получается также элементарным путем. Если за время t пройден путь S - S₀, а истинная скорость движения u=const и равна:

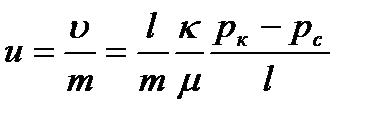(16.5)

то

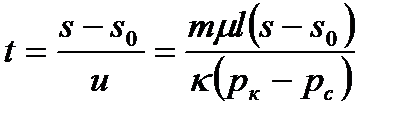(16.6)

При S=l (смотри рис.) получим время вытеснения водой.

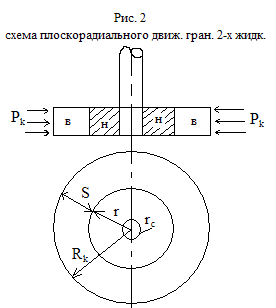
Плоскорадиальное движение границы раздела с постоянной толщиной, пористостью и проницаемостью.

Рассмотрим плоскорадиальное движение кругового контура нефтеносности к совершенной скважине при установившемся процессе фильтрации по линейному закону Дарси. (рис. 16.2). Контур питания представляет собой окружность радиуса R_k, где давление Р_к=const. На контуре скважины радиуса r_c поддерживается давление Р_с=const. По условию: h=const, m=const, k=const.

В данном случае площадь фильтрации ω(s)=2πrh является переменной величиной. Так как S=R_k - r (рис.16.2), то ds= - dr.

Имеем:

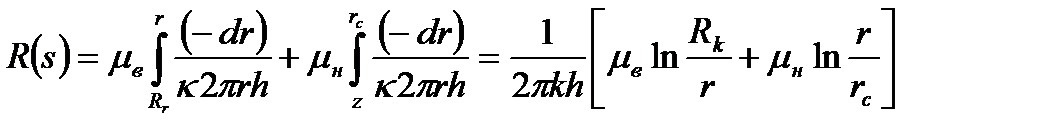(16.7)

Подставляя значение (16.7) в:

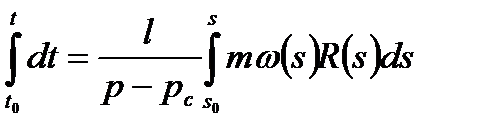
Интегрируя в пределах от начального положения радиуса контура нефтеносности r₁ до его конечного положения r₂, при t=0 получим

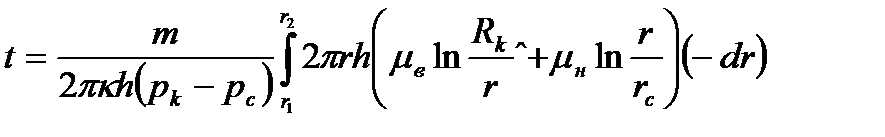
После интегрирования и преобразований получаем:

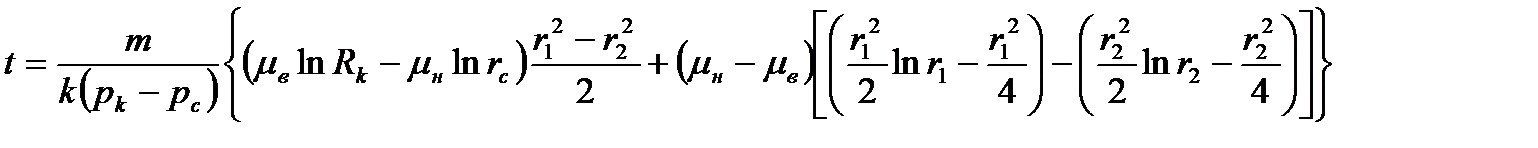(16.8)

Время прорыва воды в скважину определится из (16.8) при r₂=r_c.