INPUT A,B,C,D,H
YMAX=-1E-10
for x =A to B step H
у=x* sin(c* x +d)
if у>YMAX then YMAX =у
next x
print YMAX
end
Пример 5. Составить программу для нахождения наименьшего элемента массива Х(50) и его порядкового номера.
option base 1
dim X(50)
for i=1 to 50
input X(i)
next i
XMIN =X(1)
for i=2 to 50
if X(i)<XMIN then XMIN=X(i) : k= i
next i
print k, XMIN
end
Простейшие алгоритмы обработки массивов.
Элементы массивов могут быть использованы для вычислений только после того, как их значения будут записаны в память ЭВМ. Простейшим способом ввода является последовательная запись вводимых элементов с помощью операторов READ-DATA. Например,
dim C(3)
READ C(0), C(1), C(2),C(3)
DATA 3.,4.86,3E-5,-1.22
В данном фрагменте программы осуществляется ввод четырёх элементов массива С. Данный способ, естественно, применим только для ввода небольшого количества элементов.
Более употребительным является ввод массива, реализованный с помощью циклического вычислительного процесса. Например,
а) DIM A(9)
for i=0 to 9
read A(i)
next
DATA 1.,2.,3.,4.,5.
DATA 6.,7.,8.,9.,10.
б) DIM(9)
for i=0 to 9
input A(i)
next
Ввод элементов двумерного массива обычно осуществляется по строкам. Например, с помощью операторов
а) DIM S(3,2)
for i=0 to 3
for j=0 to 2
read S(i, j)
next j
next i
DATA 1.,2.,3.,4.,5.,6.
DATA 7.,8.,9.,10.,11.,12.
б) DIM S(3,2)
for i=0 to 3
for j=0 to2
input S(i, j)
next j
next i
задаем массив
| 1 2 3 |
| 4 5 6 |
| 7 8 9 |
| 10 11 12 |
При большом количестве элементов в массиве удобно при использовании оператора INPUT пользоваться такой последовательностью операторов
DIM S(3,2)
for i=0 to 3
INPUT S(i,0),S(i,1),S(i,2)
next i
При этом на каждый знак вопроса печатаются через запятую и вводятся все элементы соответствующей строки.
Вывод массивов может осуществляться такими же последовательностями операторов печати PRINT.
Рассмотрим в качестве примера вывод на печать (по строкам) двумерного массива.
for i=1 to n
for j=1 to k
PRINT A(i, j)
next j
next i
Наглядность вывода может быть нарушена, если элементы массива А представляется различным числом значащих цифр. В этом случае можно предложить:
а) использование зонного формата, поставив запятую в строке с оператором PRINT вместо точки с запятой;
б) использование оператора PRINT USING.
При решении многих практических задач могут производиться различные операции над массивами. Рассмотрим примеры таких задач.
Задача 1. Сортировка элементов массива.
Выполнить сортировку элементов какого-нибудь множества – это значит упорядочить их по выбранному признаку. Число можно сортировать по величине, детали –по весу, список авторов составляется в порядке алфавита. Задача сортировки- одна из практически важных, и поэтому математики и программисты потратили немало усилий для отыскания эффективных алгоритмов её решения. Приведём пример простейшей программы сортировки чисел по их величине. В этой программе используется стандартная функция
SWAR A,B
которая меняет между собой значения двух переменных А и В одного и того же типа, что невозможно выполнить двумя последовательными операторами присваивания (А=В: В=А).
Сортировка элементов массива
INPUT N
OPTION BASE 1
DIM A(N)
for i=1 to N.
INPUT A(I)
next i
PRINT "Укажите принцип сортировки"
PRINT "По возрастанию элементов? Да или Нет"
INPUT K$
if K$="Да'' then m1
for i=1 to N-1
for j=1+i to N
if A(i)<A(j) then m2
goto m3
m2:
SWAR A(i),A(j)
m3:
next j
next i
goto m4
m1:
for i=1 to N-1
for j=1+1 to N
if A(I)>=A(J) then m5
goto m6
m5:
SWAR A(I),A(J)
m6:
next j
next i
m4:
PRINT "Печать отсортированного массива"
for k=1 to N
print A(k);
next k
end
Задача 2. Вычисление площади многоугольника.
Если координаты вершин n-угольника равны (X i, Y i), где i=0,1,…n, то площадь многоугольника может быть вычислена по формуле
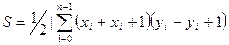
где (X0,Y0)=(X n, Y n). В программе используются переменные: N- количество вершин многоугольника; S- его площадь; X i, Y i- координаты вершин.
Площадь многоугольника.
INPUT "Количество вершин N=";N
DIM X(N), Y(N)
Print "Введите координаты(x,у) вершин"
for i=1 to N
INPUT X(i), Y(i)
next i
X(0)=X(N): Y(0)=Y(N): S=0
for i=0 to N-1
S=S+(X(i)+X(i+1))*(Y(i)-Y(i+1))
next
S=ABS(S)/2
Print "ПлощадьS="; S
end
Задача 3. Перестановка строк матрицы.
Пусть в матрице А(n, m) необходимо выполнить перестановку i-й и j-й строк. Запишем лишь фрагмент программы.
for k=1 to m
SWAR A(i, k), A(j, k)
next k
Задача 4. Преобразование матрицы в одномерный массив.
Требуется переслать элементы матрицы А(n, m) в одномерный массив Х того же размера с сохранением порядка следования по строкам.
Приведём фрагмент программы.
for i=1 to n
for j=1 to m
X((i-1)*m+ j)=A(i, j)
next j
next i
Задача 5. Поиск минимального элемента матрицы А(N,M).
Приведем лишь фрагмент программы.
P=A(1,1): k=1: L=1
for i=1 to n
for j=1 to m
if P>=A(i, j) goto m1
P=A(i, j): k= i: L= j
m1:
next j
next i
Подпрограммы и процедуры
Подпрограмма- это группа операторов или часть программы, описывающая некоторый алгоритм, который можно многократно использовать, обращаясь к нему из различных точек программы. Подпрограммы снимают те ограничения, которые имеют функции пользователя:
а) они состоят из одного оператора,
б) с их помощью можно вычислять только одно значение,
в) ими можно пользоваться только в той программе, в которой они определены.
С программами, не подозревая об этом, мы часто сталкивались в программах, записывая обращения к стандартным функциям (sin, abs, exp и т. д.). Каждая из них представляет собой небольшую программу, точнее, подпрограмму, поскольку имеет подчиненную роль в процессе счета. Обнаружив в операторе имя стандартной функции, ЭВМ вычисляет её аргумент (фактический параметр) и с этим значением переходит из программы на блок вычисления значения функции, запомнив при этом место возврата.
Для обращения к подпрограмме используют оператор
GOSUB m1
где GOSUB (перейти к программе)- имя оператора; m1- метка первого оператора подпрограммы. Любая подпрограмма должна завершаться специальным оператором возврата
RETURN
После выполнения подпрограммы оператор RETURN возвращает управление оператору, следующему за оператором GOSUB
Подпрограмма может располагаться в любом месте программы, однако удобнее размещать её в конце программы перед оператором END. Например, для вычисления корней двух квадратных уравнений вида Ах^2+Вх+0=0 может быть записана следующая программа
DATA 1.4,5.2,0.77,2.6,4.8,1.1
READ A,B,C
GOSUB m1
READ A,B,C
GOSUB m1
STOP
m1:
D=B*B-4*A*C
IF D<0 THEM PRINT "Корней нет": GOTO m3
X1=(-B+SQR(D))/(2*A)
X2=(-B-SQR(D))/(2*A)
PRINT "X1=";"X2=";X2
m3:
RETURN
END
Следует обратить внимание, что если бы в программе отсутствовал оператор STOP, то подпрограмма выполнялась бы и в третий раз, но при попытке выхода из неё произошла бы ошибка, т. к. переход на подпрограмму был осуществлен не оператором GOSUB.
Подпрограммы могут содержать обращения к другим подпрограммам. Пусть, например, требуется считать данные, подставить их в разные формулы и напечатать полученные результаты. Вычисления по формулам и печать результатов оформим как подпрограммы.
DATA 2, 4
READ A, B
GOSUB m1
STOP
m1:
X=A: Y=B
GOBUS m2
X=X^2: Y=Y^2
GOBUS m2
X=X+1/A: Y=Y-1/A
m2:
PRINT X,Y
RETURN
END
Заметим, что здесь один оператор RETURN обслуживает три оператора GOSUB. Результатом работы этой программы является следующая информация:
2 4
4 16
4,5 15,5
При использовании подпрограммы необходимо заботиться о присвоении необходимых значений входным параметром подпрограммы и о сохранении результатов её выполнения, иначе они будут испорчены при повторных обращениях к ней.
Процедурами называются части программы, ограниченные операторами SUB и END SUB. Существует формальный синтаксис объявления процедуры:
SUB имя процедуры [список параметров]
[объявление переменных]
операторы
процедуры
Дата добавления: 2015-02-10; просмотров: 1061;
