Класс InputStream
1. В меню Processing выберите Simulation Tool. Выполните настройки, как показано ниже на рис.2.18.
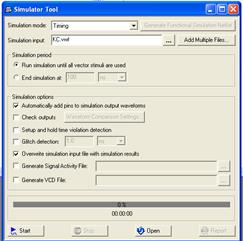
Рис.2.18.
2. Нажмите кнопку Start и запустите моделирование. При появлении сообщения об успешном окончании процесса моделирования нажмите кнопку OK.
3. Откройте окно KC.vwf, в которое в соответствии с выполненными настройками симулятора перепишутся результаты моделирования, и проанализируйте результаты моделирования. Результаты моделирования также доступны, если нажать иконку  , находящуюся на панели инструментов менеджера пакета. Симулятор в соответствии с функционально-логическим описанием, полученным в результате компиляции введенной схемы, задержками, вычисленными после размещения и разводки, и заданным при вводе временной диаграммы тестовым воздействием на входах, вычисляет реакцию на выходе Y. Результаты моделирования, представленные на рис.2.19 соответствуют таблице истинности, для которой синтезировалась схема примера.
, находящуюся на панели инструментов менеджера пакета. Симулятор в соответствии с функционально-логическим описанием, полученным в результате компиляции введенной схемы, задержками, вычисленными после размещения и разводки, и заданным при вводе временной диаграммы тестовым воздействием на входах, вычисляет реакцию на выходе Y. Результаты моделирования, представленные на рис.2.19 соответствуют таблице истинности, для которой синтезировалась схема примера.
 |
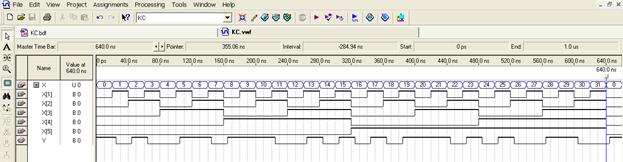
Рис.2.19.
1.3. Риск сбоя в комбинационной схеме
Модели реальных логических элементов, на которых реализуется комбинационная схема, отличаются от идеальных элементов наличием задержки сигнала, как показано на рис. 2.20.
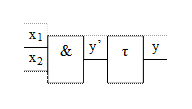
Рис.2.20. Модель реального логического элемента с учетом задержки.
Появление задержки приводит к тому, что на коротком промежутке времени не реализуются логические функции, описывающие работу идеальных ЛЭ. Так в схеме на рис. 2.20 при х2=1 и переключении х1 из состояния 1 в состояние 0 в течение времени, определяемом задержкой переключения, будет реализовано х2=1, х1=0, y=1, что противоречит логической функции, реализуемой элементом.
Задержка сигнала t различна для различных серий логических элементов и составляет, например, порядка 15 нс. для серии К155 и 3 нс для серии К1554. В микросхемах программируемой логики задержки зависят от размещения и разводки проекта, выполненных модулем Fitter. Для СБИС ПЛ Cyclone II задержки около 10 нс. (См. отчет временного анализатора). Сигналы в комбинационных сетях проходят пути от входов к выходу, состоящие из различного числа логических элементов и, значит, имеющие различные задержки сигналов, определяемые как сумма задержек логических элементов и соединительных линий, входящих в путь. Если между каким-либо входом и выходом комбинационной схемы имеется несколько путей прохождения сигнала (два и больше), то при переключении сигнала на этом входе происходит состязание сигналов на различных путях, которое может привести к появлению на выходе комбинационной схемы неалгоритмических переходов, так называемых рисков сбоя.
Статический риск сбоя нуля представляет собой короткий единичный импульс, возникающий при смене комбинаций входных переменных, дающих нулевое значение функции. Статический риск сбоя единицы – короткий сигнал нулевого уровня, возникающий при смене комбинаций входных переменных, дающих единичное значение функции.
Длительность импульсов риска сбоя определяется разностью в задержках прохождения сигналов по различным путям и не превышает, как правило, десятков наносекунд.
Для борьбы с рисками сбоев используются следующие приемы:
· введение синхронизации, т.е. считывание выходного сигнала после окончания переходных процессов в комбинационной схеме;
· разработка комбинационных схем, в которых исключены неалгоритмические переходы;
· использование импульсных фильтров на выходе комбинационной схемы для задерживания коротких сигналов риска сбоя (например, могут использоваться формирующие свойства цепочки логических элементов);
· введение ограничений на последовательность изменения аргументов таким образом, чтобы исключить комбинации, на которых возможны риски сбоя.
Наиболее часто используются два первых способа борьбы с рисками сбоев. Рассмотрим подробнее вопросы проектирования комбинационных схем, свободных от статических рисков сбоя.
Аналитические методы анализа состязаний предусматривают задание функций в ДНФ при анализе статических рисков сбоя нуля и в КНФ при анализе статических рисков сбоя единицы с дальнейшим рассмотрением прямого и инверсного значений аргументов, как разных переменных, и выявлением условий, при которых нарушаются значения истинности ЛФ.
Использование карт Карно позволяет не только проанализировать ситуации, приводящие к возникновению статических рисков сбоя, но и синтезировать комбинационную схему без статических состязаний сигналов для ЛФ приемлемой размерности. При минимизации прямого значения логической функции (склеивании единиц) могут возникать только статические риски сбоя единицы при изменении значения какого-либо аргумента, приводящем к переходу в карте Карно между единицами, не связанными общим контуром склеивания. Для устранения риска сбоя при таком переключении необходимо ввести дополнительный контур склеивания, охватывающий соответствующие единицы, т.е. усложнить комбинационную схему. При склейках нулей могут возникать только статические риски сбоя нуля, борьба с которыми может вестись также введением дополнительных склеек.
В рассмотренном примере синтеза (см. рис.2.4 ) риски сбоя могут возникать по переменной х1 при наборе аргументов x5432=0100 (переход между контурами склеивания 1 и 6) и по переменной х4 при наборе аргументов x5321=1111 (переход между контурами склеивания 6 и 7). Для создания КС свободной от состязаний потребовалось бы дополнить полученную минимальную ДНФ еще двумя слагаемыми, склеивающими единицы на наборах 8, 9 и 17, 25.
1.4. Проверка и наладка реализуемой схемы
Проверку реализуемой КС осуществляют, заполняя на основе экспериментального исследования схемы (на имитационной и физической моделях) графу yэксп. таблицы истинности и сравнивая значения yэксп. и yтеор. Для получения экспериментальных значений yэксп. удобно подавать на входы КС наборы аргументов, соответствующие последовательно нарастающим значениям пятиразрядного двоичного кода, в том числе и коды, соответствующие комбинациям аргументов, на которых ЛФ не определена (в таблице истинности отмечено, как эти значения доопределены в процессе минимизации ЛФ). Если экспериментальные и теоретические значения y совпали – КС реализует заданную функцию. Если хотя бы на одном наборе аргументов нет совпадения, необходимо осуществить наладку собранной схемы.
Наладка КС производится на основе анализа полученных значений yэксп и сравнения их с yтеор. ЛФ может не реализовываться из-за ошибок в синтезе и/или из-за ошибок реализации на физической модели. Вначале следует проверить синтезированную КС имитационным моделированием средствами Quartus II. Если результаты исследования модели положительны, можно переходить к реализации физической модели на макете DiLaB. Если экспериментальные результаты не совпали с заданной таблицей истинности, необходимо проверить ввод схемы и ее синтез.
Однако выявление ошибки синтеза полными повторными расчетами трудоемко и в результате не всегда позволяет оперативно выявить ошибку. Поэтому целесообразно локализовать нереализуемую часть ЛФ, используя снятую экспериментальную таблицу истинности. Для этого на карте Карно отмечаются нереализуемые единицы и в минимальной ДНФ, полученной в процессе минимизации, ищутся склейки, обеспечивающие появление этих единиц. Производится контроль заполнения карты Карно и дальнейших преобразований только для нереализуемых склеек. Если проверка не выявила ошибки в синтезе, то следует искать дефект в технической реализации КС; если ошибка синтеза найдена, необходимо внести исправления в схему и снова снять экспериментальную таблицу истинности.
Для получения дополнительной информации о работе схемы при настройке можно показать на временной диаграмме значения промежуточных сигналов в комбинационной схеме. Исходно для отображения доступны только входы/выходы микросхемы и выходы триггеров. Для получения доступа к внутренним сигналам КС их следует подключить к примитивам вывода output, а для того, чтобы эти выходы не занимали выводы микросхемы, назначить их как виртуальные (без физической привязки) выводы. Для этого щелкните правой кнопкой по символу выхода и в появившемся окне выберите Locate => Locate in Assignment Editor. В появившемся окне ( Рис.2.21) выполните назначение Virtual Pin.
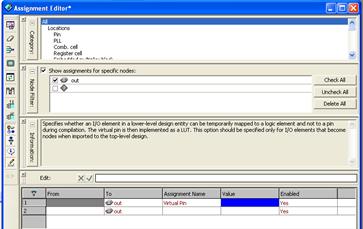
Рис.2.21.
1.5. Реализация комбинационной схемы на физической модели
Для реализации комбинационного устройства на макете DiLaB выполните назначения входов КС на выводы СБИС ПЛ подключенные к выбранным переключателям SW[8..1], а выход подключите к выбранному для индикации светодиоду (светодиодам). Разводка выводов и назначение описаны во вводной работе.
Выполните компиляцию проекта и, открыв окно программатора, нажмите на кнопку Start. Получив сообщение об успешном окончании программирования, приступите к проверке работы КС на физической модели.
При отладке физической модели все дефекты синтеза КС уже устранены по результатам моделирования в среде Quartus II. Неправильная работа КС может быть вызвана только дефектами реализации физической модели, например, не соответствием переменных и кнопок управления, неисправностью стенда и т.п.
Процедуру наладки реализуемой КС повторяйте до тех пор, пока не будет достигнуто соответствие теоретической и экспериментальной таблиц на всех наборах аргументов, что говорит о правильной реализации заданной ЛФ.
1.6. Программа работы
1. Запишите заданную списком ЛФ пяти переменных в виде таблицы истинности, предусмотрев в таблице графы yтеор для записи доопределенной в процессе синтеза ЛФ и yэксп. для занесения результатов экспериментальных исследований на имитационной и физической моделях.
2. Постройте карту Карно.
3. Осуществите минимизацию ЛФ для реализации в базисе Шеффера и выберите один из минимальных вариантов. Запишите логическое выражение, соответствующее минимальной ДНФ ЛФ.
4. Для реализации ЛФ в базисе 2И-НЕ, 3И-НЕ, 4И-НЕ осуществите факторизацию полученного логического выражения и запишите ЛФ в базисе Шеффера с ограничениями.
5. Создайте описание КС в САПР Quartus II, используя средства графического ввода.
6. Выполните компиляцию КС. В файле отчета временного анализатора найдите и запишите задержки сигналов по всем входам.
7. В редакторе временных диаграмм САПР Quartus II создайте тест, в котором работа КС проверяется на всех наборах входных сигналов.
8. Выполните моделирование КС в САПР Quartus II. Убедитесь, что КС формирует значения выходного сигнала, соответствующие заданию, на всех наборах. Отличие результатов для хотя бы одного набора является ошибкой.
9. Проверьте состязания сигналов по указанному преподавателем аргументу. Приведите временные диаграммы, оцените длительность импульса при неалгоритмическом переходе, предложите способ устранения риска сбоя.
10. Реализуйте КС на физической модели, как описано в п. 1.5.
11. Проверьте значения ЛФ на всех наборах аргументов, занося результаты эксперимента в таблицу истинности. При необходимости осуществите наладку схемы, указывая в отчете принимаемые на каждой итерации наладки меры и экспериментальные результаты.
12. Оформите и сдайте отчет по работе.
1.7. Контрольные вопросы
1. Укажите способы задания ЛФ.
2. Приведите примеры функционально полных базисов.
3. Какая функция считается не полностью определенной?
4. В чем заключается минимизация ЛФ?
5. Как доопределить не полностью определенную ЛФ?
6. Каким образом можно перейти от записи логического выражения в ДНФ к базису Шеффера?
7. Как на двухвходовых ЛЭ И-НЕ реализовать логическое произведение четырех аргументов?
8. Как влияет ограничение числа входов используемых ЛЭ на быстродействие синтезируемой КС?
9. Определите быстродействие разработанной КС. Каким образом можно повысить быстродействие?
10. Укажите примеры возникновения риска сбоя в разработанной КС. Предложите способы устранения.
11. Что такое Virtual Pin?
1.8. Варианты заданий по синтезу КС
| Номер | Значения наборов аргументов | |
| задания | Для значений y=1 | Для значений y=н |
| Пример | 0,2,5,6,8-10,13,15,17,19-21,25,28 | 12,23,29,30 |
| 0,2,6,9,14,16,20,21,25-29 | 1,13,17,19,30 | |
| 3-8,11,13,15,20,22-25,30,31 | 2,12,19,26,27 | |
| 0-2,5,8,9,11-14,19-21,24,26,29,30 | 6,16,23,28 | |
| 0,2,4,7-10,13,15,18-20,22,23,27-30 | 11,17,24,31 | |
| 3-5,7,9,13,15,18,20-22,26-28,30,31 | 8,10,12,16 | |
| 1,12,13,14-17,21,24-26,28 | 8-11,30 | |
| 3,4-7,9-11,18,21-28 | 1,15,17,31 | |
| 1,6-10,13,15,20-25,28,31 | 3,4,12,17,26 | |
| 0,1,4,7,10,12,14,19,20,23,24,26-29 | 2,15,22,25 | |
| 3,6,8-11,14,16,19-23,27,28 | 0,12,13,30,31 | |
| 1,5-9,12,13,17,20-25 | 2,16,28,30,31 | |
| 0,4-7,9,13,15-20,25-30 | 2,14,22,23,31 | |
| 6-10,13,15,17,21-26,30 | 0-2,18,20,31 | |
| 0,2,4,6,7,9-12,17-20,23,25,27-29 | 13-16,22,30 | |
| 0,2,4,6,9-13,18,21-25,26,27,29,31 | 1,7,15,20,28 | |
| 1,3-6,10-14,17,19,23-27,31 | 0,8,21,30 | |
| 2,4-7,11-15,18,23-27,30 | 0,10,17,20 | |
| 5-8,10,12,15-17,20-24,29-31 | 0,3,13,27 | |
| 5-12,14,16,18,21,24-28 | 0-2,17,31 | |
| 0,2,4,6,7,9,11,14,16,18,22,24,25,27 | 12,13,19,30 | |
| 1,3,4,5,9,11,13,14,16-18,20,22 | 2,6,21,28 | |
| 2,5-7,9,10,13-15,16,18,20-23 | 0,8,28,30,31 | |
| 0,1,5,9-14,18,21-23,26 | 6,16,17,29 | |
| 2,4,9-11,13-15,18,22,25,27-29 | 1,17,20,21,24 | |
| 1,3-5,10,14,15,17,19,21,23,24-28 | 8,11,13,22 |
Класс InputStream
В абстрактном классе InputStream объявляются методы для чтения из заданного источника. InputStream является базовым классом для большинства входных потоков в java.io и содержит следующие методы, которые (кроме конструктора) при обнаружении ошибки во входном потоке возбуждают исключение IOException:
· public InputStream()
Класс InputStream содержит только безаргументный конструктор.
· public abstract int read() throws IOException
Читает из потока один байт данных и возвращает прочитанное значение, лежащее в диапазоне от 0 до 255 (не от –128 до 127). При достижении конца потока возвращается флаг –1. Метод блокирует работу программы до появления значения на входе.
· public int read(byte[] buf)
Читает данные в массив байтов. Метод блокирует работу программы до появления вводимого значения, после чего заполняет buf всеми прочитанными байтами, в количестве не более buf.length. Метод возвращает фактическое количество прочитанных байтов или –1 при достижении конца потока.
· public int read(byte[] buf, int off, int len)
Читает данные в байтовый подмассив. Метод блокирует работу программы до начала ввода, после чего заполняет часть массива buf, начиная со смещения off, в количестве до len байтов, если не встретится конец массива buf.
· public long skip(long count)
Пропускает до count байтов во входном потоке. Количество пропущенных байтов может быть меньше count из-за достижения конца потока. Возвращает фактическое количество пропущенных байтов.
· public int available()
Возвращает количество байтов, которые могут быть прочитаны без блокировки работы программы.
· public void close()
Закрывает входной поток. Метод должен вызываться для освобождения любых ресурсов (например, файловых дескрипторов), связанных с потоком. Если не сделать это, то ресурсы будут считаться занятыми, пока сборщик мусора не вызовет метод finalize данного потока.
Дата добавления: 2015-02-16; просмотров: 830;
