Критерий оптимальности последовательности включения агрегатов станции.
Оптимальность последовательности включения агрегатов эл.станций обуславливается наивыгоднейшим распределением нагрузки между ними. Использование метода множителей Лагранжа позволяет получить условие наивыгоднейшего распределения нагрузки между агрегатами эл/ст. в виде равенств отношений приростов расхода первичного ресурса (приведенной мощности) к приращению вторичного ресурса (полезной мощности) при соблюдении балансовых ограничений.
1)М/у агрегатами ТЭС:
а) м/у турбинами
б) м/у котлами
в) м/у блоками
bT,I – относительный прирост турбины
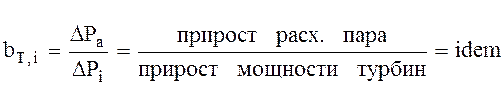
bk,I - относительный прирост котлов
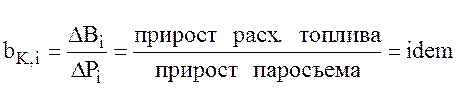
bБ,I – относительный прирост блока блок=котел+турбина
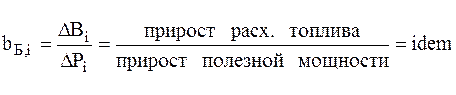
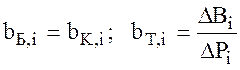bT,i = idem (i)
На эти уравнения накладываются ограничения, т.к. характеристики имеют скачки и участки постоянного прироста.
турб.1 турб.2
dT
dT Р1>P2
P P
Pmin1 P1 Pmax1 Pmin2 P2 Pmax2
Pmin=Pmin1+Pmin2
1. Pmin<P<Pmin+P2 – загрузка агр.2
2. Pmin+P2<P<P1+P2 – загрузка агр.2
3. P1+P2<P<P1+Pmax2 – загрузка агр.2
4. P>P1+Pmax2 – загрузка агр.1
При такой методике всегда используется агрегат с наибольшей экономией топлива. Если агрегаты не имеют равных относительных приростов, то они загружаются в порядке возрастания их относительных приростов.
2) Распределение нагрузки м/у агрегатами ГЭС
Распределение нагрузки м/у агрегатами ГЭС является наивыгоднейшим, если они работают с одинаковыми относительными приростами.
Задача наивыгоднейшего распределения нагрузки м/у агрегатами станций проста, если известны характеристики относительных приростов. Но в условиях эксплуатации желательно использовать не характеристики, а измерение относительных приростов.
Для этого с малым шагом дискретности измеряем а1 и а2 и соответствующие им Р1 и Р2.
Дата добавления: 2015-02-10; просмотров: 1145;