Трехфазное короткое замыкание в неразветвленной цепи
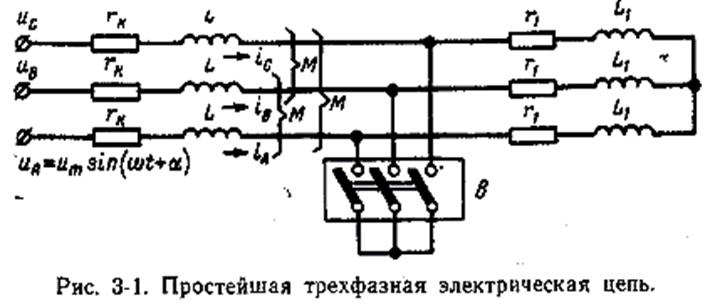
Обратимся к рис. 3-1, на котором представлена простейшая симметричная трехфазная цепь. В ней условно принято, что на одном ее участке имеется взаимоиндукция между фазами, а на другом она отсутствует. Цепь присоединена к источнику синусоидального напряжения с неизменными амплитудой и частотой.
Рассмотрим переходный процесс, вызванный включением выключателя В, за которым сделана закоротка, что равносильно возникновению металлического трехфазного короткого замыкания между двумя участками данной цепи.
Пусть векторы 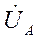 ,
, 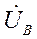 ,
, 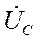 ,
, 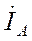 ,
, 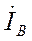 ,
, 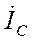 (рис. 3-2) характеризуют предшествующий режим рассматриваемой цепи, а вертикаль tt является неподвижной линией времени, т. е. мгновенные значения отдельных величин определяются проекциями на эту линию соответствующих вращающихся векторов. Момент возникновения короткого замыкания будем фиксировать значением угла а (т. е. фазой включения) между вектором напряжения фазы А и горизонталью (рис. 3-2).
(рис. 3-2) характеризуют предшествующий режим рассматриваемой цепи, а вертикаль tt является неподвижной линией времени, т. е. мгновенные значения отдельных величин определяются проекциями на эту линию соответствующих вращающихся векторов. Момент возникновения короткого замыкания будем фиксировать значением угла а (т. е. фазой включения) между вектором напряжения фазы А и горизонталью (рис. 3-2).
После включения выключателя В цепь рис. 3-1 распадается на два независимых друг от друга участка. Участок с 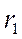 и
и 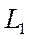 оказывается зашуитированным коротким замыканием и ток в нем будет поддерживаться лишь до тех пор, пока запасенная в индуктивности
оказывается зашуитированным коротким замыканием и ток в нем будет поддерживаться лишь до тех пор, пока запасенная в индуктивности 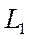 энергия магнитного потока не перейдет в тепло, поглощаемое активным сопротивлением
энергия магнитного потока не перейдет в тепло, поглощаемое активным сопротивлением 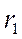 .
.
Дифференциальное уравнение равновесия в каждой фазе этого участка имеет вид:
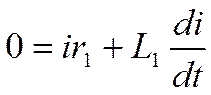 . (3-1)
. (3-1)
Его решение общеизвестно:
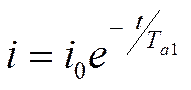 , сек. (3-2)
, сек. (3-2)
оно показывает, что здесь имеется лишь свободный ток. который затухает по экспоненте с постоянной времени
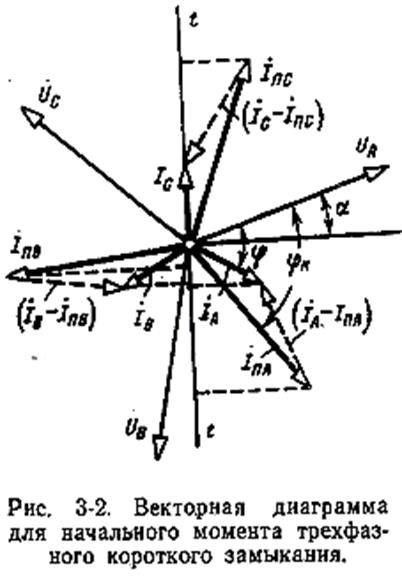
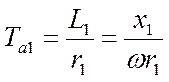 , сек. (3-3)
, сек. (3-3)
Начальное значение свободного тока в каждой фазе зашунтированного участка цепи, очевидно, равно предшествовавшему мгновенному значению тока, поскольку в цепи с индуктивностью не может произойти внезапного (скачком) изменения тока. В общем случае свободные токи в фазах различны, хотя их затухание, разумеется, происходит с одной и той же постоянной времени. В одной из фаз свободный ток может вообще отсутствовать, если в момент возникновения
короткого замыкания предшествовавший ток в этой фазе проходил через нуль; при этом свободные токи в двух других фазах будут одинаковы по величине, но противоположны по направлению.
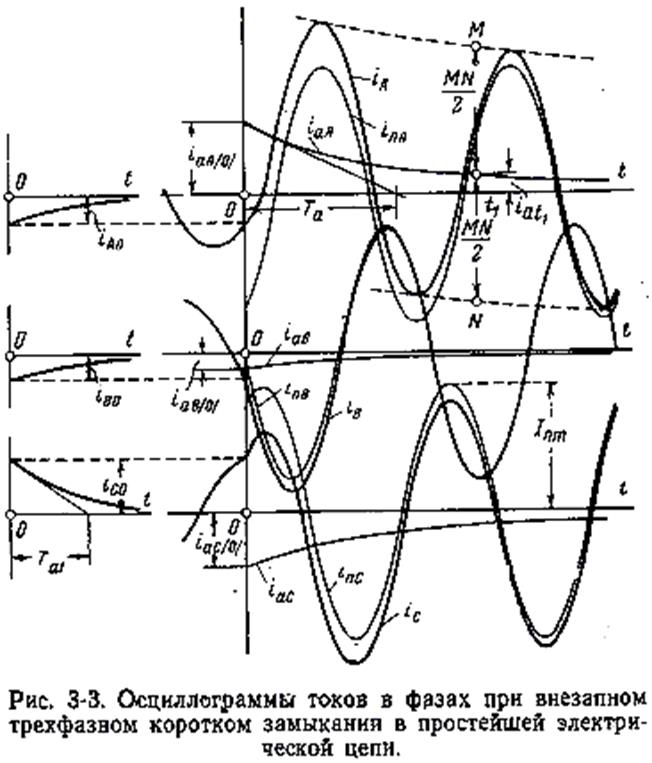 На рис. 3-3 слева приведены кривые изменения фазных токов в зашунтированном участке рассматриваемой цепи, с учетом, что короткое замыкание произошло в момент, отвечающий положению векторов на рис. 3-2.
На рис. 3-3 слева приведены кривые изменения фазных токов в зашунтированном участке рассматриваемой цепи, с учетом, что короткое замыкание произошло в момент, отвечающий положению векторов на рис. 3-2.
Напомним, что подкасательная в любой точке экспоненты в принятом для оси времени масштабе дает значение постоянной времени, с которой происходит изменение экспоненты (рис. 3-3). Имея в виду, что при 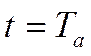 значение
значение 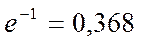 , постоянную
, постоянную 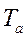 обычно трактуют как время, в течение которого переменная величина снижается до 0,368 своего начального значения; при этом за начальную может быть принята любая точка кривой.
обычно трактуют как время, в течение которого переменная величина снижается до 0,368 своего начального значения; при этом за начальную может быть принята любая точка кривой.
Перейдем теперь к участку цепи, который остался присоединенным к источнику. Здесь помимо свободного тока будет новый принужденный ток, величина которого, очевидно, больше предыдущего и сдвиг по фазе которого в общем случае иной. Допустим, что векторы 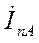 ,
, 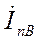 ,
, 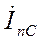 (рис. 3-2) отвечают новому установившемуся режиму данного участка цепи.
(рис. 3-2) отвечают новому установившемуся режиму данного участка цепи.
Дифференциальное уравнение равновесия для любой фазы, например фазы А, этого участка
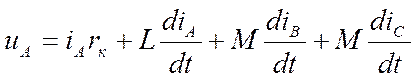 ,
,
имея в виду, что 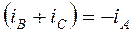 , можно представить (опуская индекс фазы) как
, можно представить (опуская индекс фазы) как
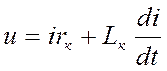 , (3-la)
, (3-la)
где 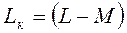 — результирующая индуктивность фазы, т. е. индуктивность с учетом влияния двух других фаз.
— результирующая индуктивность фазы, т. е. индуктивность с учетом влияния двух других фаз.
Решение (3-1а) имеет вид:
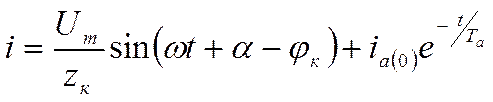 , (3-2a)
, (3-2a)
где 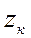 — полное сопротивление присоединенного к источнику участка цепи или, короче, цепи короткого замыкания;
— полное сопротивление присоединенного к источнику участка цепи или, короче, цепи короткого замыкания; 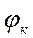 — угол сдвига тока в этой цепи;
— угол сдвига тока в этой цепи; 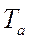 — постоянная времени цепи короткого замыкания, определяемая по (3-3), где вместо
— постоянная времени цепи короткого замыкания, определяемая по (3-3), где вместо 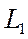 ,
, 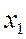 ,
, 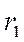 следует ввести
следует ввести 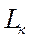 ,
, 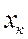 ,
, 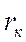 .
.
Первый член правой части (3-2а) представляет периодическую слагающую тока, которая при рассматриваемых условиях является принужденным током с постоянной амплитудой 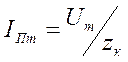 . Соответственно второй член представляет, как и раньше, затухающий по экспоненте свободный ток; его называют также апериодической слагающей тока. Начальное значение этой слагающей определяется из начальных условий, т. е.
. Соответственно второй член представляет, как и раньше, затухающий по экспоненте свободный ток; его называют также апериодической слагающей тока. Начальное значение этой слагающей определяется из начальных условий, т. е.
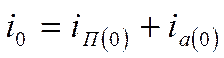 , (3-3)
, (3-3)
откуда после подстановки соответствующих выражений имеем:
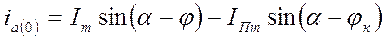 . (3-4)
. (3-4)
Поскольку токи 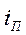 и
и 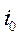 являются проекциями векторов
являются проекциями векторов 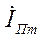 и
и 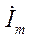 на линию времени, то ток
на линию времени, то ток 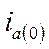 также можно рассматривать как проекцию вектора
также можно рассматривать как проекцию вектора 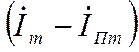 на ту же линию (рис. 3-2). В зависимости от фазы включения
на ту же линию (рис. 3-2). В зависимости от фазы включения 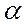 начальное значение тока
начальное значение тока 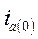 может изменяться от возможной наибольшей величины, когда вектор
может изменяться от возможной наибольшей величины, когда вектор 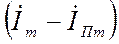 параллелен линии времени, до нуля, когда этот вектор нормален к ней. В трехфазной системе такие частные условия, разумеется, могут быть лишь в одной из фаз.
параллелен линии времени, до нуля, когда этот вектор нормален к ней. В трехфазной системе такие частные условия, разумеется, могут быть лишь в одной из фаз.
На рис. 3-3 справа представлены кривые изменения токов в фазах рассматриваемого участка при трехфазном коротком замыкании. Как видно, чем больше апериодическая слагающая тока, тем больше смещение кривой полного тока относительно оси времени. Эту слагающую можно рассматривать как криволинейную ось симметрии кривой полного тока, из которой ее легко выделить. Для этого нужно сначала провести огибающие по максимальным положительным и отрицательным значениям заданной кривой тока (см. пунктирные линии у кривой тока фазы А на рис. 3-3). Каждая точка кривой апериодической слагающей лежит посредине вертикального отрезка между этими огибающими.
 Из (3-4) и рис. 3-2 следует, что наибольшее значение апериодической слагающей тока определяется не только фазой включения, но также предшествующим режимом цепи. Так, например, при отсутствии предшествующего тока в данной цепи величина
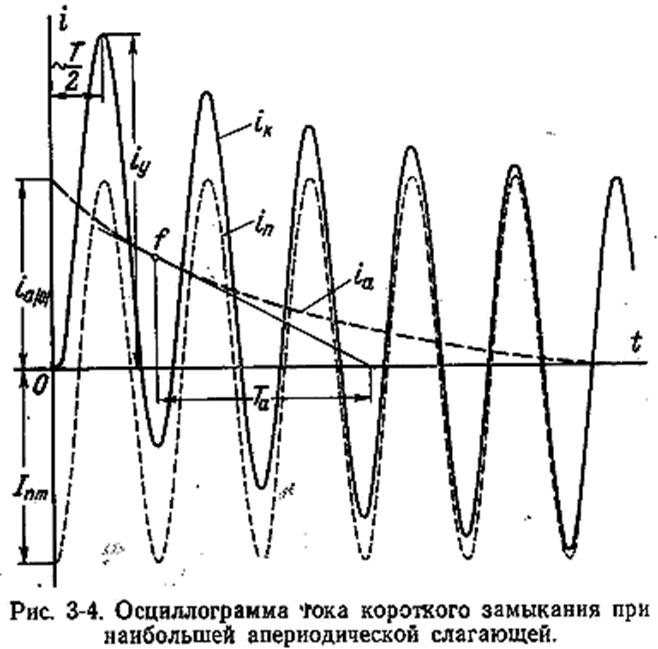
Из (3-4) и рис. 3-2 следует, что наибольшее значение апериодической слагающей тока определяется не только фазой включения, но также предшествующим режимом цепи. Так, например, при отсутствии предшествующего тока в данной цепи величина 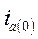 может достигать амплитуды периодической слагающей, если в момент короткого замыкания эта слагающая проходит через свой положительный или отрицательный максимум (рис. 3-4). Обычно этот случай рассматривается как расчетный.
может достигать амплитуды периодической слагающей, если в момент короткого замыкания эта слагающая проходит через свой положительный или отрицательный максимум (рис. 3-4). Обычно этот случай рассматривается как расчетный.
Важно отметить, что фаза включения, при которой возникает наибольшее значение апериодической слагающей, еще не предопределяет того, что именно три ней будет максимум мгновенного значения полного тока. В самом деле, из (3-2а) и (3-4) при отсутствии предшествующего тока 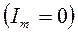 следует, что полный ток в цепи короткого замыкания является функцией двух независимых переменных: времени t и фазы включения
следует, что полный ток в цепи короткого замыкания является функцией двух независимых переменных: времени t и фазы включения 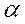 и выражается уравнением
и выражается уравнением
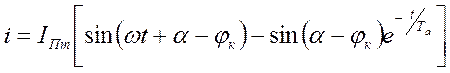 (3-5)
(3-5)
Приравняв нулю частные производные этого уравнения, т. е.
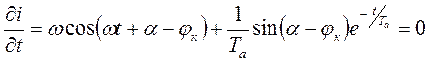 ;
;
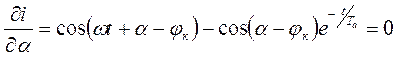 ,
,
и совместно решив эти уравнения, найдем, что максимум тока наступает при
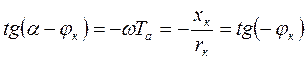 , т. е. при
, т. е. при 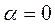 .
.
Следовательно, в предварительно разомкнутой цепи с r и L максимум мгновенного значения полного тока при коротком замыкании наступает, если в момент возникновения короткого напряжение источника проходит через нуль.
Для цепей с преобладающей индуктивностью 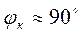 , поэтому условие возникновения наибольшей апериодической слагающей и условие, при котором достигается максимум мгновенного значения полного тока очень близки друг к другу. Поэтому в практических расчетах максимальное мгновенное значение полного тока короткого замыкания, которое называют ударным током короткого замыкания
, поэтому условие возникновения наибольшей апериодической слагающей и условие, при котором достигается максимум мгновенного значения полного тока очень близки друг к другу. Поэтому в практических расчетах максимальное мгновенное значение полного тока короткого замыкания, которое называют ударным током короткого замыкания 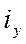 , обычно находят при наибольшем значении апериодической слагающей (рис. 3-4), считая, что он наступает приблизительно через полпериода, что при f=50 Гц составляет около 0,01 сек с возникновения короткого замыкания.
, обычно находят при наибольшем значении апериодической слагающей (рис. 3-4), считая, что он наступает приблизительно через полпериода, что при f=50 Гц составляет около 0,01 сек с возникновения короткого замыкания.
Таким образом, выражение для ударного тока короткого замыкания можно записать в следующем виде:
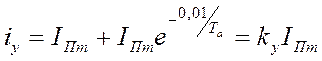 (3-6)
(3-6)
где 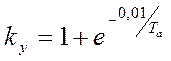 , (3-7)
, (3-7)
который называют ударным коэффициентом, показывает превышение ударного тока над амплитудой периодической слагающей; его величина находится в пределах 1< 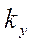 <2, что соответствует предельным значениям
<2, что соответствует предельным значениям 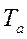 , т. е.
, т. е. 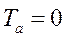 (при LK=0) и
(при LK=0) и 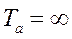 (при rк=0).
(при rк=0).
Естественно, чем меньше 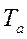 , тем быстрее затухает апериодическая слагающаяи тем соответственно меньше ударный коэффициент. Влияние этой слагающей сказывается лишь в начальной стадии переходного процесса; в сетях и установках высокого напряжения она практически исчезает спустя 0,1—0,3 сек, а в установках низкого напряжения она практически совсем незаметна.
, тем быстрее затухает апериодическая слагающаяи тем соответственно меньше ударный коэффициент. Влияние этой слагающей сказывается лишь в начальной стадии переходного процесса; в сетях и установках высокого напряжения она практически исчезает спустя 0,1—0,3 сек, а в установках низкого напряжения она практически совсем незаметна.
Еще раз подчеркнем, что апериодические слагающие токов в фазах различны. Поэтому определение трехфазного короткого замыкания как симметричного, строго говоря, справедливо применительно к периодическим слагающим фазных токов.
Дата добавления: 2015-02-10; просмотров: 2492;
