Короткое замыкание цепи
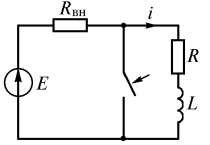 Для представленной на рис. 4.7 схемы требуется определить закон изменения тока в ветви с катушкой и напряжения на ней после коммутации. Выразим переходный ток через катушку в виде суммы установившейся и свободной составляющих
Для представленной на рис. 4.7 схемы требуется определить закон изменения тока в ветви с катушкой и напряжения на ней после коммутации. Выразим переходный ток через катушку в виде суммы установившейся и свободной составляющих
 (4.5)
(4.5)
Так как в контуре 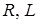 после коммутации нет источника
после коммутации нет источника
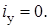 (4.6)
(4.6)
Для определения свободной составляющей запишем
Рис. 4.7 уравнение по второму закону Кирхгофа
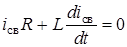 .
.
Характеристическое уравнение имеет вид 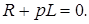
Общее решение для свободной составляющей
 , (4.7)
, (4.7)
где А – постоянная интегрирования; 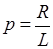 , с–1 – корень характеристического уравнения.
, с–1 – корень характеристического уравнения.
Для определения постоянной интегрирования воспользуемся начальным условием при  = 0
= 0
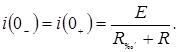
С учетом (4.5...4.7) получим
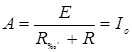 . (4.8)
. (4.8)
Подставив (4.8) в (4.7), а затем (4.7) и (4.6) в (4.5), получим переходный ток
 , (4.9)
, (4.9)
где τ – постоянная времени цепи, рассчитываемая по формуле
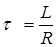 . (4.10)
. (4.10)
Подставим (4.10) в (4.7)
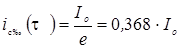 .
.
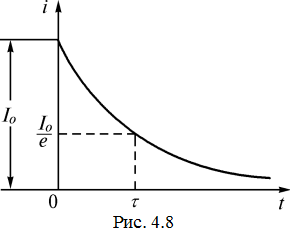
Таким образом, постоянная времени – время, в течение которого свободная составляющая процесса уменьшается в 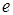 = 2,72 раза по сравнению с начальным значением.
= 2,72 раза по сравнению с начальным значением.
График изменения переходного тока показан на рис. 4.8.
ЭДС самоиндукции катушки
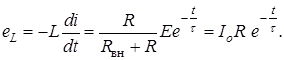
 (4.11)
(4.11)
В момент коммутации эта ЭДС равна напряжению на сопротивлении 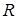 , а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.
, а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.
1. При коротком замыкании цепи 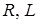 ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.
ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.
2. Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление контура.
3. Переходный процесс заканчивается при 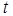 » 5
» 5 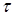 .
.
4. Напряжение на катушке в начальный момент времени равно напряжению на резисторе
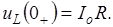
Дата добавления: 2015-03-19; просмотров: 2263;
