КИНЕТИКА ФЕРМЕНТАТИВНЫХ РЕАКЦИЙ

Ферментативная кинетика исследует влияние химической природы реагирующих веществ (ферментов, субстратов) и условий их взаимодействия (рН среды, температура, концентрация, присутствие активаторов или ингибиторов) на скорость ферментативной реакции. Скорость ферментативной реакции (u) измеряют по убыли количества субстрата или приросту продукта реакции за единицу времени.

При низкой концентрации субстрата скорость реакции

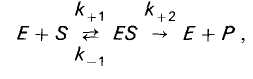
прямо пропорциональна его концентрации. При высокой концентрации субстрата, когда все активные центры фермента заняты субстратом (насыщение фермента субстратом), скорость реакции максимальна, становится постоянной и не зависящей от концентрации субстрата [S] и полностью зависит от концентрации фермента (рис. 19).

K_S – константа диссоциации фермент-субстратного комплексаES, обратна константе равновесия:

.

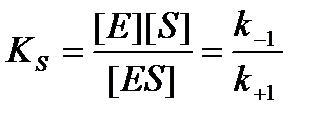Чем меньше значение K_S, тем выше сродство фермента к субстрату.

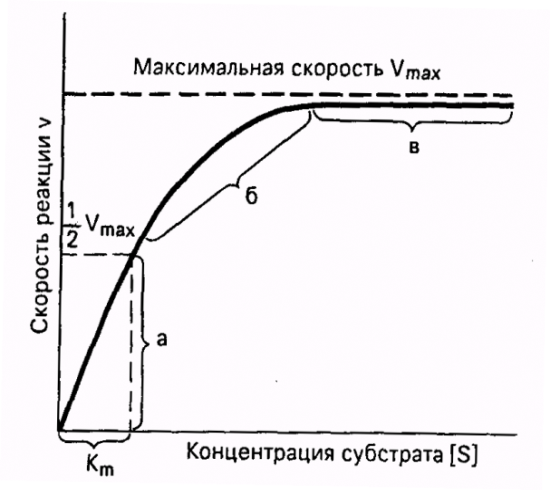
Рис. 19. Зависимость скорости ферментативной реакции от концентрации субстрата при постоянной концентрации фермента

Количественное соотношение между концентрацией субстрата и скоростью ферментативной реакции выражает уравнение Михаэлиса-Ментен:

,

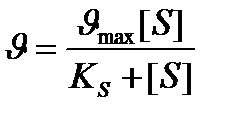u - скорость реакции, u_max - максимальная скорость ферментативной реакции.

Бриггс и Холдейн усовершенствовали уравнение, введя в него константу Михаэлиса K_m, определяемую экспериментально.

Уравнение Бриггса – Холдейна:

,

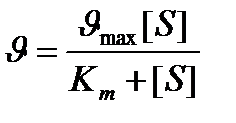где

.

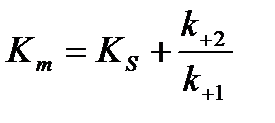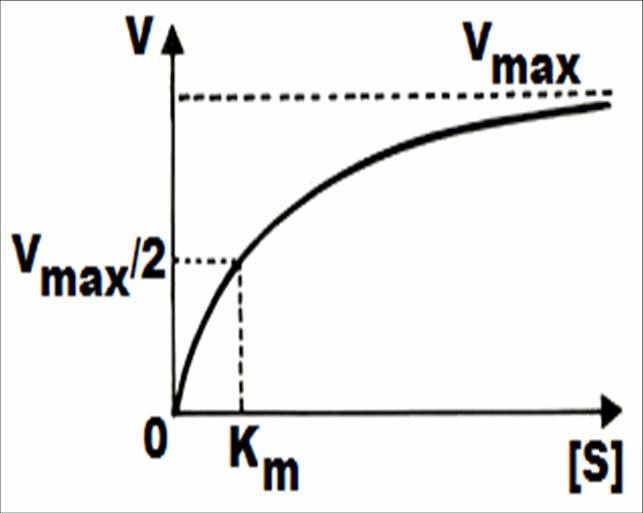
Константа Михаэлиса численно равна концентрации субстрата (моль/л), при которой скорость ферментативной реакции составляет половину от максимальной (рис. 20). К_m показывает сродство фермента к субстрату: чем меньше ее значение, тем больше сродство.

Рис. 20. Графическое определение константы Михаэлиса

Экспериментальные значения К_m для большинства ферментативных реакций с участием одного субстрата обычно 10^-2-10^{-5 М. Если реакция обратима, то взаимодействие фермента с субстратом прямой реакции характеризуется К}_m, отличающейся от таковой для субстрата обратной реакции.

Г. Лайнуивер и Д. Берк преобразовали уравнение Бриггса – Холдейна и получили уравнение прямой линии: у = ах + b (рис. 21):

.

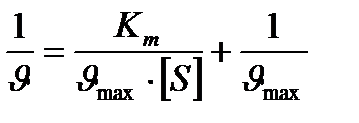Метод Лайнуивера – Берка дает более точный результат.

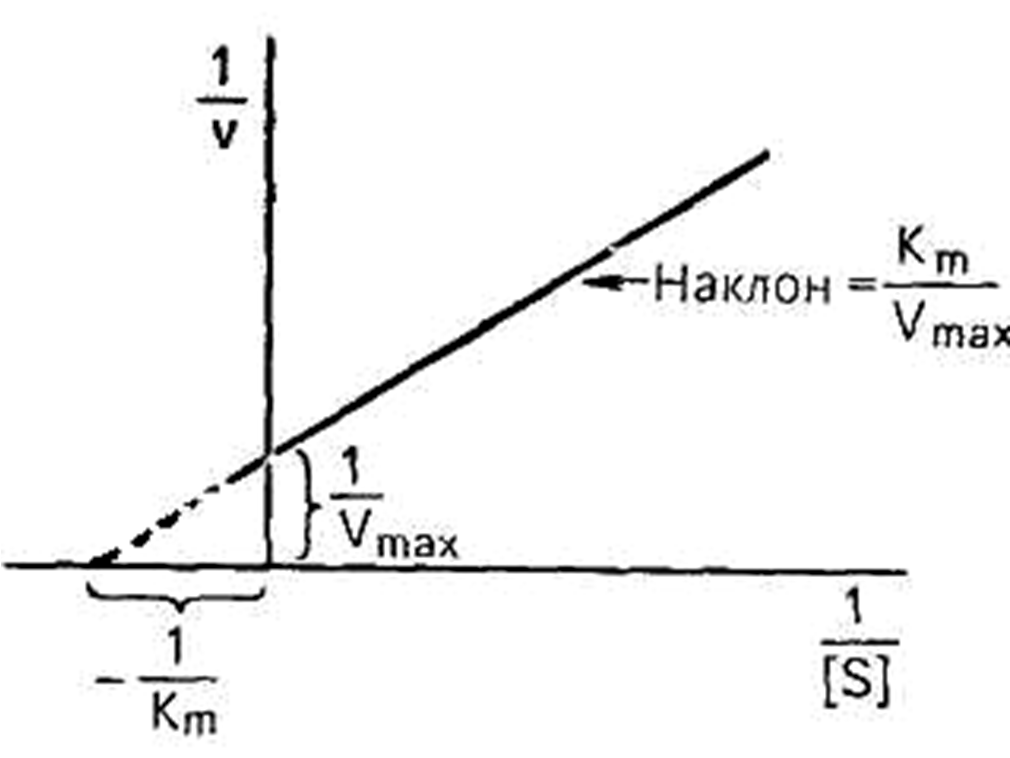
Рис. 21. Графическое определение константы Михаэлиса

по методу Лайнуивера-Берка