Наращение и дисконтирование потоков денежных сумм
 В реальной практике, как правило, приходится иметь дело не с единичными суммами, а с некоторыми потоками денежных сумм, которые регулярно предприятие реально выплачивает либо получает. Денежный поток принято изображать на временной линии
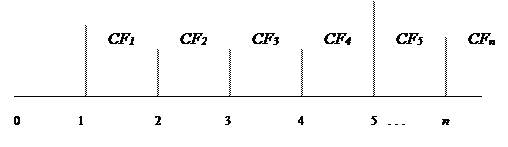
В реальной практике, как правило, приходится иметь дело не с единичными суммами, а с некоторыми потоками денежных сумм, которые регулярно предприятие реально выплачивает либо получает. Денежный поток принято изображать на временной линии  , как это показано на рисунке.
, как это показано на рисунке.
Элемент денежного потока принято обозначать CFk (от Cash Flow), где k - номер периода, в который рассматривается денежный поток. Настоящее значение денежного потока обозначено PV ( Present Value), а будущее значение - FV ( Future Value).
Наращение денежных потоков осуществляется с помощью многократного использования формулы (4.7):
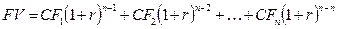 ,
,
или
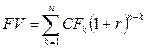 . (4.20)
. (4.20)
Пример. После внедрения мероприятия по снижению административных издержек предприятие планирует получить экономию $1,000 в год. Сэкономленные деньги предполагается размещать на депозитный счет (под 5 % годовых) с тем, чтобы через 5 лет накопленные деньги использовать для инвестирования. Какая сумма окажется на банковском счету предприятия?
Решим задачу с использованием временной линии.
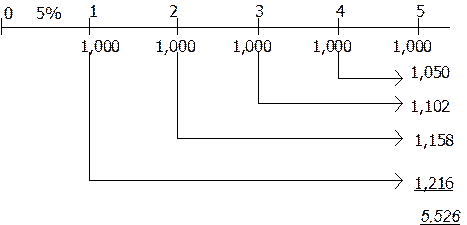
Таким образом, через 5 лет предприятие накопит $5,526, которые сможет инвестировать.
В данном случае денежный поток состоит из одинаковых денежных сумм ежегодно. Такой поток называется аннуитетом. Для вычисления будущего значения аннуитета используется формула
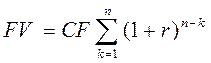 , (4.21)
, (4.21)
которая следует из (4.20) при CFk = const.
Расчет будущего значения аннуитета может производиться с помощью специальных финансовых таблиц. Фрагмент этих таблиц помещен в приложении (таблица 2). В частности, с помощью таблицы 2 при r = 5% и n = 5 получаем множитель 5,526, который соответствует результату расчета примера.
Для произвольного значения процентной ставки можно воспользоваться следующей конечной формулой для наращения аннуитета, которая легко получается путем использования суммирования убывающей геометрической прогрессии:
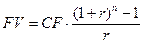 . (4.211)
. (4.211)
Дисконтирование денежных потоков осуществляется путем многократного использования формулы (4.8), что в конечном итоге приводит к следующему выражению:
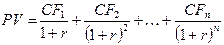 ,
,
или
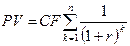 . (4.22)
. (4.22)
Пример. Рассмотрим денежный поток с неодинаковыми элементами CF1=100, CF2=200, CF3=200, CF4=200, CF5=200, CF6=0, CF7=1,000, для которого необходимо определить современное значение (при показателе дисконта 6%). Решение проводим с помощью временной линии:
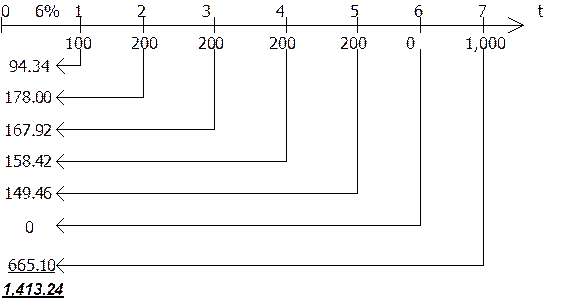
Вычисление дисконтированных значений отдельных сумм можно производить путем использования таблицы 3, помещенной в приложении.
Дисконтирование аннуитета (CFj = const) осуществляется по формуле
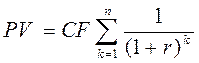 . (4.23)
. (4.23)
Для расчета настоящего (современного) значения аннуитета может быть использована таблица 4 приложения или следующее конечное соотношение:
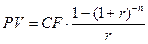 . (4.231)
. (4.231)
Пример. Предприятие приобрело облигации муниципального займа, которые приносят ему доход $15,000, и хочет использовать эти деньги для развития собственного производства. Предприятие оценивает прибыльность инвестирования получаемых каждый год $15,000 в 12 %. Необходимо определить настоящее значение этого денежного потока.
Решение проведем с помощью таблицы:
| Год | Множитель при 12% дисконтирования | Поток денег | Настоящее значение |
| 0.893 | $15,000 | $13,395 | |
| 0.797 | $15,000 | $11,955 | |
| 0.712 | $15,000 | $10,680 | |
| 0.636 | $15,000 | $9,540 | |
| 0.567 | $15,000 | $8,505 | |
| 3.605 | $75,000 | $54,075 |
По результатам расчетов мы видим, что
дисконтированное значение денежного потока существенно меньше арифметической суммы элементов денежного потока,
чем дальше мы заходим во времени, тем меньше настоящее значение денег: $15,000 через год стоят сейчас $13,395; $15,000 через 5 лет стоят сейчас $8,505.
Задача может быть решена также с помощью таблицы 4 приложения. При r = 12% и n = 5 по таблице находим множитель дисконтирования 3.605.
Современное значение бесконечного (по времени) потока денежных средств определяется по формуле:
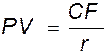 , (4.24)
, (4.24)
которая получается путем суммирования бесконечного ряда, определяемого формулой (4.23) при 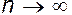 .
.
Дата добавления: 2015-02-05; просмотров: 1343;
