Логическая модель

В основе логической модели лежит формальная система, задаваемая четверкой вида: M = <T, P, A, B>, где T - множество базовых элементов различной природы; P - множество синтаксических правил; A Ì Р - аксиомы; B - множество правил вывода.

Множество Т может включать, например, слова из некоторого ограниченного словаря, детали детского конструктора, входящие в состав некоторого набора и т.п. Важно, что для множества T существует некоторый способ определения принадлежности или не принадлежности произвольного элемента к этому множеству. Процедура такой проверки может быть любой, но за конечное число шагов она должна давать положительный или отрицательный ответ на вопрос, является ли x элементом множества T. Обозначим эту процедуру П(T).

С помощью правил Р из элементов T образуют синтаксически правильные совокупности, так называемые правильно построенные формулы (ППФ). Например, из слов ограниченного словаря строятся синтаксически правильные фразы, из деталей детского конструктора с помощью гаек и болтов собираются новые конструкции. Декларируется существование процедуры П(P), с помощью которой за конечное число шагов можно получить ответ на вопрос, является ли совокупность X синтаксически правильной. Аналогичная процедура П(A) должна существовать для ответа на вопрос о принадлежности ППФ к множеству A.

Применяя правила вывода к элементам A, можно получать новые ППФ, к которым снова можно применять правила из B. Так формируется множество выводимых в данной формальной системе совокупностей. Если имеется процедура П(B), с помощью которой можно определить для любой синтаксически правильной совокупности, является ли она выводимой, то соответствующая формальная система называется разрешимой. Это показывает, что именно правило вывода является наиболее сложной составляющей формальной системы.

Если в качестве элементов множества Р выступают высказывания, то формальная система М моделирует исчисление высказываний; если роль элементов множества Р играют предикатные символы, то формальная система М является представлением исчисления предикатов.

Для знаний, хранящихся в памяти компьютера, можно считать, что множество A образуют все информационные единицы, которые введены в компьютер извне, а с помощью правил вывода из них выводятся новые производные знания. Свойство логических моделей получать новое знание делает их притягательными для использования: оно позволяет хранить в базе лишь те знания, которые образуют множество A, а все остальные знания получать из них по правилам вывода.

В таких моделях представляются и декларативные знания – через формулы и процедурные- через правила вывода. Преимущества – лаконичность представления, наличие логического вывода, позволяющего получить новое знание. Недостаток – отсутствие наглядности и излишняя формализованность, сложность понимания логических формул, громоздкость. Такие модели применяются в сочетании с другими.

Построим логическую модель, соответствующую задаче «Регулирование успеваемости по результатам сессии» (см. разделы 4.3.1, 4.3.2). Поскольку введенные выше правила перевода или отчисления студентов носят обобщенный характер (т.е. касаются студентов в целом), используем в качестве формального аппарата для модели исчисление предикатов.

В качестве элементов множества Т используем понятиястудент, размер стипендии, функциональные символы, соответствующие требуемым в модели действиям - отчислить (студент), перевести в следующий семестр (студент), назначить стипендию (студент, размер стипендии), предикатные символы, соотнесенные с условиями, существенными для принимаемых по студентам решений, - иметь оценку=2(студент), иметь оценку=3(студент), иметь оценку=4(студент). Используем также квантор ":= «для каждого», логические связки «отрицание» - ù , «конъюнкция» - Ù.

В соответствии с правилами принятия решений по студентам определим аксиоматику А моделируемой предметной области:

"студент. (иметь оценку=2(студент))Þ отчислить (студент);

"студент. (ù(иметь оценку=2(студент)))Þ перевести в следующий семестр (студент);

"студент. (ù(иметь оценку=2(студент))Ù ù (иметь оценку=3(студент))Ù (иметь оценку=4(студент)))Þ назначить стипендию (студент, 600);

"студент. (ù(иметь оценку=2(студент))Ùù (иметь оценку=3(студент))Ùù (иметь оценку=4(студент)))Þ назначить стипендию (студент, 600).

В качестве правила вывода из В используем правило modus ponens вида 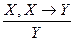, где над чертой – множество посылок и аксиом, под чертой – заключение.

Пусть студент Попов имеет в сессию двойку. Тогда посылка Х запишется как (иметь оценку=2(Попов)). Принятие решения по этому студенту выглядит как логический вывод:

(иметь оценку=2(Попов)), "студент. (иметь оценку=2(студент))Þ отчислить (студент)

отчислить (Попов)

Совокупность представлений знаний в компьютере формирует базу знаний (БЗ) предметной области. Возможность представления знаний в компьютере позволяет использовать новый методологический подход к созданию и эксплуатации сложных систем, который основан на применении «искусственного интеллекта». В настоящий момент можно выделить следующие направления в реализации информационных технологий, применяющих данные принципы:

1) интеллектуальные информационно-поисковые системы, обеспечивающие в процессе диалога взаимодействие конечных пользователей с БД и БЗ на профессиональных языках, близких к естественному. Пользователь формирует запросы к системе, а она их обрабатывает и генерирует ответы;

2) расчетно-логические системы, позволяющие конечным пользователям решать в диалоговом режиме свои задачи на компьютере с использованием сложных математических методов и соответствующих прикладных программ;

3) экспертные системы, дающие возможность осуществить эффективную компьютеризацию слабо структурированных областей, в которых знания могут быть представлены в экспертной описательной форме, но использование математических моделей, характерных для точных наук, затруднительно, а иногда и невозможно.