Сетевая модель
Сетевые модели формально можно задать в виде H = <I, C1, C2, ..., Cn, Г>. Здесь I есть множество информационных единиц – вершин сети; C1, C2, ..., Cn - множество типов связей между информационными единицами – дуг сети. Отображение Г задает между информационными единицами, входящими в I, связи из заданного набора типов связей.
Информационные единицы (вершины) сети классифицируются следующим образом:
1) обобщенные – некоторое известное и широко используемое в моделируемой среде понятие, например, кафедра, принтер. Представляет класс объектов моделируемой среды;
2) конкретные (индивидные) – каким-либо образом выделенная единичная (индивидная) сущность, например, кафедра СУиВТ, компьютер с регистрационным номером 123456789. Отнесение понятия к обобщенному или конкретному классу относительно и зависит от предметной области и решаемых задач;
3) агрегатные – объекты предметной области, составленные тем или иным образом из других объектов, являющихся его частями. Для выделения агрегатного объекта важно, чтобы его части были существенны для решаемой задачи. Например, кафедра СУиВТ может рассматриваться как агрегатный объект, включающий ряд лабораторий, если речь идет о составлении расписания занятий; в состав принтера входит картридж – это существенно, когда речь идет о пополнении тонера.
Различают следующие типы связей:
1) парадигматические – задают устойчивые отношения между понятиями предметной области, представляемыми информационными единицами. Включают виды связей:
§ связь структуризации - задает иерархию информационных единиц. Состоит из связей:
Ø род-вид. Существует между обобщенными и конкретными информационными единицами, например, это связь между понятиями принтер и периферия компьютера;
Ø часть-целое. Может устанавливаться между агрегатной информационной единицей и той, которая входит в ее состав;
Ø класс-подкласс;
§ каузальная связь (причина-следствие);
2) функциональные – задают аналитические отношения между информационными единицами, т.е. несут процедурную информацию, позволяющую находить (вычислять) одни информационные единицы через другие;
3) лингвистические – связи, определяющие отношения между языковыми знаками, обозначающими понятия предметной области, например, синонимию, омонимию, антонимию;
4) семантические – все остальные типы связей.
В зависимости от типов связей, используемых в модели, различают: классифицирующие сети, функциональные сети и сценарии. В классифицирующих сетях используются отношения структуризации. Такие сети позволяют при представлении знаний вводить различные иерархические отношения между информационными единицами. Функциональные сети характеризуются наличием функциональных отношений. Их часто называют вычислительными моделями, т.к. они позволяют описывать процедуры "вычислений" одних информационных единиц через другие. В сценариях используются каузальные отношения, а также отношения типов "средство - результат", "орудие - действие" и т.п. Если в сетевой модели допускаются все типы связей, она называется семантической сетью.
В зависимости от арности связей различают однородные сети, когда все связи одинаковой арности (бинарные, тернарные, квадринарные и т.д.), и неоднородные.
Для арности больше двух вводят специальные вершины, которые обозначают не информационные единицы, а связи между ними. Так, связь, соответствующая понятию полная семья и имеющая арность 3, а также связанные с ней вершины представляются сетью, показанной на рисунке 5.2:
полная семья
дети отец мать
Рисунок 5.2 – Пример тернарной связи
В зависимости от возможностей отражения состояния связи различают сети:
1) дискретные. Связь имеет только два состояния: она либо есть, либо ее нет;
2) аналоговые. Связь нагружается величиной проходимости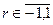 
, которая выражает силу связи. Это позволяет отражать кванторы, например, r = -1 – никогда (ù$), r = 0 - существует ($), r = 1 – для каждого (").
С помощью аналоговой сети можно представить знания о модальности получения среднего и высшего образования. Пусть вершинами сети будут понятия человек, ВУЗ, школа (по введенной ранее классификации они относятся к обобщенным понятиям), связь соответствует отношению обучаться.
|
ВУЗ школа
человек
Рисунок 5.3 – Пример аналоговой сети
Достоинство сетевых моделей – простота, наглядность, высокая степень структуризации знаний, относительная свобода представления знаний. Недостаток – нерегулярность структуры.
Построим сетевую модель, соответствующую задаче «Регулирование успеваемости по результатам сессии» (см. разделы 4.3.1, 4.3.2). В качестве вершин сети используем понятия: студент, ФИО, оценки, значения оценок, стипендия, значение стипендии, следующий семестр. Выделение именно таких понятий отчасти субъективно, например, можно было бы не вводить вершины-значения. Введем связи и их обозначения: иметь характеристикой - 1, иметь результатом - 2, иметь значением – 3, получать – 4, быть переведенным – 5. Поскольку не каждый студент получает стипендию и не всякий студент переводится в следующий семестр, введем для связей 4 и 5 величины проходимости r4 и r5 , соответственно. Чтобы показать возможность существования той или иной оценки у студента, введем величину проходимости и на связи 3 для оценок – r3. Полученная сеть показана на рисунке 5.4.
Чтобы придать сети свойство вырабатывать решения, конкретизируем обобщенную сеть рисунка 5.4 значениями данных, которые эти решения определяют. Получим сети рисунков 5.5 – 5.8.
Рисунок 5.4 – Сеть, соответствующая задаче «Регулирование успеваемости по результатам сессии»
Рисунок 5.5 – Сеть, соответствующая решению об отчислении студента: r3 =0, следовательно, r4 =-1, r5 = -1
Рисунок 5.6 – Сеть, соответствующая решению о переводе студента в следующий семестр: r3 =-1 для оценки=2, следовательно, r5 =1
Рисунок 5.7 – Сеть, соответствующая решению о назначении студенту базовой стипендии: r3 =-1 для оценки=3, следовательно, r4 =1 и стипендия=600
Рисунок 5.8 – Сеть, соответствующая решению о назначении студенту повышенной стипендии: r3 =-1 для оценки=4, следовательно, стипендия=900
Если теперь построить некоторый алгоритм, который будет по каждому студенту последовательно сопоставлять его оценки с представлениями сетей рисунков от 5.5. до 5.8, то при совпадении конкретных данных и структуры той или иной сети можно говорить о принятии соответствующего решения.
Иногда используют комбинации сетевых и продукционных моделей представления знаний. В таких моделях декларативные знания описываются в сетевом компоненте модели, а процедурные знания - в продукционном. В этом случае говорят о работе продукционной системы над семантической сетью.
Дата добавления: 2015-02-05; просмотров: 850;