Образцовые меры концентрации и градуировка
Прежде чем перейти к метрологическим вопросам, связанным с передачей размера единиц концентрации от исходных образцовых mcj) к рабочим средствам измерений, необходимо обратить внимание на современные тенденции развития методов химического анализа. В наиболее общем виде они проявляются при наукометрических исследованиях, один из результатов которых представлен в табл. 39.
Таблица 39
| Наименование метода | Доля публикаций По годам , % | |||
| Хрома то графия | ||||
| Газовая хроматография | ||||
| Спектроскопия (ЭПР,ЯМР, фотометрия) | ||||
| Электрохимические методы | ||||
| Химические методы (гравиметрия, титрометрия и т. п.) |
• Основной вывод, вытекающий из табл. 39, — ускоренное развитие инструментальных методов и, соответственно, резкое возрастание числа аналитических приборов. В настоящее время доля химических методов стабилизировалась на уровне 3 %. Такое перемещение центра тяжести с химических методов анализа на инструментальные физические привело к обострению проблемы обеспечения единства измерений концентрации. Почему это произошло? Причина в том, что химические методы в своем большинстве относятся к абсолютным методам, а следовательно, проблемы образцовых мер концентрации для них практически не существует. В то же время практически для каждого физического метода, для каждого анализируемого этим методом компонента уравнение связи устанавливается в результате градуировки по образцовым мерам концентрации данного компонента. Особенностью физических методов является то, что точность результатов измерений не может быть выше точности градуировки.
Аналитические приборы в зависимости от подходов к их градуировке делятся на две группы: универсальные и анализаторы состава. Уравнения связи для приборов обеих этих групп не известны.
Градуировка универсальных приборов, предназначенных для проведения количественного анализа, осуществляется в два этапа. На первом этапе производится передача размеров единиц тех физических величин, которые используются в дальнейшем для определения концентрации (обычная градуировка) . Для ее проведения используются эталоны и исходные образцовые меры единиц физических величин (см. разд. 6.1). На втором этапе определяется уравнение связи в виде градуировочной характеристики. Для этой цели используются образцовые меры концентрации, являющиеся аналогами наборов образцовых мер. Эти образцовые меры концентрации представляют собой смеси с известными по методу приготовления значениями концентрации компонентов в установленном диапазоне, получаемые из исходных образцовых веществ.
Таким образом, градуировка универсальных приборов производится с использованием двух видов мер: мер физических свойств, измерение которых положено в основу аналитического метода, и мер концентрации. Градуировка по мерам данной физической величины позволяет использовать универсальный прибор для количественного анализа не одного вещества, а целого их ряда, в связи с чем необходима дополнительная градуировка по образцовым мерам концентрации остальных компонентов.
Отличие анализаторов состава заключается в том,что для них уравнение связи в явном виде не устанавливается. Поэтому для этой группы приборов отпадает необходимость проводить измерения действительных значений физических свойств, т. е. отпадает необходимость в градуировке по первой группе мер. Основное требование, предъявляемое к анализаторам состава, заключается в стабильности их показаний. Поэтомуградуировка анализаторов состава производится только по образцовым мерам концентрации для нанесения шкалы концентрации. Типичным представителем данной группы шкальных приборов являются газоанализаторы.Измерения концентрации на приборах данной группы осуществляются в видепрямых отсчетов показаний шкалы. Недостатком данной группы приборов является жестко ограниченная узкая область применения.
Рассмотрим более подробно установление уравнений связи, представленных в общем виде уравнениями (39) и (40) . Для практического их использования они могут быть преобразованы в таблицы, графики и в функциональные уравнения.
Примерами таблиц являются таблицы спектральных линий в широком диапазоне длин волн, таблицы молекулярных спектров. Наиболее широкое употребление данная форма имеет при проведении качественного анализа.
В то же время графическое представление градуировочных функций преимущественно используется в количественном анализе. При этом, как правило, стремятся привести эту функцию к линейной. Для этого применяют различные математические преобразования, в частности, логарифмирование. В последнем случае при графическом изображении используют диаграммы с логарифмическими или полулогарифмическими координатами.
Наиболее точную градуировочную характеристику получают в третьем случае, когда эта характеристика выражается в аналитическом виде как полином третьей, реже четвертой степени.
Независимо от формы представления градуировочной характеристики (аналитической или графической) значения концентрации (сi), используемые при этом, рассматриваются как детерминированные величины. Это требует, в свою очередь, чтобы эти значения концентрации были известны с точностью, по крайней мере, в три раза превышающей точность измерения физического свойства, используемого в дальнейшем для нахождения аналитической функции данного метода.
Рассмотрим наиболее типичный случай, когда градуировочная функция может быть представлена в виде линейной:
wc=а + Ьс , (45)
где с — концентрация, которая может быть выражена в любых ее единицах.
Используя набор образцовых мер, представляющий ряд (т) значений концентрации (сi) во всем диапазоне измерений данным методом (cH – сK) и проведя для каждой меры ri параллельных измерений wi,c , получим
m
п = åri пар (сi ; wi,c),
i=1
которые позволяют установить конкретное линейное уравнение. Обычно конкретные значения коэффициентов 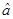 и
и 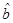 в уравнении (45) определяют методом наименьших квадратов.
в уравнении (45) определяют методом наименьших квадратов.
Эмпирическая градуировочная прямая будет
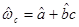 (46)
(46)
Проведение изложенной выше градуировки представляет собой только предварительный этап. При измерении концентрации приходится решать обратную задачу: для измеренного конкретного физического свойства (wc0) аналитической пробы следует установить соответствующее ему значение концентрации (с0) и оценить погрешность этого значения*.
Искомое значение концентрации ( 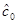 ) определяется из уравнения градуировочной прямой _
) определяется из уравнения градуировочной прямой _
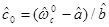 (47)
(47)
Для оценки случайной погрешности определения искомой
концентрации ( 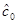 ) необходимо учесть:
) необходимо учесть:
1) погрешность градуировочной прямой;
2) погрешность измеряемого сигнала (wc0 ).
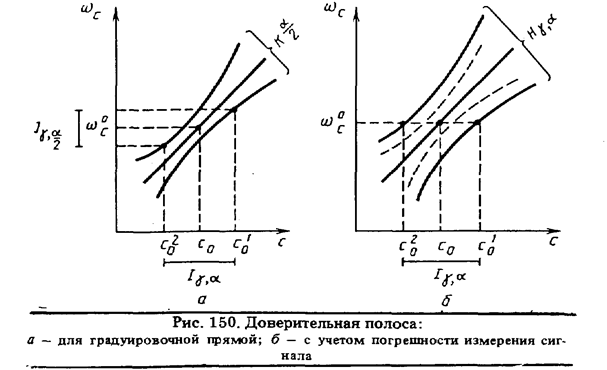
Погрешиость градуировочной прямой целесообразно оценивать не в виде доверительных границ для каждой экспериментальной точки, используемой для установления градуировочной функции, а в виде доверительной полосы при заданном уровне значимости (1 — а/2) для всего рабочего интервала концентраций (cH . . . сK), как это показано на рис. 150. Оценка ширины доверительной полосы А (с) 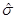 производится по уравнению
производится по уравнению
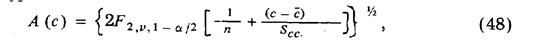
где F 2, v , 1 – а/2 — квантиль F-распределения с (2, v) степенями свободы; 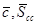 , -- среднее значение и границы разброса измеренных значений сi в эксперименте по градуировке,
, -- среднее значение и границы разброса измеренных значений сi в эксперименте по градуировке,
определяемые согласно 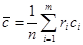 ;
; 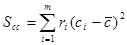
* Погрешность измерения — отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Необходимость в объяснении термина "погрешность измерения" вызвана тем, что в предыдущих главах учебника он не встречался. Появление его в гл. 6 объясняется различием в концептуальных подходах к теории точности измерении автора учебника И.Ф. Шишкина и Ю.И. Александрова, написавшего данную главу. Это отражает те тенденции в развитии метрологии, которые существуют на сегодняшний день;
одна из них сложилась давно и закреплена в многочисленных нормативных документах ГСИ (именно ее и придерживался Ю.И. Александров), другая, из которой исходил И.Ф. Шишкин, избавляет науку об измерениях от излишней зарегламентированности и открывает широкую возможность проникновения ее методов в другие науки и сферы деятельности человека. — Примеч. ред.)
Когда оценка s2 производится из результатов градуировочных экспериментов, используют уравнение
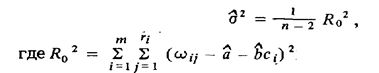
Погрешность измеряемого сигнала (wc0) в предположении о нормальном распределении экспериментальных данных оценивается в виде:
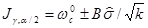 (49)
(49)
где В = Z1-g/2 [v/c2v, a ] ; cv, a/2 — нижний квантиль c2 — распределения с v степенями свободы; 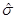 2 — оценка дисперсии s2 при v степенях свободы.
2 — оценка дисперсии s2 при v степенях свободы.
Таким образом, оценка случайной погрешности искомой концентрации ( 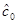 ) может быть произведена одним из следующих способов.
) может быть произведена одним из следующих способов.
1 способ. В этом случае используют результаты оценки доверительной полосы градуировочной прямой (рис. 150, а). На оси ординат откладывается среднее значение измеренного сигнала ( 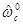 ) и его оценка в виде Ig,a . Проекции соответствующих им точек пересечения с нижней и верхней границей доверительной полосы градуировочной прямой на ось абсцисс позволяют найти максимальное (c02) и минимальное (с01) значения концентрации, определяющие интервальную оценку концентрации
) и его оценка в виде Ig,a . Проекции соответствующих им точек пересечения с нижней и верхней границей доверительной полосы градуировочной прямой на ось абсцисс позволяют найти максимальное (c02) и минимальное (с01) значения концентрации, определяющие интервальную оценку концентрации 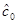 , соответствующей среднему значению
, соответствующей среднему значению 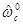 . Если бы градуировочная прямая была известна точно, то погрешность определения
. Если бы градуировочная прямая была известна точно, то погрешность определения 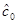 была бы обусловлена только погрешностью измерения
была бы обусловлена только погрешностью измерения 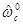 и соответствовала бы интервалу, заключенному между пунктирными прямыми.
и соответствовала бы интервалу, заключенному между пунктирными прямыми.
2 способ. В этом случае погрешность измерения 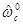 учитывают непосредственно в виде оценки Нg,a определяемой как
учитывают непосредственно в виде оценки Нg,a определяемой как
Нg,a = [A(c) + B/ 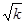 ]
] 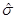 (50)
(50)
H откладывают в виде доверительной полосы на градуировочном графике (см. рис. 150, б). Оценка погрешности определения концентрации производится в результате проекции на ось абсцисс точек пересечения горизонтальной прямой, отвечающей среднему значению измеряемого сигнала ( 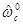 ) с верхней и нижней границами Нg,a Данный способ наиболее пригоден, когда число параллельных определений (k) при анализе неизвестной пробы всегда одинаково.
) с верхней и нижней границами Нg,a Данный способ наиболее пригоден, когда число параллельных определений (k) при анализе неизвестной пробы всегда одинаково.
Интервал Ig,a следует рассматривать как интервал значений концентраций 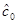 , при которых пробам с этими концентрациями соответствует с вероятностью (1 — g) диапазон измеряемых значений
, при которых пробам с этими концентрациями соответствует с вероятностью (1 — g) диапазон измеряемых значений 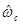 со средним значением
со средним значением 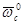
 .
.
Данный подход к оценке погрешности измерения концентрации позволяет дать определения таким понятиям как:
1. Предел обнаружения, относящийся к измеряемому аналитическому сигналу, wmin (Limit of Decision);
2. Предел обнаружения, относящийся к концентрации, cmin (Limit of Detection);
3. Нижняя граница определяемых концентраций (cопр. ) (Limit of Determination).
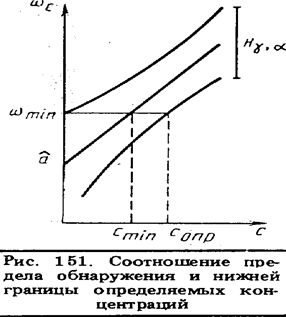
Пределом обнаружения как измеряемого аналитического сигнала, так и концентрации называют минимальное значение сигнала концентрации, которое может быть установлено с заданной доверительной вероятностью.
Предел обнаружения wmin представляет верхнее значение Нg,a, установленное для холостого опыта (с = 0) и на рис. 151 изображен в виде отрезка на оси ординат. Значение wmin определяют, используя градуировочное уравнение (46), также уравнения (48) и (50):
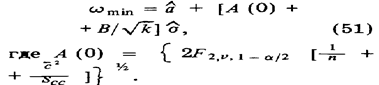
Предел обнаружения с mm определяют с учетом уравнений (51) и (47):
cmin = (wmin – 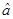 )/
)/ 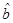 . (52)
. (52)
На рис. 151 показано, что графически с nun соответствует отрезок на оси абсцисс, получаемый как проекция на эту ось точки пересечения горизонтальной прямой, отвечающей wmin с градуировочной прямой.
Нижняя граница определяемых концентраций (сопр) представляет минимальное значение концентрации, для которого с уровнем значимости (1 — a) и с вероятностью не менее (1 — g/2)результат измерения сигнала 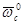 будет больше, чем предел его обнаружения (wmin )На рис. 151 cопр соответствует отрезок на оси абсцисс, получаемый как проекция на эту ось точки пересечения горизонтальной прямой, отвечающей wmin нижней границей Нg,a.
будет больше, чем предел его обнаружения (wmin )На рис. 151 cопр соответствует отрезок на оси абсцисс, получаемый как проекция на эту ось точки пересечения горизонтальной прямой, отвечающей wmin нижней границей Нg,a.
Важно отметить, что приведенные выше способы нахождения wmin ,cmin , cопр связаны с введением каких-либо конкретных коэффициентов типа Зs или 6s.
Широко распространена точка зрения, что проведение на этапе пробоподготовки концентрирования позволяет уменьшить нижнюю границу определяемых концентраций. Представленное на рис. 151 соотношение показывает ошибочность такого заключения (сопр зависит только от чувствительности метода измерения и метрологических характеристик используемых при этом средств измерений).
Прежде чем перейти к следующему разделу, где будут рассмотрены способы контроля правильности результатов химического анализа, необходимо сделать краткие выводы.
Выше бьет изложен подход к обеспечению единства измерений концентрации от проблем воспроизведения единиц концентрации, с учетом особенностей концентрации как физической величины, до вопросов передачи размера единиц концентрации в результате проведения градуировки.
Необходимо еще раз подчеркнуть, что независимо от того, какая система передачи размера единиц применяется для обеспечения единства измерений — децентрализованная или централизованная, используемые для передачи размера единиц средства измерений всегда выполняют функцию образцовых средств измерений, к которым и относят образцовые меры.
Наряду с образцовыми мерами, известен особый вид метрологических средств, обозначаемый как стандартные образцы. Появление стандартных образцов продиктовано объективным развитием метрологии. Однако следует провести четкую грань между образцовыми мерами и стандартными образцами, чему в значительной мере и будет посвящен следующий раздел.
Для предотвращения терминологической путаницы не следует применять термин "стандартный образец" к веществам с аттестованными метрологическими характеристиками, используемым для проведения градуировки.
Дата добавления: 2015-02-05; просмотров: 1918;
