Переходный режим
При t < tу (см. рис. 63, 64) режим работы средства измерений называется переходным. В этом режиме сказываются инерционные свойства средства измерений. Оно не успевает должным образом отреагировать на изменение входного воздействия Q (t), в результате чего выходной сигнал оказывается искаженным по сравнению с входным. В переходном режиме отклик средства измерений Х(t) не соответствует значению измеряемой величины, установленному при градуировке шкалы.
Переходный режим работы средства измерений описывается линейным или нелинейным дифференциальным уравнением динамики.
Пример 33.Чувствительный элемент термометра, показанного на рис. 63 резко опускается в среду с постоянной температурой Тср Полагая, что передача тепла к чувствительному элементу осуществляется с задержкой во времени, а длина столба термометрической жидкости пропорциональна ее температуре, составить уравнение, описывающее переходный режим работы термометра.
Решение. Уравнение теплового баланса в рассматриваемом случае записывается следующим образом,
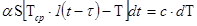
Левая часть этого уравнения представляет собой количество тепла, переданного средой чувствительному элементу за время dt Здесь а — коэффициент теплопередачи; S - площадь наружной поверхности чувствительного элемента, находящейся в контакте со средой 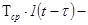 скачок температуры, подводимой к термометрической жидкости чувствительного элемента через время т после его погружения в среду с температурой Тcp; Т - температура термометрической жидкости. В правой части уравнения - количество тепла, полученного за то же время термометрической жидкостью с теплоемкостью с.
скачок температуры, подводимой к термометрической жидкости чувствительного элемента через время т после его погружения в среду с температурой Тcp; Т - температура термометрической жидкости. В правой части уравнения - количество тепла, полученного за то же время термометрической жидкостью с теплоемкостью с.
Обозначая через  постоянную времени термометра, называемую также постоянной термической инерции, получим
постоянную времени термометра, называемую также постоянной термической инерции, получим
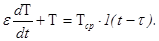
Пример 34.Груз, подвешенный к сжатой пружине динамометра резко отпускается (см. рис. 64). Составить уравнение динамики описывающее переходный режим работы динамометра.
Решение. Согласно второму закону Ньютона
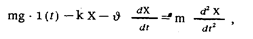
где равнодействующая сил, приложенных к грузу, слагается из силы тяжести, силы сжатия пружины (k - коэффициент жесткости пружины) и силы сопротивления среды (u- коэффициент сопротивления среды).
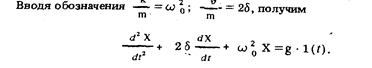
Пример 35.Составить уравнение динамики, описывающее переходный режим работы интегрирующего звена (см. рис 69) входящего в состав измерительной цепи, при подаче на его вход постоянного напряжения Uo.
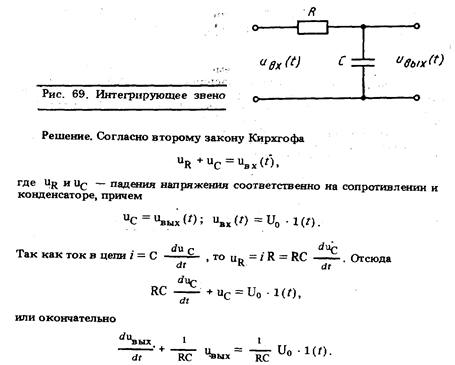
В общем случае у линейных средств измерений уравнение динамики является неоднородным линейным дифференциальным уравнением n-го порядка с постоянными коэффициентами:
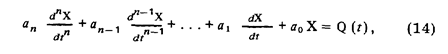
где Q (t) —известное входное воздействие, называемое также входным сигналом, вызывающим отклик на него средства измерения Х(t) — выходкой сигнал.
Классический метод решения уравнения д и н а м и к и. Решением неоднородного уравнения (14) является сумма общего решения Хо однородного уравнения
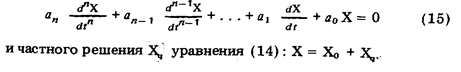
Для решения однородного уравнения (15) используется его алгебраизация, основанная на свойстве дифференцирования экспоненциальной функции. При Х = еrt уравнение (15) принимает вид:
(an rn + an-1 rn-1 + . . . + a1 r + a0 ) ert = 0
Это равенство удовлетворяется, если
an rn + an-1 rn-1 + . . . + a1 r + a0 = 0 (16)
т. е. задача сводится к отысканию корней уравнения (16), которое называется характеристически. Если все корни r1, r2, . . . , ri, . . . , rn характеристического уравнения разные, то каждому из них соответствует решение Xi = еrit однородного уравнения (15). Общее решение в этом случае

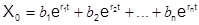
где коэффициенты b1,b2, . . . , bn — произвольные постоянные.
Если какой-нибудь корень характеристического уравнения ri является корнем k-й кратности, то
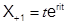 ;
; 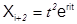 ; . . . ;
; . . . ; 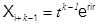
тоже служат решениями однородного уравнения (15). Общим решением уравнения (15) в этом случае служит линейная комбинация
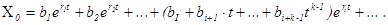
Наконец, если среди корней есть комплексные (они могут быть только попарно сопряженными при действительных коэффициентах аi), например, если ri = a + jb; r2 =-jb , то в соответствующих членах общего решения функции 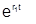 и
и 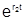 должны быть заменены на еatcosbt и еatsinbt. Получающиеся при этом выражения вида b1cosbt + b2sinbt могут быть представлены в виде Acos(bt +j).
должны быть заменены на еatcosbt и еatsinbt. Получающиеся при этом выражения вида b1cosbt + b2sinbt могут быть представлены в виде Acos(bt +j).
Частное решение уравнения (14) зависит от вида функции Q(t).
Пример 36. Решить уравнение динамики, составленное в предыдущем примере.
Решение. Характеристическое уравнение, соответствующее однородному уравнению
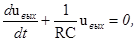
имеет вид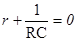 .Единственный корень этого уравнения
.Единственный корень этого уравнения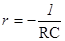 ,поэтому общее решение однородного уравнения
,поэтому общее решение однородного уравнения 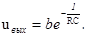
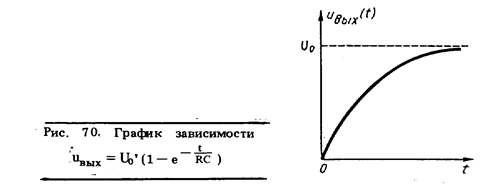
Частное решение неоднородного уравнения динамики, составленного в предыдущем примере, найдем исходя из того, что при 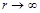 оно должно соответствовать установившемуся режиму. В установившемся режиме конденсатор окажется заряженным до напряжения u0, т.е.при
оно должно соответствовать установившемуся режиму. В установившемся режиме конденсатор окажется заряженным до напряжения u0, т.е.при 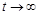
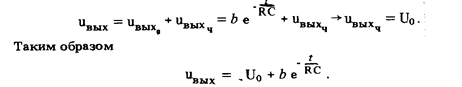
Постоянная интегрирования b находится из начальных условий. Так как энергия, запасенная в конденсаторе, не может в момент времени t = 0 измениться скачком от 0 до 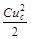 , uвых будет плавно нарастать от 0 до u0 . Это возможно только при b = - u0 . Поэтому окончательно
, uвых будет плавно нарастать от 0 до u0 . Это возможно только при b = - u0 . Поэтому окончательно
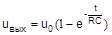
График полученной зависимости представлен на рис. 70.
Операторный метод решения уравнения д и н а м и к и. При сложных функциях Q(t) отыскание частного решения уравнения (14) превращается в проблему. В этих случаях пользуются операторным методом решения уравнения динамики.
Идея операторного метода, предложенного в конце XIX века английским инженером Хевисайдом для расчета переходных процессов в электрических цепях,состоит в алгебраизации уравнения динамики, которая достигается путем перехода от временных зависимостей к зависимостям от комплексного параметра р = a + jw посредством интегрального преобразования Лапласа:

С учетом этих соотношений дифференциальное уравнение динамики (14) при нулевых начальных условиях преобразуется в алгебраическое
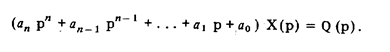
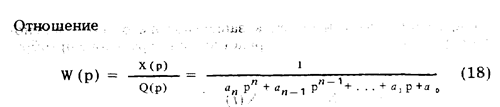
называется передаточной функцией. Как и уравнение (14), передаточная функция характеризует инерционные свойства средства измерений и может использоваться для изучения переходного режима его работы.
Зная передаточную функцию W(p) и изображение входного воздействия на средство измерений Q (р), можно по формуле
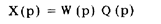
найти изображение отклика средства измерений на это входное воздействие, после чего, применив обратное преобразование Лапласа
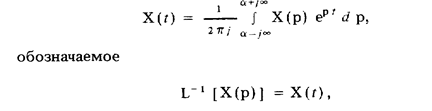 |
перейти к оригиналу Х(t), т. е. найти сам отклик.
Пример 37. Решить уравнение динамики, составленное в примере 33, операторным методом.
Решение*. 1. Применив преобразование Лапласа к левой и правой частям уравнения, перейдем к его алгебраической форме:
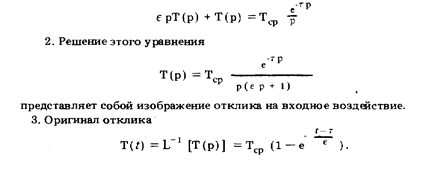
Спектральный метод решения уравнения динамики. При некоторых видах входных воздействий для алгебраизации уравнения динамики удобнее пользоваться не преобразованием Лапласа, а преобразованием Фурье:
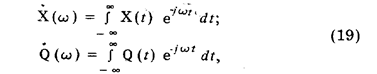
где Х(w) и Q(w) — комплексные спектры соответственно отклика X(t) и входного воздействия Q(t). Операция (19) называется прямым преобразованием Фурье и обозначается
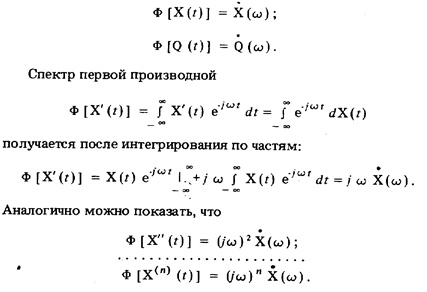
С учетом этих соотношений дифференциальное уравнение динамики (14) преобразуется в алгебраическое
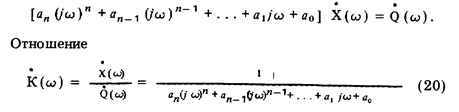
называется комплексным коэффициентом преобразования (передачи). Как и передаточная функция, комплексный коэффициент преобразования характеризует инерционные свойства средства измерений и может использоваться для изучения переходного режима его работы. Модуль комплексного коэффициента преобразования K(w) называется амплитудно-частотной, а фаза j (w) — фазочастотной характеристиками.
Зная комплексный коэффициент преобразования 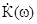 и комплексный спектр входного воздействия
и комплексный спектр входного воздействия 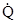 (w), можно по формуле
(w), можно по формуле
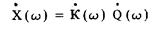
найти комплексный спектр отклика средства измерений на это входное воздействие, после чего, применив обратное преобразование Фурье
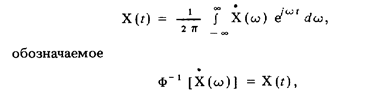
определить сам отклик.
Пример 38. Решить уравнение динамики, составленное в примере 34, спектральным методом.
Решение. 1. Применив преобразование Фурье к левой и правой частям уравнения, перейдем к его алгебраической форме:
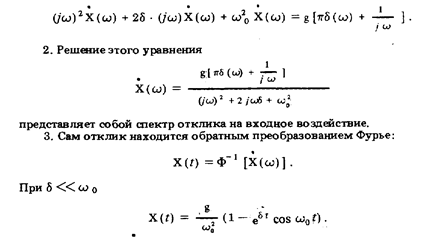
Обратная задача динамики. До сих пор мы рассматривали входное воздействие Q (t) в виде так называемой ступени. На практике зависимость измеряемой величины от времени может быть гораздо более сложной. Задача измерения состоит в определении этойнеизвестной зависимости Q (t) по зарегистрированному отклику на нее Х (t) посредством решения уравнения (14). Такая задача называется обратной задачей динамики.
В общем случае обратная задача динамики не имеет решения. Очень часто, например, в отклике Х(t) -не содержится всей необходимой информации о Q (t), потому что высокочастотные составляющие входного воздействия отфильтрованы вследствие инерционных свойств средства измерений, и информация о них безвозвратно потеряна. Однако в некоторых случаяхпри наличии определенно априорной информации о Q (t)обратная задача динамики может быть решена.
Так, в частности, на основе априорных сведений о Q (t) иногда можно подобрать такую зависимость Q (t), при которой отклик на нее средства измерений с достаточной степенью точности совпадает с откликом на Q (t).Q (t) в этом случае принимается за результат измерения.
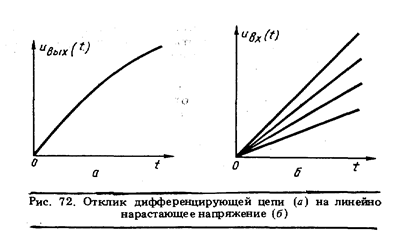
Пример 39. Отклик дифференцирующей цепи (рис. 71) на линейно нарастающее напряжение представлен на рис. 72 а. Определить входное воздействие.
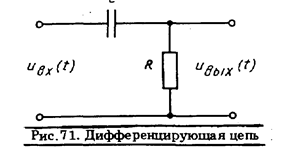
Решение методом замещения. Если имеется такая возможность, то на вход дифференцирующей цепи подаются линейно нарастающие напряжения различной крутизны (рис. 72, б), и из них выбирается такое ивх(t), отклик на которое с требуемой точностью совпадает с представленным на рис. 72, а. Это Uвх(t) с выбранной точностью принимается за результат измерения.
Решение расчетным путем. 1. Составим уравнение динамики. Согласно второму закону Кирхгофа
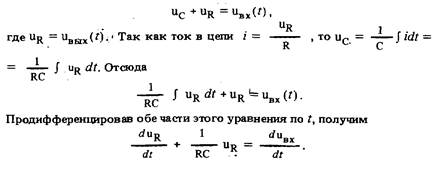
2. Решение уравнения динамики операторным методом. В операторной форме уравнение динамики имеет вид:
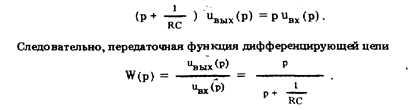
Согласно априорной информации входное воздействие uвх(t) = at, где неизвестный постоянный коэффициент а определяется посредством измерения.
Изображение входного воздействия (см. табл. 19)
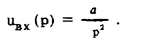
Изображение отклика дифференцирующей цепи на линейно нарастающее входное воздействие
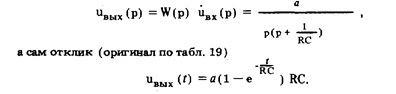
В этом уравнении с одним неизвестным а подбирается таким, чтобы Uвых(t) c требуемой точностью совпало с представленным на рис. 72, а.
В некоторых случаях отклик средства измерений внешне не имеет ничего общего с входным воздействием, однако при наличии достаточного объема априорной информации позволяет решить измерительную задачу.
Пример 40. Отклик дифференцирующей цепи, рассмотренной в примере 39, на трапецеидальный импульс представлен на рис. 73 а. Определить входное воздействие.
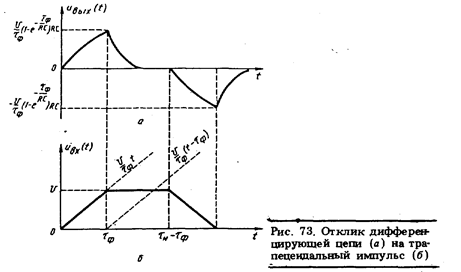
Решение. Согласно априорной информации на участке, соответствующем переднему фронту трапецеидального импульса

Аналогично (при ненулевых начальных условиях) решается уравнение динамики для заднего фронта трапецеидального импульса.
График на рис. 73, б представляет окончательное решение задачи. Сравнивая рис. 73, б и рис. 73, а, можно заключить, что по графику на рис. 73, а определяются все параметры входного воздействия (трапецеидального импульса).
Приведенный пример показывает, что успешное решение обратной задачи динамики иногда достигается выбором специфического средства измерений (в данном случае дифференцирующего измерительного преобразователя).
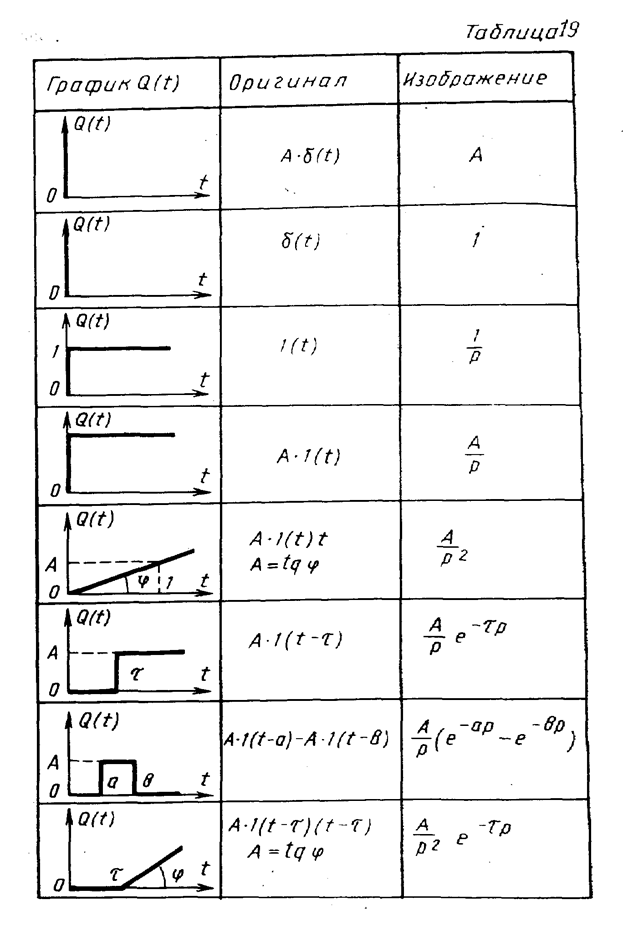
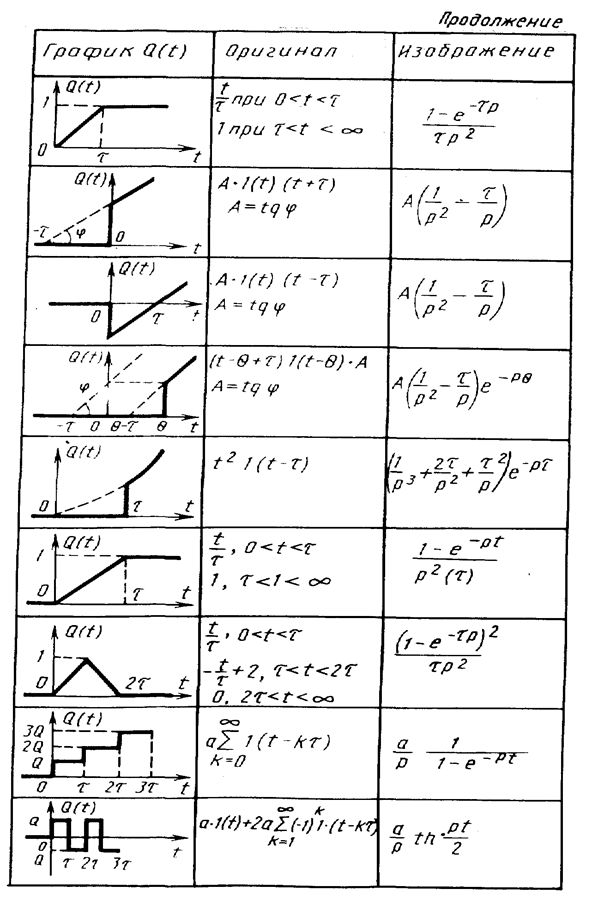
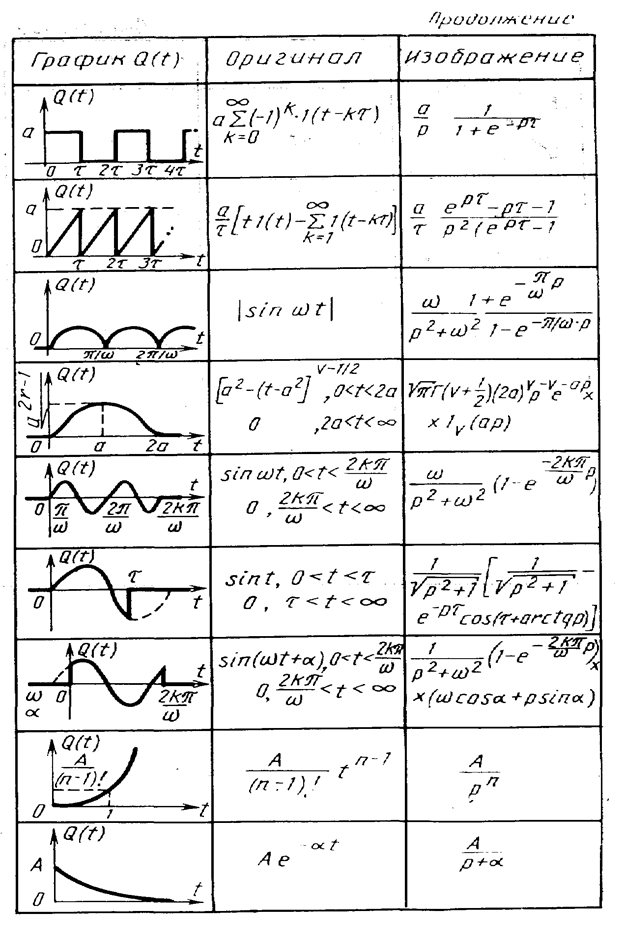
Решение измерительной задачи методом подбора входного воздействия предполагает использование различных его моделей. Сведения о некоторых из них приведены в табл. 19.
При сложных моделях входных воздействий отклики на них рассчитываются методом интеграла Дюамеля. Сущность этого метода заключается в следующем.
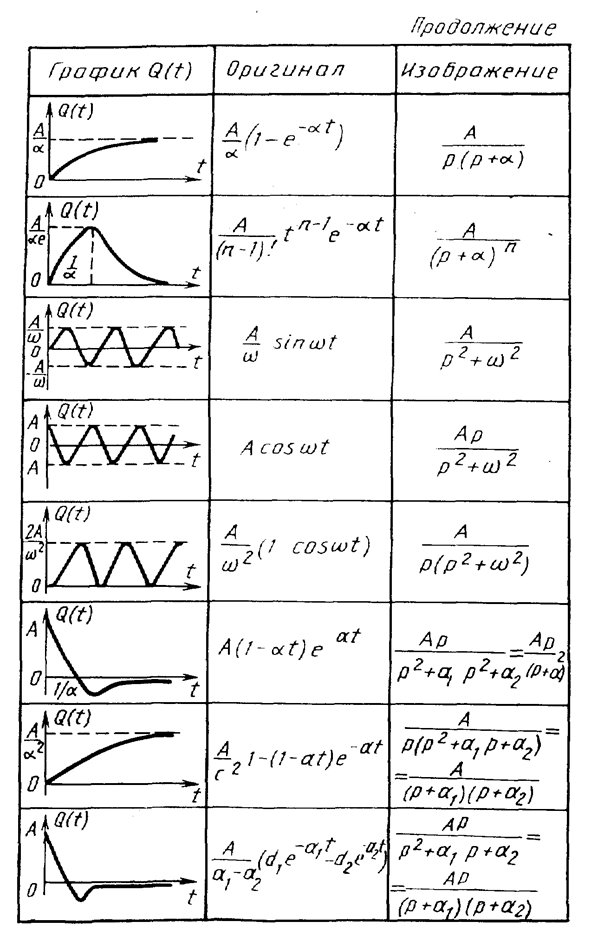
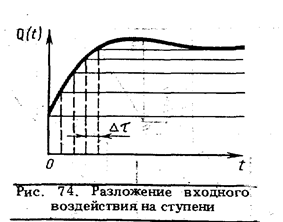
Сложное входное воздействие (см. рис. 74) рассматривается как сумма начальной ступени Q (0) · 1(t) и следующих через равные промежутки времени Dt маленьких ступеней, величина которых DQ(n × Dt) »Dt × Q'(n × Dt).
Ранее уже использовалось в решении примеров 37, 39 приведенное в табл. 19 входное воздействие в виде единичной ступени
Отклик h (t) средства измерений на такое входное воздействие называется переходной характеристикой. Так же как уравнение динамики, передаточная функция и комплексный коэффициент преобразования переходная характеристика отражает инерционные свойства средства измерений.
Отклик средства измерений на каждую n-ю ступень, показанную на рис. 74, равен величине этой ступени, умноженной на h (t - n× Dt). В соответствии с принципом суперпозиции (наложения), справедливым для линейных систем, в каждый дискретный момент времени t = k × Dt отклик средства измерений определяется как сумма откликов на все предшествующие ступени:
Переходя к пределу при n® ¥ и Dt ®0, получим одну из форм так называемого интеграла Дюамеля (интеграла наложения):
С помощью несложных преобразований можно получить и другие его формы:
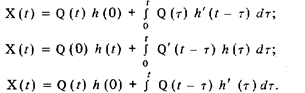
При расчетах выбирается та из них, подынтегральная функция у которой проще.
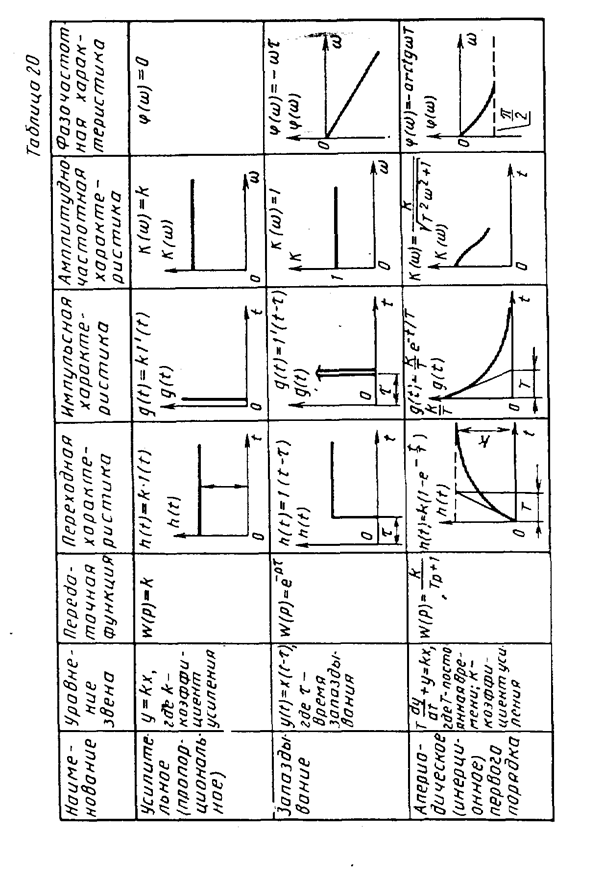
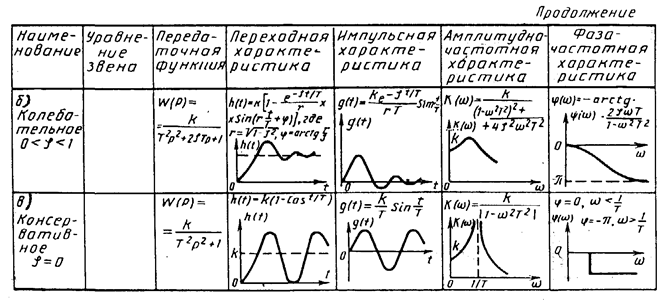
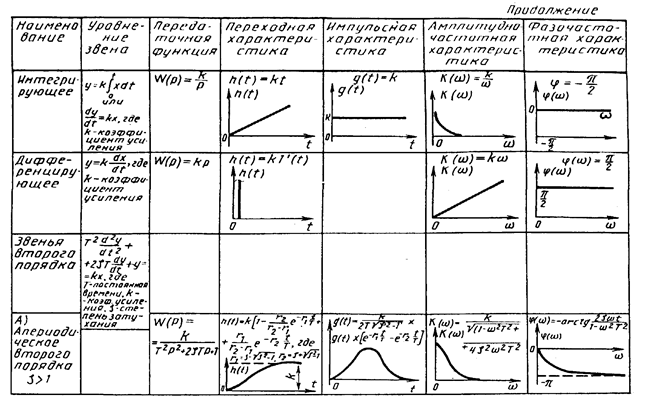
Типовые динамические звенья. Любое средство измерений при анализе его инерционных свойств можно представить в виде совокупности определенным образом связанных между собой элементарных динамических звеньев. Под динамическим звеном понимается устройство любого физического вида и конструктивного оформления, работа которого описывается определенным уравнением, т. е. каждое звено обладает характерными для него динамическими свойствами. Одним и тем же уравнением может описываться работа самых разнообразных устройств (механических, электрических, тепловых и др.), но все они в этом случае будут относиться к динамическому звену одного и того же типа. Такие звенья принято называть типовыми. Математическое описание и характеристики инерционных свойств типовых звеньев приведены в табл.20.
В число характеристик средств измерений, определяющих их инерционные свойства, в табл. 20 включена импульсная характеристика g(t), представляющая собой отклик средства измерений на единичный импульс
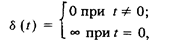
называемый так потому, что площадь, ограниченная, этой функцией, равна 1. Как видно из табл. 20,единичный импульс есть ни что иное как первая производная от единичной ступени. Иногда он называется дельта-функцией или функцией Дирака.
Все многообразие структурных схем средств измерений может быть представлено с помощью трех вариантов соединения типовых динамических звеньев: последовательного, параллельного и с обратной связью.
Последовательным называется такое соединение звеньев, при котором отклик предыдущего звена является входным воздействием для последующего (см. рис. 75).

Система уравнений, описывающая работу средства измерений, имеет вид:
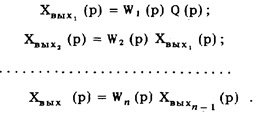
Решение этой системы относительно изображений отклика и входного воздействия:
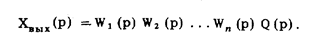
Таким образом, передаточная функция последовательного соединения звеньев равна произведению их передаточных функций:
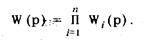
Параллельным называется такое соединение звеньев, при котором входное воздействие является общим для всех звеньев, а отклики на него суммируются (см. рис. 76).
Работа средства измерений, состоящего из параллельно соединенных динамических звеньев, описывается системой уравнений:
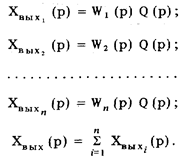
Решение этой системы уравнений относительно изображений входного воздействия и отклика на него средства измерений имеет вид:
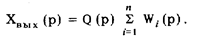
Таким образом, передаточная функция параллельного соединения звеньев равна сумме их передаточных функций:
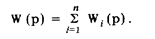
Соединением с обратной связью называется такое соединение, при котором отклик первого звена является одновременно откликом соединения и входным воздействием второго звена, а  отклик второго звена, алгебраически суммируясь с измеряемой величиной, образует входное воздействие первого звена (см. рис. 77). Суть обратной связи заключается в том, что преобразованный вторым звеном отклик либо усиливает, либо ослабляет входное воздействие на первое звено.
отклик второго звена, алгебраически суммируясь с измеряемой величиной, образует входное воздействие первого звена (см. рис. 77). Суть обратной связи заключается в том, что преобразованный вторым звеном отклик либо усиливает, либо ослабляет входное воздействие на первое звено.
В первом случае обратная связь называется положительной, во втором —отрицательной.
Работа соединения звеньев с обратной связью описывается системой уравнений:
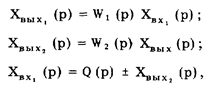
где знак плюс в последнем уравнении соответствует положительной обратной связи, а знак минус — отрицательной. Отрицательную обратную связь на схемах принято обозначать зачерненным сектором в суммирующем элементе  .
.
Решение последней системы уравнений:

где уже знак минус соответствует положительной обратной связи, а знак плюс — отрицательной.
Передаточная функция
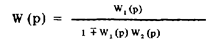
В общем случае передаточная функция соединения с обратной связью представляет собой дробь, числитель которой равен передаточной функции звеньев, расположенных между точками входного воздействия и отклика на него, а знаменатель — увеличенному на единицу произведению передаточных функций всех звеньев соединения.
Пример 41. Структурная схема соединения динамических звеньев приведена на рис. 78, а. Определить передаточную функцию устройства.
Решение. Представим структурную схему в упрощенном виде — см. рис. 78,б, где
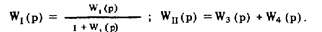
Для последовательного соединения звеньев, охваченного отрицательной обратной связью,
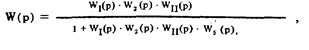
Теорема разложения. В подавляющем большинстве случаев передаточная функция средства измерений является дробью, из чего следует, что дробью является и изображение отклика средства измерений, от которого посредством обратного преобразования Лапласа нужно перейти к оригиналу. Данных, приведенных в табл. 19, может оказаться для этого недостаточно. Поэтому широкое применение получила так называемая теорема разложения, сформулированная Хевисайдом. Согласно этой теореме изображение в виде правильной рациональной дроби может быть разложено на простые дроби, оригиналы для которых известны из табл. 19. Оригинал отклика .в этом случае равен сумме оригиналов изображений в виде простых дробей.
Предположим, что изображение отклика имеет вид дроби
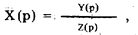
где Y (р) и Z (р) — степенные полиномы, причем степень полинома Y (р) меньше степени n полинома Z (р). Если найти корни ai, уравнения Z (р) = 0, то указанную дробь можно единственным образом представить в виде суммы простейших правильных дробей. Подобное представление известно в математике как разложение на простые дроби. При различных вещественных корнях ai члены разложения имеют вид 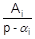 и, в частности,
и, в частности, 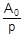 при a0 = 0, где Аi — постоянные вещественные коэффициенты. Каждому из комплексных корней соответствует дробь того же вида, но коэффициенты ее не являются вещественными. Чтобы избежать операций с комплексными числами, выделяют элементарные дроби вида
при a0 = 0, где Аi — постоянные вещественные коэффициенты. Каждому из комплексных корней соответствует дробь того же вида, но коэффициенты ее не являются вещественными. Чтобы избежать операций с комплексными числами, выделяют элементарные дроби вида 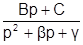 , соответствующие паре комплексно-сопряженных корней. Таким образом, в общем случае изображение отклика можно представить следующей суммой простых дробей:
, соответствующие паре комплексно-сопряженных корней. Таким образом, в общем случае изображение отклика можно представить следующей суммой простых дробей:
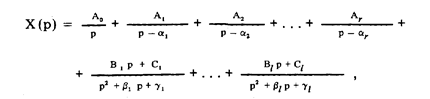
где ¡ + 21 + 1 = п. Для определения коэффициентов Ао, A1, . . . , Ar, B1, C1, . . . , Bl, Cl существует несколько способов. Достаточно просто эти коэффициенты определяются известным в математике методом неопределенных коэффициентов.

Пример 42. Изображение отклика средства измерений на входное воздействие
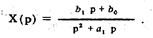
Найти оригинал отклика, используя теорему разложения.
Решение. 1. Корни уравнения р2 + a1p = 0 вещественные: a0 = 0; a1 = - a1
2. Разложение изображения отклика на простые дроби имеет вид:
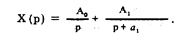
3. Для определения ао и A1 воспользуемся методом неопределенных коэффициентов. Приравнивая друг к другу два выражения для Х (р), получим:

Дата добавления: 2015-02-05; просмотров: 2140;
