Установившийся режим
В примерах, показанных на рис. 56, 57, 59, 60, 63, 64, указатель отсчетного устройства останавливается на одной из отметок шкалы спустя некоторое время t после начала измерения физической величины постоянного размера. У показывающих измерительных приборов это время называется временем установления показания, а режим работы средств измерений после установления показания — установившимся режимом. В установившемся режиме отметкам шкалы отсчетного устройства соответствуют определенные значения измеряемой величины. Это позволяет связать положение указателя в установившемся режиме с неизвестным значением измеряемой величины.
У измерительных преобразователей реакция на входное воздействие называется откликом, или выходным сигналом. Это может быть изменение угла поворота стрелки у приборов, показанных на рис. 56, 57, 59, 60, изменение длины столба термометрической жидкости (в примере, показанном на рис. 63), перемещение стрелочного указателя динамометра (в примере на рис. 64) и т. п. Время установления выходного сигнала называется временем реакции средства измерений. Зависимость между входным воздействием и откликом на него измерительного преобразователя, а также измерительного прибора с неименованной шкалой или со шкалой, отградуированной в единицах, отличных от единиц входной величины, называется функцией преобразования.В установившемся режиме функция преобразования представляет собой линейное (например, Х = aQ — см. рис. 65, а)или нелинейное (например, Х = aQ2 — см. рис. 65, б или Х = a lg Q — рис. 65, в)алгебраическое уравнение статики.
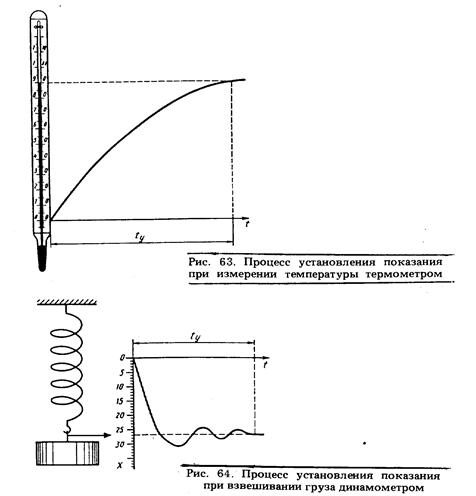 Как отмечалось в разд. 4.3.2, функция преобразования, принимаемая для всех средств измерений данного типа, называется номинальной. Конкретный экземпляр средства измерений имеет индивидуальную функцию преобразования, несколько отличающуюся от номинальной. Нередко поэтому в нормативно-технических документах на средства измерений нормируются пределы, в которых находится их индивидуальная функция преобразования. Линейную функцию преобразования, проходящую через начало координат, допускается представлять коэффициентом преобразования в виде числа. В этом случае нормируются пределы, в которых находится его значение.
Как отмечалось в разд. 4.3.2, функция преобразования, принимаемая для всех средств измерений данного типа, называется номинальной. Конкретный экземпляр средства измерений имеет индивидуальную функцию преобразования, несколько отличающуюся от номинальной. Нередко поэтому в нормативно-технических документах на средства измерений нормируются пределы, в которых находится их индивидуальная функция преобразования. Линейную функцию преобразования, проходящую через начало координат, допускается представлять коэффициентом преобразования в виде числа. В этом случае нормируются пределы, в которых находится его значение.
Пример 31. Номинальная функция преобразования измерительного преобразователя в установившемся режиме представлена на рис. 65 а. Коэффициент преобразования аi, у отдельных экземпляров средств 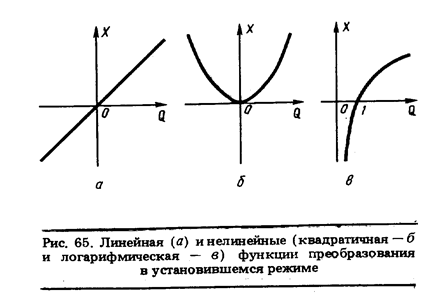 измерений этого типа не отличается от номинального больше, чем на 1 %. Что можно сказать о классе точности таких средств измерений?
измерений этого типа не отличается от номинального больше, чем на 1 %. Что можно сказать о классе точности таких средств измерений?
Решение. Выражения для номинальной и индивидуальной функций преобразования имеют, соответственно, вид:
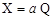
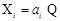
Вычитая первое уравнение из второго, получим
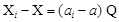
откуда 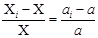
 По условию это отношение может достигать 0,01. Следовательно, класс точности таких измерительных преобразователей не может быть выше
По условию это отношение может достигать 0,01. Следовательно, класс точности таких измерительных преобразователей не может быть выше
Сведения о функции преобразования, содержащиеся в нормативно-технических документах, предназначены для использования в случаях, когда к точности измерений не предъявляется высоких требований. В противном случае может возникнуть необходимость уточнения индивидуальной функции преобразования конкретного экземпляра средств измерений. Процедура экспериментального определения функциипреобразования отдельного средства измерений в установившемся режиме называется градуировкой.
При градуировке средств измерений находится зависимость между известными входными воздействиями и откликами на них в установившемся режиме. Различают градуировку в отдельных точках диапазона измерений, при которой функция преобразования может быть представлена, например, таблицей, и построение градуировочной характеристики, которая аппроксимируется аналитическим выражением.
Градуировка в отдельных точках диапазона измерений сводится к обычной обработке экспериментальных данных. Так например, при градуировке ртутного термометра в двух реперных точках (при температуре таяния льда и температуре кипения воды) получают по п значений длины ртутного столба в каждой точке. Затем оба массива экспериментальных данных обрабатывают по правилам, изложенным в разд. 2. В результате с определенной точностью и достоверностью устанавливают, какой длине ртутного столба соответствует температура 0° С, и какой 100° С.
Построение градуированной характеристики предполагает две возможности. Первая из них заключается в том, что вид функции преобразования известен (линейная, квадратичная, логарифмическая и т. п.), но неизвестны коэффициенты, входящие в соответствующее алгебраическое уравнение. Вторая возможность состоит в необходимости аппроксимации экспериментальных данных аналитической зависимостью.
Если вид функции преобразования X=f(Q) известен, то задача состоит в том, чтобы в ее представлении полиномом соответствующей степени
f (Q) = ао + а1Q + а2Q2 +. . .+ аm Qm
найти такие значения коэффициентов a0, а1 , а2, . . . , am, при которых эта зависимость, называемая тогда уже градуировочной характеристикой, наилучшим образом соответствовала бы экспериментальным данным.
На рис. 66 показаны некоторые варианты построения линейной градуировочной характеристики по экспериментальным данным, нанесенным кружочками. Вопрос о том, какой из вариантов лучше, должен решаться на основе какого-то критерия. Если значения входных воздействий Q1, Q2,. . . ,Qn известны точно, а отклики на них подчиняются нормальному закону распределения вероятности, то обычно используется критерий наименьших квадратов (см. разд. 2.6.1). Минимизируется сумма квадратов отклонения откликов по оси ординат от градуировочной характеристики:
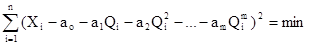
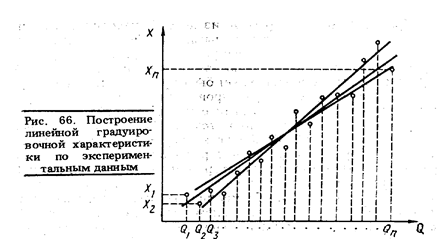
Коэффициенты ао, а1, а2, . . . , аm, .определяющие оптимальную по критерий наименьших квадратов градуировочную характеристику, находятся из условия равенства нулю производных от этой суммы по каждому коэффициенту.
Пример 32. При градуировке измерительного преобразователя с линейной функцией преобразования получены следующие числовые значения экспериментальных данных:
Найти методом наименьших квадратов. аналитическое выражение для градуировочной характеристики и построить ее графически.
Решение. 1. Линейная функция преобразования описывается выражением
Х=ао + а1Q
где коэффициенты ао и а1 методом наименьших квадратов находятся из условия
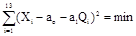
2. Вышеприведенная функция минимальна в точке, где ее производные по а0 и а1 равны нулю. Поэтому коэффициенты а0 и а1 определяются в результате решения системы уравнений
| Q, | X, |
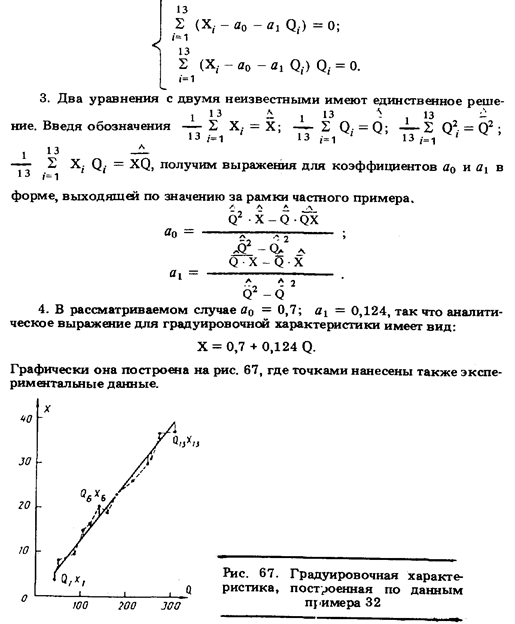
Выражения для коэффициентов а0 и а1, полученные в рассмотренном примере, иногда используются при градуировке измерительных преобразователей с нелинейной функцией преобразования. Так, например, если функция преобразования имеет вид
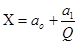
то введение новой переменной 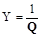 позволяет перейти к построению линейной градуировочной характеристики. Точно так же, если
позволяет перейти к построению линейной градуировочной характеристики. Точно так же, если
Х= а - bQ,
то для логарифма отклика градуировочная характеристика будет опять-таки линейной. Это существенно расширяет область применения выражений для а0 и а1, полученных в примере 32.
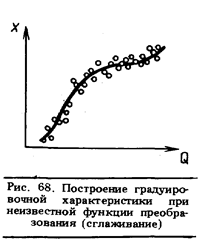 Если вид функции преобразования неизвестен, то возникает задача отыскания наилучшей аппроксимации экспериментальных данных, полученных при градуировке, аналитической зависимостью (см. рис. 68). Решение ее методом наименьших квадратов отличается от решения предыдущей задачи только тем, что степень полинома
Если вид функции преобразования неизвестен, то возникает задача отыскания наилучшей аппроксимации экспериментальных данных, полученных при градуировке, аналитической зависимостью (см. рис. 68). Решение ее методом наименьших квадратов отличается от решения предыдущей задачи только тем, что степень полинома
f (Q) = а0 + а1Q + а2Q2 + ...
неизвестна. Она устанавливается на основании требований к точности градуировки. После этого минимизируется выражение (13). Количество уравнений для определения коэффициентов а0, а1, а2,… всегда равно числу неизвестных, так что задача имеет единственное решение. В специальной литературе она иногда называется задачей сглаживания.
Дата добавления: 2015-02-05; просмотров: 1953;
