МАТЕМАТИЧЕСКИЕ ДЕЙСТВИЯ С НЕСКОЛЬКИМИ РЕЗУЛЬТАТАМИ ИЗМЕРЕНИЙ
Начнем со сложения результатов измерений.
Пример 90. Распределение вероятности числового значения результата измерения одной из сторон прямоугольника представлено табл. 54. Независимое измерение прилежащей стороны дало в точности такой же результат, т.е. прямоугольник является квадратом. Определить его полупериметр.
Решение. Полу периметр квадрата является величиной, значение которой равно сумме двух других значений r1 и r2; , каждое из которых задано распределением вероятности, представленным таблицей 54. По условию r1 = r2 = г. При r1 = 3 второе слагаемое r2 может иметь любое из трех числовых значений, приведенных в табл. 54. Вероятность того, что r1 + r2 = 3 + 3 = 6, равна 0,2 • 0,2 = 0,04; вероятность того, что r1 + r2 = 3 + 4 = 7, составляет 0,2 • 0,5 = 0,10; вероятность того, что r1 + r2 = 3 + 5 = 8, определяется таким же образом: 0,2 • 0,3 = 0,06. Аналогичные варианты возникают при r1 = 4 и r1 = 5. Все они сведены в табл. 55.
Таблица 55
| r1 | r2 | r1 + r2 | P=P1 P2 |
| 0,2 • 0,2 = 0,04 | |||
| 0,2 • 0,5 = 0,10 | |||
| 0,2 • 0,3 = 0,06 | |||
| 0,5 • 0,2 = 0,10 | |||
| 0,5 • 0,5 = 0,25 | |||
| 0,5 • 0,3 = 0,15 | |||
| 0,3 • 0,2 = 0,06 | |||
| 0,3 • 0,5 = 0,15 | |||
| 0,3 • 0,3 = 0,09 |
Из табл. 55 видно, что
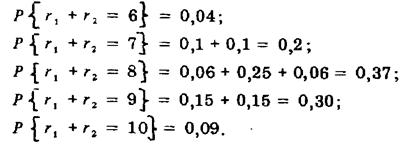
Таким образом числовое значение полупериметра как суммы значении двух прилежащих сторон, полученных путем независимого измерения последних, подчиняется следующему распределению вероятности:
r1 + r2 Р
6 0,04
7 0,20
8 0,37
9 0,30
10 0,09
На рис. 194 распределения вероятности числовых значений полупериметра и сторон квадрата представлены графически. Далее
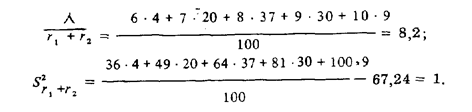
Таким образом, для оценок, как и для самих числовых характеристик, среднее арифметическое суммы независимых результатов измерений
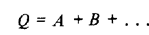
равно сумме их средних арифметических:
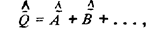
а квадрат стандартного отклонения — сумме квадратов стандартных отклонений:
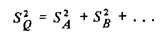
Стандартное отклонение среднего арифметического значения периметра
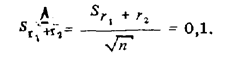
Согласно неравенству П.Л. Чебышева с вероятностью не менее 0,9
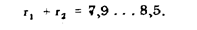
Пример 91. В табл. 56 приведено 100 независимых значений результата взвешивания консервированного продукта вместе со стеклянной банкой и крышкой mб (брутто), в табл. 57 — только банки и крышки (тары).
Таблица 56
| mб , кг | m | Pб |
| 3,98 | 0,3 | |
| 4,00 | 0,5 | |
| 4,03 | 0,1 | |
| 4 04 | 0,1 |
Таблица 57
| mT , кг | m | PT |
| 0,88 | 0,2 | |
| 0,90 | 0,7 | |
| 0,93 | 0,1 |
Определить массу консервированного продукта тH (нетто).
Решение. Масса консервированного продукта mH равна разности двух результатов измерений
mH= mб – mт ,
распределения вероятности которых заданы таблично. По тому же принципу, по которому составлена табл. 65, составим табл. 58.
Таблица 58
| mб,кг | mт, кг | mН, кг | РН =РбРТ | mб,кг | mT, кг | mH, кг | РН=Рб РТ |
| 3,98 | 0,88 | 3,10 | 0,3×0,2 =0,06 | 4,03 | 0,88 | 3,15 | 0,1×0,2= 0,02 |
| 3,98 | 0,90 | 3,08 | 0,3×0,7 =0,21 | 4,03 | 0,90 | 3,13 | 0,1×0,7 = 0,07 |
| 3,98 | 0,93 | 3,05 | 0,3×0,1 =0,03 | 4,03 | 0,93 | 3,10 | 0,1×0,1 = 0,01 |
| 4,00 | 0,88 | 3,12 | 0,5×0,2 =0,10 | 4,04 | 0,88 | 3,16 | 0,1×0,2 = 0,02 |
| 4 00 | 0,90 | 3,10 | 0,5×0,7 =0,35 | 4,04 | 0,90 | 3.14 | 0,1×0,7 = 0,07 |
| 4,00 | 0,93 | 3,07 | 0,5×0,1 =0,05 | 4,04 | 0,93 | 3,11 | 0,1×0,1 = 0,01 |
По данным табл. 58 распределение вероятности массы консервированного продукта можно представить следующим образом:
mH, кг РН mH, кг РН
3,05 0,03 3,12 0,10
3,07 0,05 3,13 0,07
3,08 0,21 3,14 0,07
3,10 0,42 3,15 0,02
3,11 0,01 3,16 0,02
или графически, как показано на рис. 197. Оценки числовых характеристик теоретической модели, соответствующей этому эмпирическому распределению вероятности
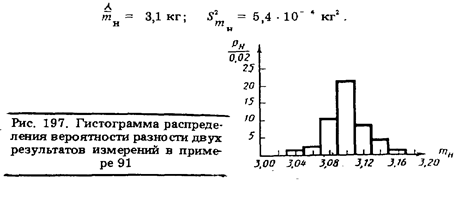
Так как эмпирическим распределением вероятности, представленным табл. 56 и 67, соответствуют
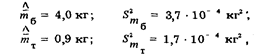
то действительно среднее арифметическое разности независимых результатов измерений
Q= A - В
равно разности их средних арифметических:
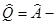
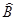 ,
,
а квадрат стандартного отклонения — сумме квадратов стандартных отклонений:
S 2Q = S 2A + S 2B .
На этом основании, принимая во внимание, что
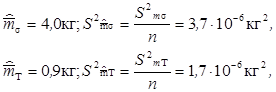
можно было бы получить
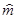 H =
H = 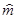
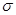 -
- 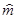 T = 3,1 кг ;
T = 3,1 кг ;
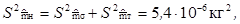
что соответствует результату, который вытекает непосредственно из оценок числовых
характеристик теоретической модели эмпирического распределения вероятности, представленного на с. 470. Судя по гистограмме, mH подчиняется нормальному закону распределения вероятности (что можно проверить по критерию К. Пирсона) . Следовательно, нормальному закону подчиняется и тH. Поэтому с вероятностью 0,95 масса консервированного продукта
т = 3,095 . . . 3,105 кг.
Из сравнения распределений вероятности Р (r + r) и Р (2r) на рис. 194 и оценок дисперсий S 2r+r , S 22r в примерах 84 и 90 видно,что
r+r 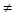 2r , или в общем случае
2r , или в общем случае
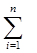 Qi
Qi 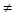 nQ ,
nQ ,
где Qi = Q.
Игнорирование этого обстоятельства приводит к ошибкам Например, с вероятностью 0,95 масса 10000 банок консервов рассмотренных в примере 91, вычисленная по аддитивному алгоритму, составляет (40000 ± 0,4) кг, а по мультипликативному - (40000 ± 40) кг. Нельзя рассчитывать по мультипликативному алгоритму электрическое сопротивление цепи состоящей из нескольких одинаковых сопротивлений, соединенных последовательно между собой; суммарную электрическую емкость параллельного соединения нескольких одинаковых конденсаторов и т.д., если числовые значения соответствующих величин заданы или определены как случайные числа. В равной мере нельзя заменять суммированием умножение случайного числа на неслучайный постоянный множитель. Например, вес товарной партии консервов, рассмотренной выше, с вероятностью 0,95 составляет примерно (4 × 105 ± 4) Н,а не (4 ×105 ± 1) Н.
Закон распределения вероятности суммы независимых результатов измерений называется композицией законов распределения вероятности слагаемых. Для определения композиции различных законов распределения вероятности результатов измерений широко используется метод характеристических функции.
Характеристической функцией случайной величины Q называется математическое ожидание случайной величины e j 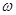 Q ,где w - неслучайный параметр. Если Q — сумма независимых результатов измерений А, В, . . . то
Q ,где w - неслучайный параметр. Если Q — сумма независимых результатов измерений А, В, . . . то
М (e jwQ) =М (e jwA ×e jwB ....),
где сомножители так же независимы, как и результаты измерений. Поэтому
М (e jwQ) =M (e jwA) ×M (e jwB) .....
Если характеристическую функцию определить как спектр плотности распределения вероятности результата измерения:
M (e – jwQ) = 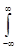 e – jwQ pQ (Q) d Q = pQ (w), то
e – jwQ pQ (Q) d Q = pQ (w), то
PQ (w) = 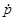 A (w)
A (w) 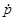 B (w) . . . . ,
B (w) . . . . ,
то естьспектр плотности распределения вероятности суммы независимых результатов измерений равен произведению спектров плотности распределения вероятности слагаемых.
Плотность распределения вероятности композиции нескольких законов распределения независимых результатов измерений находится обратным преобразованием Фурье:
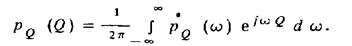
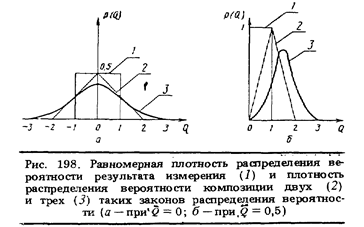
Пользуясь методом характеристических функций, можно показать, что композицией одинаковых равномерных законов распределения вероятности, которым подчиняются два независимых результата измерений, является треугольный закон (рис. 198), называемый законом распределения вероятности Симпсона. Композицией двух равномерных законов распределения вероятности независимых результатов измерений с неодинаковым размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации.
Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что, независимо от вида сомножителей, оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 198 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых, больше 4-х, уже можно считать, что она практически подчиняется нормальному закону.
На практике с распределениями вероятности результатов измерений оперируют только при очень точных вычислениях. Обычно ограничиваются расчетами на уровне оценок числовых характеристик.
Пример 92. При однократном взвешивании продукта в таре, рассмотренной в примере 91, на противоположную чашу настольных циферблатных весов поставлены две гири по (2 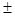 0,01) кг. Стрелочный указатель весов остановился на отметке шкалы 300 г. Определить массу продукта ту, если известно, что показание весов подчиняется нормальному закону распределения вероятности со средним квад-ратическим отклонением 5 г.
0,01) кг. Стрелочный указатель весов остановился на отметке шкалы 300 г. Определить массу продукта ту, если известно, что показание весов подчиняется нормальному закону распределения вероятности со средним квад-ратическим отклонением 5 г.
Решение. 1. По стрелочному указателю (без учета массы гирь и тары) масса продукта с вероятностью 0,95 находится в пределах ( 300 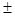 10) г. Представим эту ситуацию равномерным законом распределения вероятности на интервале от 290 г до 310 г со средним значением и аналогом дисперсии, равными соответственно
10) г. Представим эту ситуацию равномерным законом распределения вероятности на интервале от 290 г до 310 г со средним значением и аналогом дисперсии, равными соответственно
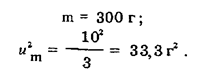
2. Чему равна масса каждой гири в интервале от 1,99 кг до 2,01 кг, неизвестно. Представим и эту ситуацию математической моделью в виде равномерного закона распределения вероятности на интервале от 1,99 кг до 2,01 кг со средним значением и аналогом дисперсии
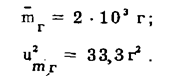
3. С учетом массы гирь и тары масса продукта будет представлена математической моделью в виде закона распределения вероятности со средним значением и аналогом дисперсии
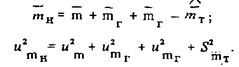
В данном случае неслучайное значение массы продукта mH 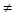
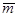 H т.к. ситуационная модель не подчиняется статистическим закономерностям, а учитывает недостаток (дефицит) информации. В соответствии с рекомендацией Международного комитета мер и весов (см. п. 2.5) примем
H т.к. ситуационная модель не подчиняется статистическим закономерностям, а учитывает недостаток (дефицит) информации. В соответствии с рекомендацией Международного комитета мер и весов (см. п. 2.5) примем
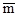 H – kumH
H – kumH 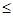 mH
mH 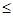
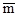 H + kumH
H + kumH
где значение коэффициента k устанавливается по согласованию. Положив, как и раньше, k = 2 и проведя вычисление

Подобные вычисления широко используются при внесении аддитивных поправок, точные значения которых неизвестны.
Умножение двух результатов измерений один на другой рассмотрим на примере, когда они равны между собой.
Пример 93. Определить площадь квадрата по данным, приведенным в примере 90.
Решение. Площадь квадрата s равна произведению его сторон
s = r1 × r2 ,
распределение вероятности числовых значений каждой из которых представлено табл. 54. По тому же принципу, по которому составлены табл. 55 и 58, составим таблицу 59.
Таблица 59
| r1 | r2 | S | P = P1 P2 | |
| 3 | 0,2 × 0,2 = 0,04 | |||
| 0,2 × 0,5 = 0,10 | ||||
| 0,2 × 0,3 = 0,06 | ||||
| 0,5 × 0,2 = 0,10 | ||||
| 0 5 × 0,5 = 0,25 | ||||
| 0,5 × 0,3= 0,15 | ||||
| 0,3 × 0,2 = 0,06 | ||||
| 0,3 × 0,5 = 0,15 | ||||
| 0,3 - 0,3 = 0,09 | ||||
Используя данные табл. 59, распределение вероятности площади квадрата можно представить следующим образом:
s Р
9 0,04
12 0,20
15 0,12
16 0,25
20 0,30
25 0,09
Оценка среднего значения теоретической модели этого эмпирического распределения
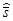 = 16,8 ,
= 16,8 ,
а стандартное отклонение
SS = 4,1 .
Сравнивая этот результат с результатом, полученным в примере 85, убеждаемся, что
r • r 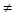 r2 ,
r2 ,
или в общем случае
п
П Qi 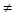 Qn , где Qi,= Q .
Qn , где Qi,= Q .
1
Игнорирование этого обстоятельства приводит к еще более серьезным ошибкам, чем при замене аддитивного алгоритма мультипликативным, или наоборот.
Стандартное отклонение среднего арифметического значения площади квадрата
S 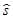 = 0,41.
= 0,41.
Так как закон распределения вероятности среднего арифметического неизвестен, воспользуемся неравенством П.Л. Чебышева: с вероятностью не менее 0,9
s = 16,5... 17,1.
Сопоставляя результат, полученный в последнем примере, с исходными данными в примере 84, видим, что оценки математических ожиданий обладают таким же свойством, как и сами математические ожидания:среднее арифметическое произведения нескольких независимых результатов измерений равно произведению их средних арифметических
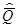 =
= 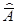 •
• 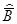 • …
• …
Характеристика рассеяния произведения связана с характеристиками рассеяния сомножителей более сложной зависимостью, которая будет рассмотрена позже.
На основании рассмотренных примеров 90, 91 и 93 можно заключить, что если
Q = f (A,B,...),
где независимые результаты измерений А, В, . . . заданы эмпирическими законами распределения вероятности, полученными с помощью цифровых измерительных приборов, то распределение вероятности
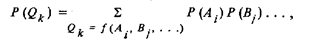
где суммируются только те произведения Р(Аi) Р (Bj) . . . , для которых f (Ai ,Bj , ...)= Qk .
Если результаты измерений А, В,... заданы теоретическими моделями эмпирических законов распределения вероятности, то следует опять-таки воспользоваться тем, что интегральная функция распределения вероятности F (Q) представляет собой вероятность того, что
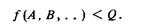
Это неравенство в многомерном пространстве выполняется для -всех. точек с координатами А, В, . . . , геометрическим местом которых является область G, ограниченная гиперповерхностью
f (A,B,...) = Q .
Поэтому через плотность совместного распределения вероятности результатов измерений р (А, В, . . .) интересующая нас вероятность выражается следующим образом:
F(Q)= ò …G ò p(A,B,…) dA dВ ... .
Если результаты измерений А, В, . . . независимы, то
F(Q) =ò …G ò pA (A) pB (B) ... dA dB ... . (55)
Пример 94. Найти плотность распределения вероятности суммы двух независимых результатов измерения А и В, первый из которых подчиняется нормированному нормальному закону, а второй — равномерному закону распределения вероятности на интервале (-1,1).
Решение. 1. Интегральная функция распределения вероятности F (Q) композиции двух рассматриваемых в примере законов представляет собой вероятность того, что
А + B < Q.
Это неравенство выполняется для всех точек с координатами (А, В), геометрическим местом которых является область G, представляющая собой полуплоскость, лежащую ниже прямой A + B = Q (рис. 199).
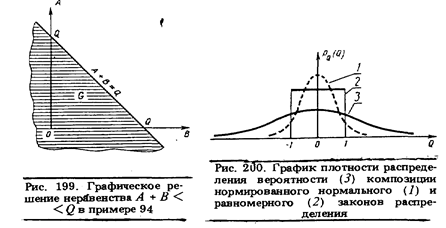
2. Выполняя в (55) интегрирование сначала по В (при постоянном А), а затем по А (или в обратном порядке), получим:
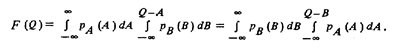
Отсюда плотность распределения вероятности суммы двух независимых результатов измерений
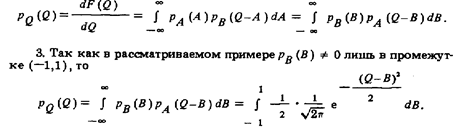
Подстановкой В = Q + v ; dB = dv последний интеграл приводится к виду:
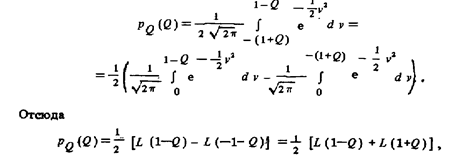
где l — функция Лапласа. График плотности распределении вероятности композиции нормированного нормального и равномерного на интервале (-1,1) законов распределения вероятности независимых результатов измерений показан на рис.200.
Любые математические операции над результатами измерений связаны с преобразованиями их законов распределения вероятности. При сложных функциях большого числа результатов измерении, это сопряжено с преодолением значительных, технических трудностей. Поэтому в таких случаях часто ограничиваются приближенными вычислениями на уровне оценок числовых характеристик.
Пусть, например,
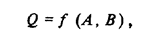
где A и B по-прежнему некоторые результаты измерений. Вводя в рассмотрение показания и поправки, можем написать:
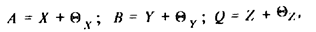
где поправки будем для простоты считать известными точно постоянными величинами, а
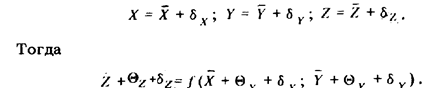
Идея приближенных вычислений состоит в том, что сложную функцию представляют рядом, в котором ограничиваются первыми членами разложения. В данном случае, считая поправки и случайные отклонения от средних значений малыми по сравнению с Х и Y, разложим функцию f в ряд Тейлора:
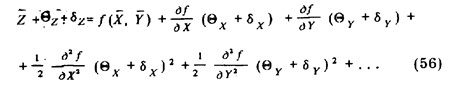
Первые слагаемые в правой и левой частях этого выражения не зависят от поправок и случайных отклонений от средних значений. Поэтому

Как обычно, вместо средних значений Х и Y могут быть использованы лишь их оценки. Это позволит получить оценку 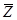 , дисперсия которой будет минимальной, если из всех возможных оценок
, дисперсия которой будет минимальной, если из всех возможных оценок 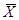 и
и 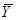 будут выбраны имеющие наименьшую дисперсию. Таковыми являются средние арифметические показаний средств измерений. Поэтому эффективная оценка
будут выбраны имеющие наименьшую дисперсию. Таковыми являются средние арифметические показаний средств измерений. Поэтому эффективная оценка 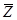 получается в результате подстановки в формулу (57)средних арифметических:
получается в результате подстановки в формулу (57)средних арифметических:
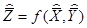 . (58)
. (58)
Для определения поправки 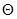 z вычтем уравнение (57) из уравнения (56):
z вычтем уравнение (57) из уравнения (56):

если только ею нельзя пренебречь. Возникновение этой поправки на неточность вычислений, объясняемое наличием квадратичных членов разложения, является важной особенностью приближенных вычислений на уровне оценок числовых характеристик.
Вычтем теперь уравнение (60) из уравнения (59), ограничившись линейными членами разложения. Получим:
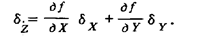
Усреднение квадрата левой и правой частей этого выражения позволяет найти приближенное значение дисперсии результата функционального преобразования:
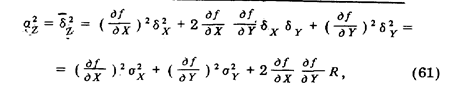
где 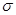 X и
X и 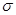 Y — средние квадратические отклонения результатов измерений A и В; R —смешанный центральный момент второго порядка совместного распределения случайных значений А и В.
Y — средние квадратические отклонения результатов измерений A и В; R —смешанный центральный момент второго порядка совместного распределения случайных значений А и В.
Общее правило образования центральных моментов совместного распределения двух случайных чисел х и у:
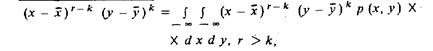
|
где r — номер или порядок момента. Смешанный момент второго порядка
 |  |
R = 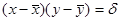 x
x 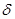 y
y
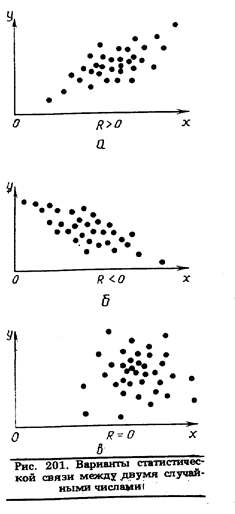
называется корреляционным и служит мерой линейной статистической связи между двумя случайными числами, которая в отличие от функциональной ука-зывает на то, что по каким-то причинам случайные числа обнаруживают тенденцию к синхрон-, ному изменению, причем не обязательно в одном направлении. Например, увеличение случайных значений х сопровождается и некоторым увеличением (рис. 201,0, или наоборот уменьшением — рис. 201, б) случайных значений у. Обычно это бывает следствием влияния какого-то общего фактора, например, изменения температуры в помещении, где проводятся измерения, или падения напряжения в сети питания и т.п. В первом случае корреляционный момент больше нуля, и говорят о положительной корреляции между случайными числами, во втором — об отрицательной корреляции. Наконец, если в значениях, прююмаемых случайными числами, не усматривается никакой статистической связи, их корреляционный момент равен нулю. Такие
случайные числа считаются независимыми— рис. 201, в. Обратное утверждение о том, что при R = 0 случайные числа или величины независимы, неверно. Так, корреляционный момент случайных величин А и Q в примере 88

 R = (A -
R = (A - 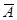 ) (Q -
) (Q - 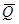 ) = A (A2 -
) = A (A2 - 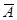 2) =
2) = 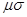 3A –
3A – 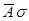 2A = 0,
2A = 0,
поскольку для симметричных распределений асимметрия 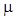 равна нулю, однако эти величины связаны между собой зависимостью Q = А2. Только в частном случае, когда случайные числа или величины подчиняются нормальному закону распределения вероятности, выполнение условия R = 0 означает их независимость.
равна нулю, однако эти величины связаны между собой зависимостью Q = А2. Только в частном случае, когда случайные числа или величины подчиняются нормальному закону распределения вероятности, выполнение условия R = 0 означает их независимость.
На практике вместо смешанного центрального момента второго порядка может быть вычислена лишь его оценка
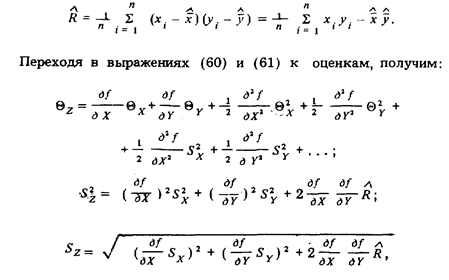
где частные производные называются функциями влияния. В случае большого числа независимых результатов измерений
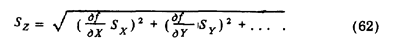
Пример 95. Найти стандартное отклонение площади квадрата в примере 93 по формуле (62).
Решение. Так как s = r1 • r2 , 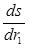 = r ;
= r ; 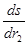 = r1. Используя вместо
= r1. Используя вместо
r1 и r2 их средние арифметические 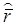 1 =
1 = 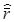 2 =
2 = 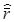 получим
получим
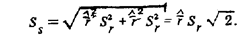
Числовые значения 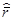 и S2r вычислены в примере84. Подставляяих, найдем
и S2r вычислены в примере84. Подставляяих, найдем
SS = 4,1 ,
что соответствует ранее полученному результату.
Пример 96. Решить пример 94 методом приближенных вычислений на уровне оценок числовых характеристик,
Решение. 1. Согласно выражению (58),
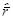 2 = 4,12 = 16,8. Поправка на неточность этого значения
2 = 4,12 = 16,8. Поправка на неточность этого значения
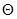 =
= 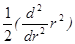 S 2r = S 2r = 0,5
S 2r = S 2r = 0,5
откуда окончательно
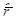 2 = 16,8 + 0,5 = 17,3 ,
2 = 16,8 + 0,5 = 17,3 ,
что соответствует результату, полученному в примере 85. 2. По формуле (62)
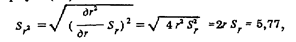
где расхождение в последнем знаке с результатом, подученным в примере 85, свидетельствует о приближенном характере вычислений.
Пример 97. С какой скоростью должно вращаться тело в примере 1, чтобы центробежная сила равнялась 2Н? Результаты измерения массы тела и радиуса окружности (в метрах) приведены в табл. 57 и 54.
Решение. 1. На основании решения примера 1

так как S 2r = 0.5 м2 ; S 2F = 0; S 2mT = 1,7 • 10- 4 кг2 . Следовательно,
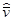 = 3, 01 м/с.
= 3, 01 м/с.
3. По формуле (62)
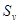
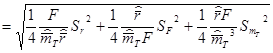 = 0.26 м/с.
= 0.26 м/с.
4. Стандартное отклонение 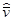
S 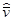 = 2,6 • 10 - 2 м/с.
= 2,6 • 10 - 2 м/с.
Поскольку закон распределения вероятности 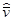 неизвестен, то на основании неравенства П.Л. Чебышева с вероятностью, большей 0,9,
неизвестен, то на основании неравенства П.Л. Чебышева с вероятностью, большей 0,9,
v = 2,9 ... 3,1 м /с.
Дата добавления: 2015-02-05; просмотров: 1188;
