Модели полупроводниковых диодов
Однопараметрическая модель Шокли описывает ВАХ идеального диода:
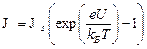 (1)
(1)
Здесь 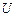 - разность потенциалов (напряжение) на выводах диода,
- разность потенциалов (напряжение) на выводах диода, 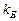 - постоянная Больцмана, Т – абсолютная температура диода. Единственный параметр
- постоянная Больцмана, Т – абсолютная температура диода. Единственный параметр 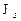 имеет смысл тока насыщения при обратном смещении диода при
имеет смысл тока насыщения при обратном смещении диода при 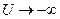 . Он равен произведению площади p-n-перехода S и плотности тока насыщения
. Он равен произведению площади p-n-перехода S и плотности тока насыщения
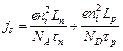 , (1а)
, (1а)
где 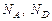 - концентрации доноров и акцепторов в p- и n-областях соответственно,
- концентрации доноров и акцепторов в p- и n-областях соответственно, 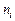 - собственная концентрация носителей,
- собственная концентрация носителей, 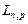 ,
, 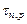 - диффузионные длины и времена жизни неосновных электронов и дырок. Модель Шокли описывает только ток инжекции.
- диффузионные длины и времена жизни неосновных электронов и дырок. Модель Шокли описывает только ток инжекции.
Если имеет место гомо p-n переход, то формулу (1а) можно модифицировать и выразить плотность тока насыщения с учетом величины ширины запрещенной зоны полупроводника:
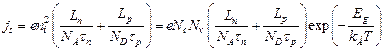
Прямая ветвь ВАХ реального диода описывается двухпараметрической зависимостью, обобщающей формулу Шокли:
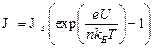 (2)
(2)
Здесь 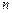 - коэффициент неидеальности диода. Он учитывает влияние на ток следующих факторов:
- коэффициент неидеальности диода. Он учитывает влияние на ток следующих факторов:
- рекомбинации носителей в области пространственного заряда (ОПЗ);
- утечек носителей;
- последовательного сопротивления базы.
Каждый из перечисленных факторов доминирует на определённых интервалах изменения токов или напряжений, поэтому коэффициент неидеальности 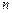 и ток насыщения
и ток насыщения 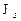 принимают на этих интервалах разные значения. В области малых токов преобладает вклад рекомбинации и утечек (при этом
принимают на этих интервалах разные значения. В области малых токов преобладает вклад рекомбинации и утечек (при этом 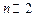 ). В области средних токов доминируют инжекционные токи и токи утечки, поэтому коэффициент неидеальности равен
). В области средних токов доминируют инжекционные токи и токи утечки, поэтому коэффициент неидеальности равен 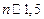 . В области больших токов, где начинает сказываться падение напряжения на последовательном сопротивлении базы, коэффициент неидеальности сначала возрастает до значений
. В области больших токов, где начинает сказываться падение напряжения на последовательном сопротивлении базы, коэффициент неидеальности сначала возрастает до значений 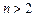 , а затем зависимость вообще меняется с экспоненциальной на степенную
, а затем зависимость вообще меняется с экспоненциальной на степенную 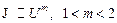 . В полулогарифмическом масштабе график прямой ветви ВАХ диода, в широком интервале токов, имеет вид, показанный на рис.1. Здесь
. В полулогарифмическом масштабе график прямой ветви ВАХ диода, в широком интервале токов, имеет вид, показанный на рис.1. Здесь 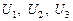 - границы упомянутых выше интервалов напряжений,
- границы упомянутых выше интервалов напряжений, 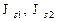 - токи насыщения на интервалах 1 и 2 соответственно.
- токи насыщения на интервалах 1 и 2 соответственно.
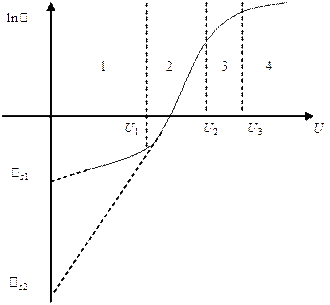
Рис. 1. ВАХ диода при прямом смещении в полулогарифмическом масштабе
Характер зависимости 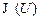 в области 4 можно установить, построив график ВАХ в логарифмическом масштабе (рис.2). Если ВАХ в области 4 удовлетворительно аппроксимируется линейной омической зависимостью
в области 4 можно установить, построив график ВАХ в логарифмическом масштабе (рис.2). Если ВАХ в области 4 удовлетворительно аппроксимируется линейной омической зависимостью
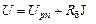 (3)
(3)
где 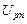 - падение напряжения на собственно p-n –переходе,
- падение напряжения на собственно p-n –переходе, 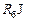 - падение напряжения на нейтральной области базы, то последовательное сопротивление этой области
- падение напряжения на нейтральной области базы, то последовательное сопротивление этой области 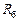 можно определить графическим дифференцированием,
можно определить графическим дифференцированием,
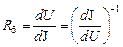
Дата добавления: 2015-01-10; просмотров: 2090;
